
- •Передмова
- •Розділ І. Лінійна та векторна алгебра
- •§1.1. Матриці, дії над матрицями
- •§1.2. Визначники
- •§1.3. Ранг матриці та способи його обчислення
- •§ 1.4. Обернена матриця
- •§1.5. Системи лінійних рівнянь
- •§1.6. Вектори
- •§1.7. Власні числа та власні вектора
- •§1.8. Квадратичні форми
- •Розділ ІІ. Аналітична геометрія
- •§2.1. Прямокутні координати в просторі. Основні задачі
- •§2.2. Пряма лінія на площині
- •§2.3. Криві лінії другого порядку
- •§ 2.4. Задачі економічного змісту
- •§ 2.5. Площина та пряма в просторі
- •§ 2.6. Нерівності та їх геометричний зміст
- •§ 2.7. Поверхні другого порядку
- •Розділ ІІІ. Вступ до математичного аналізу
- •§4.6. Деякі основні теореми диференційного числення
- •§4.7. Економічний зміст похідної. Еластичність
- •§4.8. Дослідження функцій та побудова їх графіків
- •§5.1. Основні поняття
- •§5.2. Екстремум функції двох змінних
- •§5.3. Метод найменших квадратів
- •Розділ VI. Інтегральне числення
- •§ 6.2. Методи інтегрування
- •§ 6.4. Інтегрування тригонометричних виразів
- •§ 6.5. Інтегрування виразів, що містять ірраціональність
- •§6.8. Геометричні застосування визначенних інтегралів
- •§ 6.10. Наближені обчислення визначеного інтеграла
- •§ 6.11. Невласні інтеграли. Інтеграл ЕйлераAПуассона
- •§ 6.12. Поняття про подвійний інтеграл
- •Розділ VIІ. Диференційні рівняння
- •§ 7.1. Рівняння з відокремленими змінними
- •§ 7.2. Однорідні диференційні рівняння
- •§ 7.3. Лінійне диференціальне рівняння першого порядку
- •Розділ VІІІ. Ряди
- •§ 8.2. Ознаки збіжності рядів з додатними членами
- •§ 8.3. Знакозмінні ряди. Абсолютна та умовна збіжність
- •§ 8.5. Розклад функцій в ряди Тейлора і Маклорена
- •§8.6. Застосування рядів до наближених обчислень
- •§8.7. Ряди Фур’є
- •Відповіді до задач та прикладів
- •Список використаної літератури
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
§1.6. Вектори
1.6.1. Теоретичні відомості
Вектором називається напрямлений відрізок. Напрям відрізка вказується стрілкою. Розрізняють початок і кінець вектора.
Два вектора називаються рівними між собою, якщо кожний із них можна дістати паралельним перенесенням іншого.
Рівні вектори є паралельними (колінеарними), мають один і той
самий напрям і однакову довжину. Довжина вектора a називається
абсолютною величиною або модулем вектора і позначається a .
Вектор називається нульовим (нуль,вектором), якщо він має нульову довжину, тобто його кінець збігається з початком.
Щоб знайти суму двох векторів a і b , сумістимо початок векто+
ра b з кінцем вектора a .
Сумою a + b векторів a та b називається вектор, початок
якого збігається з початком вектора a , а кінець – з кінцем вектора
b (рис. 1.1).
a + b |
a + b |
|
b |
||
b |
||
b |
b |
|
Правило трикутника |
Правило паралелограма |
|
|
Рис. 1.1. |
Для додавання векторів мають місце такі закони: 1) переставний (комутативний)
a + b = b + a ;
5 0
Розділ I. Лінійна та векторна алгебра
2) сполучний
(a + b ) + c = a + ( b + c );
3)для кожного вектора a існує протилежний (– a ), такий, що
a + (– a ) = 0 ;
4) a + 0 = a ;
5) для будь+яких двох векторів a і b виконуються нерівності:
| a + b | | a | + | b | , | a – b | | a | + | b | .
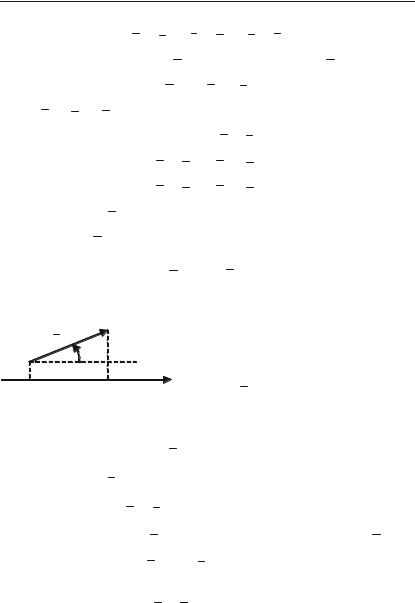
Якщо вектор a утворює кут з віссю ОХ (рис. 1.2), то проек,
цією вектора a на вісь називається величина |
|
||
|
|
прх a = ах = | a | cos , |
(1.13) |
|
|
ах = х2 – х1. |
(1.14) |
|
|
Нехай вектор має початок у точці |
|
a |
|
М1(х1, у1, z1), а кінець — |
у точці |
|
М2(х2, у2, z2). Тоді величини ах |
= х2 – х1, |
|
|
|
||
|
|
ау = у2 – у1, аz = z2 – z1 є проекціями |
|
x1 ax x2 |
X вектора a на осі х, у, z. Проекції век+ |
||
Рис. 1.2. |
тора однозначно визначають вектор. |
|
Тому має місце рівність |
||
|
a = {ах, ау, аz}.
Якщо вектор b = {bх, bу, bz}, то проекція суми векторів
a + b = {ах+bх, ау+bу, аz+bz}.
Добутком вектора a на число називається вектор a , дов+
жина якого дорівнює | a | = | || a |. Множення вектора на число має властивість асоціативності та дистрибутивності, тобто для довільних
чисел , та векторів a і b справедливі рівності:
5 1
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
1)( a ) = ( a ) = ( ) a ;
2)( ) a = a + a ;
3)( a + b ) = a + b .
Будь+який вектор a = {ах, ау, аz}. можна записати у вигляді:
|
|
|
|
|
|
|
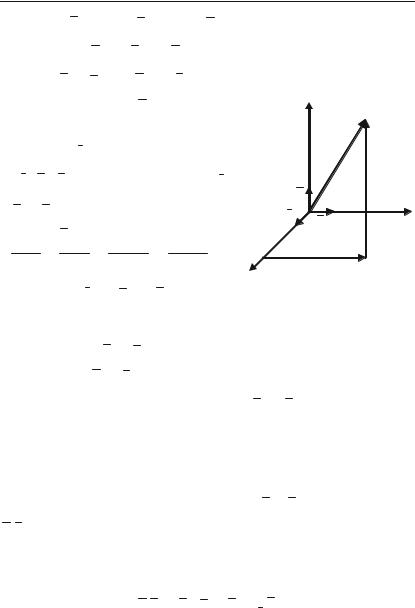
a = ах i + ау |
j |
+ аz k , |
(1.16) |
|||
де i , j , k — одиничні вектори, ах i ,
ау j , аz k називаються компонентами
вектора a (рис. 1.3).
OM1 = OM3 + M3 M2 + M2 M1 =
= ах i + ау j + аz k .
(1.15)
z  M3
M3
k
i |
j |
у |
M1
 х M2
х M2
Рис. 1.3.
Приклад 1.73. Дано два вектори: а = {2; –1; 3} та b = {3; 4; 5}.
Знайти вектор 2 a – b .
Розв’язок. 2 a – b = {2 2 – 3; 2(–1) – 4; 2 3 – 5} = {1; –6; 1}.
Ознакою колінеарності двох векторів a та b є пропорційність їх координат:
|
|
|
|
a |
|
|
ay |
|
a |
|
|
|
a b |
x |
= |
= |
z |
. |
(1.17) |
||||||
|
b |
b |
|
|||||||||
b |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
x |
|
y |
|
z |
|
|||
Скалярним добутком двох векторів a і b називається число
a b , яке дорівнює добутку їх модулів на косинус кута між ними:
a |
|
|
= | |
a |
| | |
|
| cos ( |
a |
, |
b |
). |
|
b |
b |
(1.18) |
Скалярний добуток можна записати у такому вигляді: a b = | a | b = | b | npb a .
5 2
Розділ I. Лінійна та векторна алгебра
Якщо вектори a та b задані своїми координатами, то їх скаляр+ ний добуток обчислюється за формулою:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a b = ахbx + ayby + azbz. |
|
|
(1.19) |
|||||||||
|
|
Враховуючи формули (1.18) і (1.19), можна знайти косинус кута |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
між векторами |
a |
і |
b |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ax bx ay by az bz |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
|
|
|
|
ab |
|
|
|
|
||||||||||||
|
|
cos ( a,b ) = |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
= |
|
|
|
|
|
|
|
= |
a2 |
a2 |
a2 |
b2 |
b2 |
b2 . (1.20) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
a |
b |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
y |
z |
x |
y |
z |
|
|
|
Звідси випливає умова перпендикулярності двох векторів: якщо |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
a |
b |
|
a |
|
|
= 0 або в координатній формі: |
|
|
|
|
||||||||||||||||||||||||
|
, то |
b |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ахbx + ayby + azbz = 0 . |
|
|
(1.21) |
||||||||
Серед властивостей скалярного добутку відмітимо як більш ужи+ вані такі:
1)a b = b a ;
2)a ( b + c ) = a b + a c ;
3)a b = ( a b ) = a b .
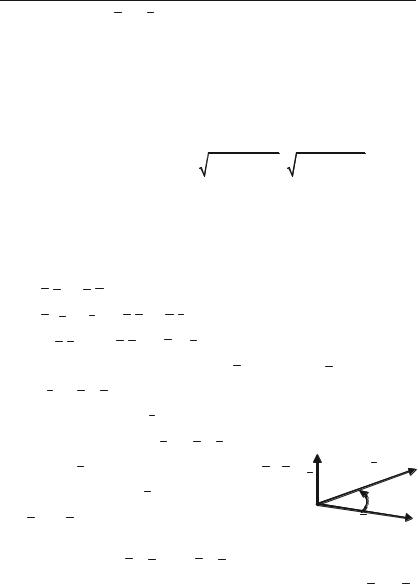
Векторним добутком вектора a на вектор b називається вектор c = a b , який має такі властивості:
1) довжина вектора c дорівнює добутку довжин співмножників на синус кута між ними: | c | = | a | | b | sin ;
2) вектор c перпендикулярний до векторів a і b ; |
b |
c |
|
3) з кінця вектора c найкоротший поворот |
|
від a до b уявлявся таким, що відбувається |
a |
проти годинникової стрілки (рис. 1.4). |
Рис. 1.4. |
|
Зауважимо, що [ a b ] = –[ a b ], а модуль векторного добутку
дорівнює площі паралелограма, побудованого на векторах a та b , якщо вони віднесені до спільного початку.
5 3

Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Укоординатній формі векторний добуток векторів a = {ах, ау, аz}
іb = {bх, bу, bz} можна записати у вигляді:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
j |
|
k |
|
|
ay |
az |
|
ax |
az |
|
ax |
ay |
|
|
|||
|
|
|
|
|
|
ax |
ay |
az |
|
|
|
|
|||||||||||||
c = a b = |
; – |
; |
|||||||||||||||||||||||
= |
|
b |
b |
b |
b |
b |
b |
|
! . (1.22) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
z |
|
|
|
|
|||
|
|
|
|
|
|
bx |
by |
bz |
|
y |
z |
|
|
|
|
x |
y |
|
" |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Мішаним або скалярно,векторним добутком трьох векторів a , b , c називається векторний добуток векторів a і b , скалярно
помножений на вектор c , тобто [ a b ] c .
Якщо вектори a , b , c — компланарні, тобто розташовані в одній площині або на паралельних площинах, то їх мішаний добуток дорів+ нює нулю.
Якщо відомі координати співмножників a = {ах, ау, аz}, b = {bх, bу, bz}, c = {сх, су, сz}, то мішаний добуток обчислюється за формулою:
|
|
|
|
|
|
|
ax |
ay |
az |
|
|
|
|
|
|
] |
|
= |
bx |
by |
bz |
. |
|
[ |
a |
b |
c |
(1.23) |
|||||||
|
|
|
|
|
|
|
cx |
cy |
cz |
|
|
Якщо три ненульових вектора a , b , c розташовані в одній пло+
щині (компланарні), то їх мішаний добуток [ a b ] c = 0.
Отже, в координатній формі умова компланарності трьох нену+
льових векторів має вигляд: |
|
|
|
|
|
|
|
|
|
|
ax |
ay |
az |
|
|
bx |
by |
bz |
= 0. |
|
cx |
cy |
cz |
|
5 4
Розділ I. Лінійна та векторна алгебра
1.6.2. Розв’язання прикладів
Приклад 1.74. Задано координати точок М1(3; 2; 1), М2(–1; 0; 2), М3(–2; –1; 0), та М4(5; 7; 3). Знайти:
1) вектор a , якщо a = 2 M1M2 – 3 M3 M4 ;
2)кут між векторами M1M2 та M3 M4 ;
3)координати вектора b = M1M2 M3 M4 ;
4)об’єм піраміди з вершинами в точках М1, М2, М3, М4.
Розв’язок.
1)За формулою (1.14) знаходимо
M1M2 = {x2 – x1; y2 – y1; z2 – z1} = {–1–3; 0–2; 2–(–1)} = {–4; –2; 3},
2 M1M2 = {–8; –4; 6},
M3 M4 = {5–(–2); 7–(–1); 3–0} = {7; 8; 3},
–3 M3 M4 = {–21; –24; –9}.
Тоді a = 2 M1M2 – 3 M3 M4 = {–8–21; –4–24; 6–9} = {–29; –28; –9}.
2) Косинус кута між векторами M1M2 та M3 M4 обчислимо за формулою (1.20):
cos = |
|
|
M1M2 |
|
|
M3 M4 |
|
|
= |
|
|
( 4) 7 ( 2) 8 3 3 |
= |
||||||
|
|
|
|
|
|
|
|
|
( 4)2 ( 2)2 32 72 82 32 |
||||||||||
|
|
|
|
M1M2 |
|
M3 M4 |
|
|
|
||||||||||
= |
|
|
28 16 9 |
|
= |
35 |
# –0,588. |
|
|||||||||||
|
4 9 |
49 64 9 |
29 |
122 |
|
||||||||||||||
16 |
|
|
|
||||||||||||||||
Оскільки косинус кута від’ємний, то кут тупий.
3) Координати векторного добутку знаходимо за формулою (1.22):
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
j |
|
k |
|
2 |
3 |
|
|
|
4 |
3 |
|
|
|
4 2 |
|
|||
|
|
4 2 3 |
|
|
|
|
|
|
|
|
||||||||||||
b = |
= i |
– |
|
|
+ k |
= |
||||||||||||||||
8 |
3 |
j |
|
|||||||||||||||||||
|
|
7 |
8 |
3 |
|
|
|
|
7 |
3 |
|
|
|
7 |
8 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 5

Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
= i (–6 – 24) – j (–12 –21) + k (–32 + 14) =
= –30 i + 33 j – 18 k = {–30; 33; –18}.
4) Щоб знайти об’єм піраміди, знайдемо спочатку мішаний добу+ ток векторів, що виходять з однієї вершини піраміди:
M1M2 = {–4; –2; 3}, M1M3 = {–5; –3; 1}, M1M4 = {4; 5; 4}. Тоді об’єм піраміди
|
1 |
|
|
|
|
|
|
|
1 |
|
4 |
2 |
3 |
|
|
19 |
|
1 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
5 |
3 |
1 |
|
= |
|
. |
||||||||
V = |
|[ |
a |
|
b |
] |
c |
| = |
= 3 |
|||||||||||||
6 |
6 |
|
|
|
6 |
6 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
4 |
5 |
4 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.6.3. Завдання для самостійної роботи
1.75. Заданими векторами a і b побудувати вектори: 1) 3 a ;
1
2) 2 a + 3 b .
1.76. Дано | a | = 13; | b | = 19; | a + b | = 24. Обчислити | a – b |.
1.77.Дано точки А(3; –1; 2) і В(–1; 2; 1). Знайти координати век+ торів AB і BA .
1.78.Дано вектори a = {2; 2; 1}, b = {6; 3; 2}. Знайти npa b , npb a .
1.79.Знайти кут між векторами a = i + 2 j + 3k , b = 6i + 4 j – 2k .
1.80.Знайти одиничний вектор того самого напрямку, що й век+
тор a = i + 2 j + 2 k .
1.81. Вектори a і b взаємно перпендикулярні, причому | a | = 5 і
|b | = 12. Знайти | a + b | і | a – b |.
1.82.Довести, що вектор p = b ( a c ) – c ( a b ) перпендикуляр+
ний до вектора a .
5 6
Розділ I. Лінійна та векторна алгебра
1.83. Дано вектори a = 3 i – 6 j – k , b = i + 4 j – 5 k , c =
=3 i – 4 j + 2 k . Обчислити npc ( a + b ).
1.84.Вектор x , компланарний вектору a = (6; –8; –7,5), утво+
рює з віссю Oz гострий кут. Знаючи, що x = 50, знайти його коор+ динати.
1.85. Знайти довжину вектора a = 20 i + 30 j – 60 k і його на+
прямні косинуси.
1.86. Дано вершини трикутника А(3; 2; –3), В(5; 1; –1) і С(1; –2; 1). Знайти його зовнішній кут при вершині А.
1.87. Вектори a і b утворюють кут = 2 3$ ; знаючи що
3$ ; знаючи що
| a | = 3, | b | = 4, обчислити: 1) (3 a – 2 b )( a + 2 b ); 2) ( a – b )2. 1.88. Дано точки А(–1; 5; –10), В(5; –7; 8), С(2; 2; –7), D(3; –2; 6).
Перевірити, що вектори AB і CD колінеарні. Знайти який з них довший і у скільки разів, як вони напрямлені — в один чи в проти+ лежні боки.
1.89. Знайти об’єм V тетраедра з вершинами А(1; 2; 3), В(4; 4; 4), С(2; 6; 4), D(2; 3; 6).
5 7
