Розділ V. Диференціальне числення функції багатьох змінних

§5.2. Екстремум функції двох змінних

Якщо функція z = f(x, y) має частинні похідні, то критичні точ+ ки, або точки підозрілі на екстремум, шукаються серед розв’язків системи:

Нехай M0(x0; y0) — критична точка. Позначимо через A, B, C відпо+ відно значення:

Якщо

1) AC B2 . 0 , то функція досягає

max z(x0; y0) при A < 0, min z(x0; y0) при A > 0;

2)AC B2 , 0 , то екстремуму немає;

3)AC B2 0 — сумнівний випадок, потрібні додаткові дос+ лідження.

Важливими є задачі на умовний екстремум, коли шукається ек+ стремум функції z = f(x; y) при умові, що змінні x та y зв’язані рівнян+

ням зв’язку (x, y) = 0.

Така задача зводиться до дослідження на безумовний екстремум функції Лагранжа L (x, y, ) .

L f (x, y) (x, y), де число називається множником Лагранжа.

Після виключення досліджуємо на екстремум функцію Лаг+ ранжа, як функцію двох змінних L(x, y).

353

Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»

5.2.1. Розв’язання прикладів

Приклад 5.50. Дослідити на екстремум функцію z x2 xy y2 9x 6y 20 .

Розв’язок. Знаходимо частинні похідні функції

дxдz 2x y 9 ,

дyдz x 2y 6 .

Розглянемо систему двох рівнянь з двома невідомими.

2x y 9 0

x 2y 6 0

Розв’язком цієї системи будуть числа x = – 4, y = 1. Точка M0(–4; 1) називається критичною.

Знаходимо частинні похідні другого порядку в точці M0.

A C B2 4 1 3 . 0

A > 0, отже існує min функції в точці (–4; 1), min z = z(–4; 1) = –1

Приклад 5.51. Дослідити на екстремум функцію двох змінних z y x y2 x 6y .

Розв’язок. Запишемо перші частинні похідні функції

дyдz x 2y 6 .

Розглянемо систему двох рівнянь з двома невідомими

354

Розділ V. Диференціальне числення функції багатьох змінних

Розв’язком цієї системи є числа x = 4, y = 4. Знаходимо другі частинні похідні функції:

Знайдемо значення других частинних похідних в точці (4, 4).

AC B2 14 161 163 . 0,

A > 0, отже існує max функції Z, max = Z(4; 4) = 12.

Приклад 5.52. Дослідити на екстремум функцію двох змінних z x3 8y3 6xy 1 .

Розв’язок. Знаходимо перші частинні похідні функції дxдz , дyдz .

Запишемо систему двох рівнянь з двома невідомими

3x2 6y 0

24y2 6x 0

Бачимо, що ця система має розв’язки

355

Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»

Знаходимо другі частинні похідні функції.

Знаходимо значення других частинних похідних в точці (0; 0). A = 0, C = 0, B = –6,

AC B2 0 36 , 0 . Перевіримо точку (1; 1/2).

A = 6, C = 24, B = –6,

24 6 36 . 0, A > 0.

Існує min функції

zmin= z(1; 1/2) = 1 + 1 – 3 + 1 = 0.

Приклад 5.53 (На умовний екстремум). Знайти екстремум функції z x2 y2 при умові x y 1 0 .

Функція Лагранжа буде мати вигляд

L (x, y, ) x2 y2 (x y 1). Запишемо необхідні умови існування екстремуму:

Критична точка буде мати координати:

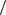M (12;1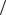2) , 1.

L(x; y) x2 y2 (x y 1) .

356

Розділ V. Диференціальне числення функції багатьох змінних

L'' 0 B ,

xy

тоді

AC B2 4 . 0, A . 0 , отже існує min функції

min z z(1/ 2;1/ 2) 1/ 4 1/ 4 1/ 2.

5.2.2. Приклади для самостійної роботи.

Дослідити на екстремум функції двох змінних.

5.54. z 800 x2 y2 40x 60y . 5.55. z 250 x2 y2 20x 100y .

5.56.z 1800 x2 y2 80x 60y .

5.57.z 2100 x2 y2 40x 100y .

5.58.z 1700 x2 y2 40x 80y .

5.59.z 1500 x2 y2 20x 80y .

5.60.z 2000 x2 y2 100x 40y .

Дослідити на умовний екстремум функції двох змінних.

357