Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Черновицкий национальный университет им. Ю. Федьковича

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Vyscha_matematyka_v_prykladakh_i_zadachakh.pdf

Скачиваний:

Добавлен:

23.02.2016

Размер:

3.55 Mб

Скачать

☆

<<< < Предыдущая 9 10 11 12 13 14 15 16 17 18 19 2021 / 4021 22 23 24 25 26 27 28 29 30 31 32 33 > Следующая >>>

Розділ V. Диференціальне числення функції багатьох змінних

§5.1. Основні поняття

Проілюструємо основні поняття і формули для функції двох змінних, оскільки перехід до більшого числа змінних не викликає ніяких труднощів. Якщо z = f(x, y), то частинні прирости за змінни+ ми х, у і повний приріст функції визначаються рівняннями:

x z = f(x + x, y) – f(x, y);y z = f(x, y + y) – f(x, y);

z = f(x + x, y + y) – f(x, y).

Якщо існує lim	x z , то ця границя називається частинною
x90	x

похідною функції z = f(x, y) за змінною х і позначається одним із символів: GGxz , zx' , fx'(x, y) , GGxf . Аналогічно визначається частинна

похідна за змінною у. Частинна похідна за однією із змінних знахо+ диться за правилами диференціювання функції однієї змінної, при+ чому друга змінна вважається при цьому сталою.

5.1.1. Розв’язання прикладів

Знайти частинні похідні функцій двох змінних.

Приклад 5.1. z = x3y – 3x2 + 2y – 1. Розв’язок.

Gx = 3х2у – 6х,

Gy = х3 + 2.

345

Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»

Приклад 5.2. z = ln(x2 – y2). Розв’язок.

x2 y2

Приклад 5.3. z = xy.

Розв’язок.

= yxy–1,

= хy ln x.

Головна лінійна відносно

х і у частина повного приросту

функції називається повним диференціалом функції, який позначається dz і обчислюється за формулою:

			Gz			Gz
dz =					dx +		dy,
dz =			Gx		dx +	Gy	dy,
Приймаючи х = dx i		y = dy знайти повний диференціал
функцій двох змінних
Приклад 5.4. z = x2 – xe y.
Розв’язок.
	Gz			= 2x – ey,
				= 2x – ey,
	Gx
		Gz			= –xey,
		Gy			= –xey,
		Gy

dz = (2x – ey)dx – xeydy.

346

Розділ V. Диференціальне числення функції багатьох змінних

Приклад 5.5. z = y .

Розв’язок.

Gz	1		,
	=
Gx		y

GGyz = yx2 ,

dz = 1y dx – yx2 dy.

Приклад 5.6. z = x 2 y.

Розв’язок.


			Gz		=	1		2y,
			Gx
						2
						2	x
		Gz			=	x 2y ln2,
		Gy			=	x 2y ln2,
		Gy
dz =	1			2ydx +				x 2y ln2dy.
dz =			x	2ydx +				x 2y ln2dy.
2			x

Частковими похідними другого порядку від функції z = f(x, y) на+ зиваються частинні похідні від її перших похідних.

	G2 z		G	Gz	,

	Gx	2
			Gx Gx
G2 z			G	Gz	,

GxGy
			Gy Gx

G2 z

Gy Gy

G2 z

GyGx

Останні дві похідні називаються мішаними і вони рівні між со+ бою за умови їх неперервності.

347

Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»

Диференціал другого порядку d2z визначається за формулою d2z = d(dz)

і обчислюється при умові неперервності мішаних похідних за фор+ мулою

G2 z

d2z =

(dx)2

+ 2

dx dy +

(dy)2.

Gx2

GxGy

Gy2

5.1.2. Приклади для самостійного розв’язання

Знайти частинні похідні

та

функції двох змінних.

5.7. z = x2 – y2.

5.9. z = tg(x – y). 5.11. z = ln(x3 – 2xy).

5.13. z = 2sin(x + y). 5.15. z = 2sin xy.

5.8. z = xy .

5.10. z = sin(x2 + y2).

5.12. z = e x– y.

5.14. z = sin x – cos y. 5.16. z = 3cos(x2y3).

Знайти повний диференціал функцій двох змінних.

5.17. z = x2y4.

5.19. z = ex – 2y. 5.21. z = x2 ln y.

5.23. z =	x y .
5.25. z =	x2 y2 .

5.18. z = 1 ln(x2 + y2).

5.20. z = sin(xy).

5.22. z = x2y – y2x.

5.24. z = tg xy .

5.26. z = x2 y2 .

Показати, що функція z = f(x, y) задовольняє рівняння.

	1 Gz	1		Gz	2
5.27. z = y ln(x2 – y2),							.
	x Gx		y	Gy		y2

348

Розділ V. Диференціальне числення функції багатьох змінних

5.28. z = x arctg

+ y

= 0.

G2 z

5.29. z = ln(x2 + y2),

= 0.

Gx2

Gy2

G2 z

5.30. z = arctg

= 0.

Gx2

Gy2

5.31. z = ln(x2 + xy + y2),

+ y

= 2.

5.32. z = x2 y2

= 1.

5.33. z = ln(e x + e y),

= 1.

G2 z

5.34. z = e xcos y,

= 0.

Gx2

Gy2

5.35. z = e xy,

G2 z

– y2

G2 z

= 0.

Gx2

Gy2

5.36. z = x ln

+ y

= z.

Похідна

функції z = f(x, y) за напрямком

(cos; , sin; )

обчислюється за формулою

cos; +

sin; ,

а обчислена в точці М(х, у) дає швидкість зміни функції в напрямку в точці М.

349

Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»

	Gz	,	Gz
Вектор				називається градієнтом функції в точці М, він

Gx			Gy

направлений в сторону найскорішої зміни функції і позначається так:

	Gz	,	Gz	Gz	i	Gz
							j .
grad z =
				Gx		Gy
Gx			Gy

Геометрично рівняння z = f(x, y) задає деяку поверхню. Щоб уявити собі вигляд поверхні перетнемо її площиною z = C (стала) і таке рівняння f(x, y) = С задає в площині хОу криву, яка в економіці називається ізоквантою. Якщо на ізокванті взяти деяку точку М(х0, у0), то вектор+градієнт в цій точці буде перпендикулярним до ізокванти.

Задача 5.37. z = x2 – xy + 2y. Знайти Gl в точці М(1; 3) в на+

	1	,	1

прямку l				.
	2		2

Розв’язок.

= 2х – у,

= 2 1 – 3 = –1,

= –x + 2,

= –1 + 2 = 1.

M =

cos; +

sin; =

–1

+ 1

= 0.

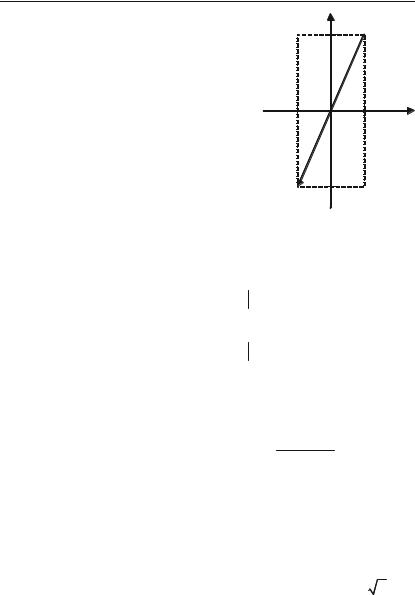
Задача 5.38.

Мі намалювати

Розв’язок.

Gx = –2х,

Нехай z = 4 – x2 – y2 і М(1; 2). Знайти grad z в точці цей вектор.

Gy = –2у,

350

Розділ V. Диференціальне числення функції багатьох змінних

M = –2,

M = –4,

grad z

M = (–2; –4)

= grad z

M .

–1

Задача 5.39. z =

, точка

–1

x2 y2

М(–1; 2). Знайти ізокванту яка прохо+

–2

дить через дану точку М і grad

x 1 .

y 2

Розв’язок.

2х,

(x2 y2 )2

2у,

(x2 y2 )2

;

grad z =

	=		8			8	,
M	=	(1	4)		2	25	,
		(1	4)			25
M	=		16	.
M	=		25	.
			25

Рівняння ізокванти в загальному вигляді (x2 y2 ) = С. Вибере+ мо С таким чином, щоб ізокванта проходила через точку М(–1; 2).

4	= С,	С =	4	,	4	=	4	,
1 4			5		x2 y2		5

тоді

х2 + у2 = 5.

Ізоквантою буде коло з центром в точці (0; 0) і радіуса 5 .

351

Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»

5.1.3. Задачі для самостійного розв’язання

Дано функцію z = f(x, y) напрямок l

та точка М0. Потрібно знай+

в точці М0 та grad z. Якщо |

| 1, то

ти похідну за напрямком

cos; =

, sin; =

2x2 2y2 ,

5.40. z = ln

, M0(1; –1).

								3		,	1
					l			3			1
5.41. z = 2x2 – 3y2,	M0(0; –2),						=					.
5.41. z = 2x2 – 3y2,	M0(0; –2),						=					.
								2			2
								2			2
									1		,	3
									1			3
5.42. z = x3 + y3 – 3xy,		M (2; 1),					l =							.
5.42. z = x3 + y3 – 3xy,		M (2; 1),					l =							.
		0							2			2
									2			2
5.43. z = 3x2 – 2xy,	M0(0; 1),				= (3; 4).
5.43. z = 3x2 – 2xy,	M0(0; 1),			l	= (3; 4).
5.44. z = x3 – y3 + x,		M (1; 1),					= (–1; 0).
5.44. z = x3 – y3 + x,		M (1; 1),				l	= (–1; 0).
		0
5.45. z = 2x3 – 3y2,	M0(2; 0),				= (0; 1).
5.45. z = 2x3 – 3y2,	M0(2; 0),		l		= (0; 1).
											1		,	1
											1			1
5.46. z = 2xy + 6x – y,		M0(2; –1), l						=							.
5.46. z = 2xy + 6x – y,		M0(2; –1), l						=			2				.
											2			2

5.47.z = x2y3 – 3x2y, M0(0; 1), l = (2; 1).

5.48.z = 5x4 – 4y3, M0(–1; 1), l = (2; 0).

5.49.z = –x2 – xy2 + 1, M0(2; 3), l = (0; –2).

352

<<< < Предыдущая 9 10 11 12 13 14 15 16 17 18 19 2021 / 4021 22 23 24 25 26 27 28 29 30 31 32 33 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.09.2019166.74 Кб2vse_razom.docx
#
18.12.2018166.05 Кб2vsi_gotovi_shpori.docx
#
03.09.2019249.86 Кб2VSTUP-1.doc
#
01.05.2019130.05 Кб19Vstup_do_psikhosomatiki.doc
#
25.11.2018205.31 Кб1Vstup_do_spec 2008.doc
#
23.02.20163.55 Mб63Vyscha_matematyka_v_prykladakh_i_zadachakh.pdf
#
20.11.2018475.14 Кб14vystavky.doc
#
23.02.2016178.81 Кб22Yatsenyuk_Petro_6 ШПОРИ.docx
#
23.02.2016783.36 Кб117Yuridichna_psikhologiya_Vidpovidi.doc
#
23.02.20161.42 Mб47Zadachni_copy.pdf
#
23.02.2016420.92 Кб140Zagalna_Psihologia-Variy.pdf