
- •Передмова
- •Розділ І. Лінійна та векторна алгебра
- •§1.1. Матриці, дії над матрицями
- •§1.2. Визначники
- •§1.3. Ранг матриці та способи його обчислення
- •§ 1.4. Обернена матриця
- •§1.5. Системи лінійних рівнянь
- •§1.6. Вектори
- •§1.7. Власні числа та власні вектора
- •§1.8. Квадратичні форми
- •Розділ ІІ. Аналітична геометрія
- •§2.1. Прямокутні координати в просторі. Основні задачі
- •§2.2. Пряма лінія на площині
- •§2.3. Криві лінії другого порядку
- •§ 2.4. Задачі економічного змісту
- •§ 2.5. Площина та пряма в просторі
- •§ 2.6. Нерівності та їх геометричний зміст
- •§ 2.7. Поверхні другого порядку
- •Розділ ІІІ. Вступ до математичного аналізу
- •§4.6. Деякі основні теореми диференційного числення
- •§4.7. Економічний зміст похідної. Еластичність
- •§4.8. Дослідження функцій та побудова їх графіків
- •§5.1. Основні поняття
- •§5.2. Екстремум функції двох змінних
- •§5.3. Метод найменших квадратів
- •Розділ VI. Інтегральне числення
- •§ 6.2. Методи інтегрування
- •§ 6.4. Інтегрування тригонометричних виразів
- •§ 6.5. Інтегрування виразів, що містять ірраціональність
- •§6.8. Геометричні застосування визначенних інтегралів
- •§ 6.10. Наближені обчислення визначеного інтеграла
- •§ 6.11. Невласні інтеграли. Інтеграл ЕйлераAПуассона
- •§ 6.12. Поняття про подвійний інтеграл
- •Розділ VIІ. Диференційні рівняння
- •§ 7.1. Рівняння з відокремленими змінними
- •§ 7.2. Однорідні диференційні рівняння
- •§ 7.3. Лінійне диференціальне рівняння першого порядку
- •Розділ VІІІ. Ряди
- •§ 8.2. Ознаки збіжності рядів з додатними членами
- •§ 8.3. Знакозмінні ряди. Абсолютна та умовна збіжність
- •§ 8.5. Розклад функцій в ряди Тейлора і Маклорена
- •§8.6. Застосування рядів до наближених обчислень
- •§8.7. Ряди Фур’є
- •Відповіді до задач та прикладів
- •Список використаної літератури
Розділ II. Аналітична геометрія
Розділ ІІ. Аналітична геометрія
§2.1. Прямокутні координати в просторі. Основні задачі
Прямокутна система координат складається із трьох взаємопер+ пендикулярних осей, що перетинаються в одній точці, які назива+ ються осями координат. Точка перетину осей називається почат, ком координат і позначається буквою О. Координатні осі позначаються через Ох, Oy i Oz і відповідно називаються віссю аб, сцис, віссю ординат і віссю аплікат.
На кожній вісі вибирається додатний напрям, що вказується стрілкою, та одиниця міри.
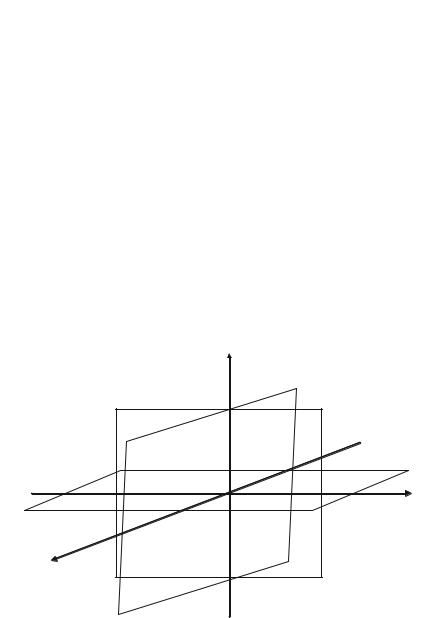
Координатні осі Ох, Oy i Oz попарно визначають площини xOy, xOz i yOz, що перетинаються в одній точці О (рис. 2.1).
Координатні площини xOy, xOz i yOz поділяють простір на вісім частин, які називаються октантами (рис. 2.1)
Z 
|
III |
|
|
II |
|
|
|
|
|
IV |
|
|
|
I |
|
|
|
|
|
|
|
|
O |
Y |
|
|
|
|
|
|
|
VII |
|
VI |
|
|
|
|
|
|
|
|
|
V |
X
VIII
Рис. 2.1.
7 9
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
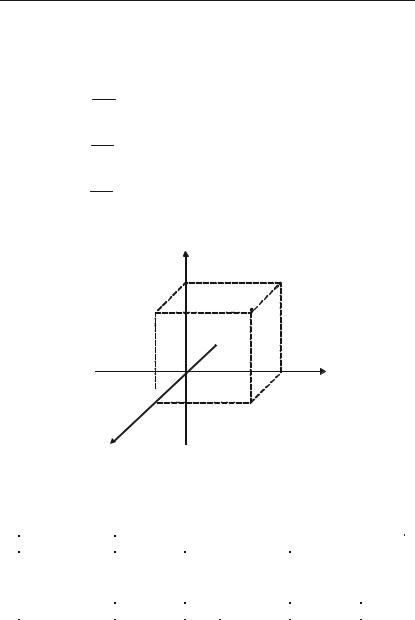
Положення точки М відносно взятих осей визначається відрізка+ ми ОА, ОВ, ОС (рис. 2.2) відповідно рівними відстаням тачки М від координатних площин. Величини цих відрізків виражаються числа+ ми, якщо виміряти їх якою+небудь одиницею міри (е).
Число x AOe — називається абсцисою точки М.
Число y OBe — називається ординатою точки М.
Число z OCe — називається аплікатою точки М.
Таким чином, положення будь+якої точки в просторі визначаєть+ ся трійкою чисел (x; y; z), які називаються її координатами.
Z
C
M |
z
|
y |
B |
|
О |
Y |
||
|
A x
x
 X
X
Рис. 2.2.
Координати точок, що розміщені в різних частинах, мають на+ ступні знаки:
Таблиця 2.1.
Координати |
|
|
|
Октанти |
|
|
|
||
І |
ІІ |
ІІІ |
ІV |
V |
VI |
VII |
VIII |
||
|
|||||||||
Абсциса |
+ |
– |
– |
+ |
+ |
– |
– |
+ |
|
Ордината |
+ |
+ |
– |
– |
+ |
+ |
– |
– |
|
Апліката |
+ |
+ |
+ |
+ |
– |
– |
– |
– |
|
8 0

Розділ II. Аналітична геометрія
Точки, що лежать на координатних площинах мають одну із ко+ ординат, яка дорівнює нулю.
Між трьома числами (x; y; z) і точками простору встановлена взаємно однозначна відповідність. Кожній трійці чисел відповідає одна і тільки одна точка простору і, навпаки, кожній точці простоA ру відповідає одна трійка чисел (x; y; z).
2.1.1. Відстань між двома точками
Якщо точки М1(x1; y1) та М2(x1; y2) належать двомірному просто+ ру R2, то відстань між двома точками визначається за формулою:
d (x |
2 |
x )2 |
(y |
2 |
y )2 . |
(2.1) |
|
1 |
|
1 |
|
Якщо ж точки М1(x1; y1; z1) та М2(x2; y2; z2) належать трьохмірно+ му простору R3, то відстань між двома точками визначається за фор+ мулою:
d (x |
2 |
x )2 |
(y |
2 |
y )2 |
(z |
2 |
z )2 . |
(2.2) |
|
1 |
|
1 |
|
1 |
|
2.1.2. Поділ відрізка в заданому відношенні
Якщо точка М(x; y; z) поділяє відрізок, що визначений точками
М1(x1; y1; z1) та М2(x2; y2; z2) в відношенні |
M1M |
|
, то її координа+ |
|||||||||
MM2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||
ти знаходяться за формулами: |
|
|
|
|
|
|
|
|
||||
x |
x1 x2 |
, |
y |
|
y1 y2 |
|
, |
z |
z1 z2 |
. (2.3) |
||
|
1 |
1 |
||||||||||
|
1 |
|
|
|
|
|
|
|||||
Увипадку, якщо точка М поділяє відрізок М1М2 навпіл, тоді l = 1,
ікоординати точки М визначаються за формулами:
x |
x1 x2 |
, |
y |
y1 y2 |
, |
z |
z1 z2 |
. |
(2.4) |
|
|
|
|||||||
2 |
|
2 |
|
2 |
|
|
|||
8 1
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
2.1.3. Площа трикутника
Площа трикутника за відомими координатами його вершин A(x1; y1), B(x2; y2), C(x3; y3) обчислюється за формулою:
S 1 ((x |
x |
2 |
)(y |
y ) (x |
2 |
x |
3 |
)(y y )). |
(2.5) |
|||
2 |
1 |
|
2 |
3 |
|
1 |
3 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
Одержане за допомогою цієї формули число необхідно взяти по |
||||||||||||
абсолютній величині. |
|
|
|
|
|
|
|
|
|
|
|
|
2.1.4. Приклади розв’язання задач |
|
|
|
|
|
|
|
|||||
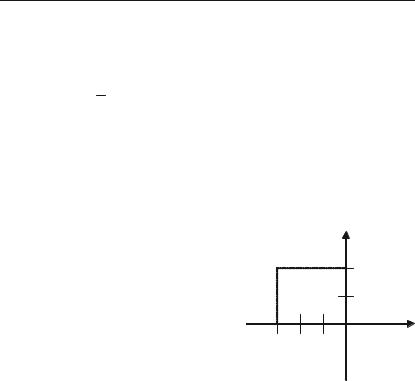
Задача 2.1. Побудувати точку С(–3; 2). |
|
|
|
|
|
|||||||
Розв’язок. Абсциса точки С дорів+ |
|
|
|
|
|
y |
|
|||||
нює –3, а її ордината 2. Виберемо оди+ |
|
С |
|
|
В |
|
||||||
|
|
|
|
|
||||||||
ницю масштабу та візьмемо на пло+ |
|
|
|
2 |
|
|||||||
щині прямокутну систему координат. |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
||||||
Відкладаємо на осі Ох вліво від почат+ |
|
|
|
|
|
|
|
|||||
ку координат О відрізок, ОА, величи+ |
|
А |
|
|
|
|
|
|||||
на якого дорівнює –3, а на осі Оy уго+ |
|
|
|
|
|
О |
x |
|||||
ру від початку координат — відрізок |
|
|
|
|
|
|||||||
ОВ, який дорівнює 2. Проводимо че+ |
–3 |
|
|
||
рез точку А перпендикуляр до осі Ох, |
|
|
а через точку В — перпендикуляр до |
Рис. 2.3. |
|
осі Оy. Перетин цих перпендикулярів |
||
|
||
і визначить точку С (рис. 2.3). |
|
Задача 2.2. Точка М(а; b) знаходиться у першому координат+ ному куті. Визначити координати точки N, яка симетрична точці М відносно бісектриси цього координатного кута.
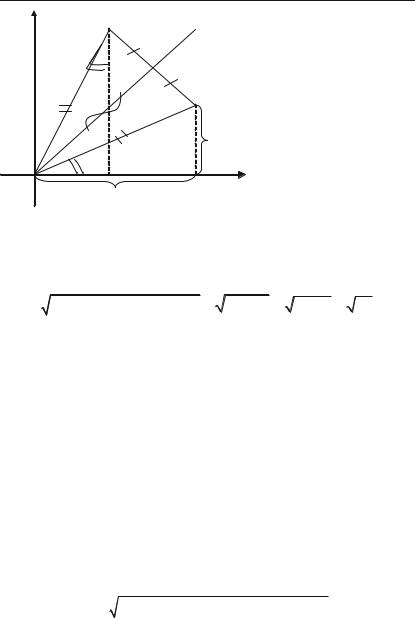
Розв’язок. Оскільки точка N симетрична точці М відносно бісект+ риси першого координатного кута, то вона лежить з точкою М на пер+ пендикулярі, який проведений до бісектриси ОР і МР = РN (рис. 2.4).
Враховуючи це, а також те, що в трикутниках OMP i OPN катет ОР – спільний, маємо, що ці прямокутні трикутники рівні між со+ бою. Розглянемо тепер трикутники ONE i OMD. Прийдемо до вис+ новку, що вони рівні, cкільки будучи прямокутними вони мають рівні гіпотенузи і рівні гострі кути MOD i ONE.
8 2
Розділ II. Аналітична геометрія
Y 
|
N |
|
|
|
P |
|
|
M |
|
|
b |
|
E |
|
O |
a |
D X |
|
Рис. 2.4. |
|
Із рівності трикут+ ників ONE i OMD маємо, що OD = NE, а MD = OE. Так як за умовою абсци+ са OD точки М дорівнює а, а її ордината MD = b то ми приходимо до виснов+ ку, що точка N має абсци+ су OE = MD = b, а орди+ нату NE = OD = a.
Отже, координатами точки N служать числа b та a: N(b; a).
Задача 2.3. Знайти відстань між точками M1(4; –5) і M2(7; –1). Розв’язок. За формулою (2.1) для відстані d між двома точками,
якщо взяти в ній x1 = 4; x2 = 7; y1 = –5; y2 = –1, одержуємо:
d (7 4)2 ( 1 ( 5))2 32 42 9 16 25 5 .
Задача 2.4. Задана точка Р(3; 5; 2). Знайти координати точки, що симетрична з точкою Р:
1) відносно початку координат;
2)відносно площини xOz;
3)відносно осі Oy.
Розв’язок.
1)Точка Р лежить в І октанті, симетрична їй точка відносно по+
чатку координат Р1 буде знаходитися в VII октанті. Її координати – Р1(–3; –5; –2).
2)Точка Р2, симетрична точці Р відносно площини xOz, буде зна+ ходитися в IV октанті, отже, її координата Р2(3; –5; 2).
3)Точка Р3, симетрична точці Р відносно осі Oy, буде знаходити+ ся в VІ октанті, отже, її координати Р3(–3; 5; –2).
Задача 2.5. Показати, що один із внутрішніх кутів трикутника А(3; 5; 3), В((2; –1; 4), С(0; –2; 1) тупий.
Розв’язок. Знайдемо довжини сторін трикутника за формулою (2.2):
d (x2 x1 )2 (y2 y1 )2 (z2 z1 )2 .
8 3
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
АВ = (2 3)2 ( 1 5)2 (3 4)2 |
1 36 1 38 ; |
|
АС = |
(0 3)2 ( 2 5)2 (1 3)2 |
9 49 4 62 ; |
ВС = |
(0 2)2 ( 2 1)2 (1 4)2 4 1 9 14 . |
|
Розглянемо співвідношення між числами, що виражають квадра+ ти сторін даного трикутника:
38 + 14 = 52, 62 > 52, 62 > 38 + 14,
тобто
АС2 > AB2 + BC2.
Отже, сторона АС лежить проти тупого кута. Кут В – тупий.
Задача 2.6. На осі Oz знайти точку, рівновіддалену від двох то+ чок М(–2; 1; 4) і N(3; 0; 1).
Розв’язок. Точка, що лежить на осі Oz має координати Р(0; 0; z). Знайдемо відстані МР і NP:
MP (0 2)2 (0 1)2 (z 4)2 4 1 (z 4)2
5 z2 8z 16 z2 8z 21;
NP |
(0 3)2 (0 0)2 (z 1)2 9 0 (z 1)2 |
|
9 z2 2z 1 z2 2z 10. |
Згідно умови, що MP = PN, одержуємо:
z2 8z 21 z2 2z 10 .
Розв’язавши одержане рівняння, знаходимо аплікату точки Р: z2 –8z + 21 = z2 –2z + 10;
–6z = –11; z = 11/6.
Р(0; 0; 11/6).
Задача 2.7. Знайти координати кінця В відрізка, якщо один кінець відрізка — точка А(–5; –7), а середина відрізка — С(–9; –12).
Розв’язок. В формулах (2.4) |
|
|
|
|
|
x |
x1 x2 |
, |
y |
y1 y2 |
, |
|
|
||||
2 |
|
2 |
|
||
8 4

Розділ II. Аналітична геометрія
координати середини відрізка позначено через x i y. За умовою за+ дачі x = –9; y = –12.
Координати одного кінця відрізка точки А в цих формулах: x1 = –5; y1 = –7. Координати відрізка точки В (другого кінця відрізка) — ве+ личини невідомі, позначені через x2 i y2.
Тоді за формулою (2.4) для визначення цих невідомих одержує+ мо два рівняння:
–9 = |
5 x2 ; |
–12 = 7 y2 . |
|
2 |
2 |
Звідси: |
|
|
–18 = –5 + x2 |
i x2 = –13; |
|
–24 = –7 + y2 |
i y2 = –17. |
|
|
В(–13; –17). |
|
Задача 2.8. Відрізок М1М2, що з’єднує точки М1(2; 5) і М2(4; 9), розділити в відношенні l = 1/3.
Розв’язок. Умова задачі вимагає знайти координати точки Р, що ділить відрізок М1М2 у відношенні l = 1/3.
Використовуючи формули (2.3), точку М1(2; 5) будемо вважати початком відрізка, а точку М2(4; 9) — його кінцем. Тоді x i y — коор+ динати точки Р, які ми шукаємо, x1 i y1 – координати точки М1, x2 i y2 — координати точки М2; l = 1/3. Отже, у нас x1 = 2; x2 = 4; y1 = 5;
y2 = 9. Маємо за формулами: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|||||||
|
2 |
|
|
|
4 |
|
|
|
2 |
|
|
|
|
|
5 |
; |
||||||||
x |
3 |
|
x |
3 |
x |
|||||||||||||||||||
1 |
|
1 |
|
|
|
|
4 |
|
|
|
|
|
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
3 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|||||||
|
|
2 |
1 |
9 |
|
|
|
|
5 3 |
|
|
|
||||||||||||
y |
|
|
|
|
|
|
||||||||||||||||||
3 |
|
y |
y 6. |
|||||||||||||||||||||
1 |
|
1 |
|
|
|
4 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
3 |
|
|
|
|
|
3 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Точка Р має координати Р(5/2; 6).
Задача 2.9. Визначити координати кінця відрізка АВ, якщо відо+ мо, що його початок в точці А(–1; 2; 4) і точка М(2; 0; 2) відтинає від нього третю частину.
8 5

Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Розв’язок. Точка М відтинає від відрізка АВ третю частину його
довжини, ділить його в відношенні l = AMMB 12 .
Використаємо формули поділу відрізка в заданому відношенні (2.3):
x |
xA xB |
|
, |
|
|
|
y |
|
|
|
yA yB |
, |
|
|
z |
|
|
zA zB |
. |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
M |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Підставивши в ці формули координати точок А і М: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
1 |
1 |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
1 |
y |
|
|
|
|
|
|
|
|
4 |
1 |
z |
|
|
|
||||||||||||||
|
|
|
|
|
B |
|
|
|
|
|
|
|
2 |
B |
|
|
|
|
|
|
B |
||||||||||||||||||||||||||||||||
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
, |
|
||||||||||||||||||
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
1 |
1 |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||||
та розв’язавши одержані рівняння, знайдемо: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
2 |
3 |
1 |
1 |
x |
|
, |
|
|
|
|
1 |
x |
|
|
4; |
|
x |
|
|
8 ; |
|
|
|
|||||||||||||||||||||||||||||
|
2 |
|
|
B |
|
2 |
B |
|
B |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
0 |
2 |
2 |
|
1 |
y |
|
|
; |
|
|
|
1 |
y |
|
2; |
|
y |
|
|
4 ; |
|
|
|
|||||||||||||||||||||||||||||
|
3 |
2 |
B |
|
|
|
2 |
B |
|
B |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
2 |
3 |
4 |
|
|
1 |
z |
|
|
; |
|
|
1 |
z |
|
|
1; |
|
z |
|
|
2. |
|
|
|
||||||||||||||||||||||||||||
|
2 |
|
|
B |
|
|
2 |
B |
|
B |
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
В(8; –4; –2).
Задача 2.10. Задано дві вершини трикутника: А(–3; –2; 2), В(4; 1; –2). Знайти третю вершину С, знаючи, що середина сторони АС лежить на осі Oy, а середина сторони ВС — на площині xOz.
Розв’язок. Позначимо середину сторони АС буквою М. Так як вона лежить на осі Oy, то її координати М(0; yM; 0). Середину сторони ВС позначимо як N, яка лежить на площині xOz, N(xN; 0; zN). Скористав+ шись формулами поділу відрізка навпіл, одержимо:
x |
|
|
xA xC |
; |
0 |
3 xC |
; |
х = 3; |
|||||
M |
|
|
|
|
|||||||||
|
|
2 |
|
|
2 |
|
|
с |
|||||
|
|
|
|
|
|
|
|
||||||
z |
|
|
|
zA zC |
; |
0 |
2 zC |
; |
z = –2; |
||||
M |
|
||||||||||||
|
|
||||||||||||
|
2 |
|
|
2 |
|
|
c |
||||||
|
|
|
|
|
|
|
|
||||||
8 6

Розділ II. Аналітична геометрія
yN |
yB yC |
; 0 |
1 yC |
; y = –1. |
|
|
|||
2 |
|
2 |
c |
|
|
|
|||
С(3; –1; 2).
2.1.5. Задачі для самостійного розв’язку
2.11.Встановити, які координати має точка симетрична точці
(–3; 5):
a) відносно осі Ох; b) відносно осі Oy;
c) відносно початку координат;
d) відносно бісектриси І та ІІІ координатних кутів; e) відносно бісектриси ІІ та IV координатних кутів.
2.12.На якій відстані від початку координат знаходяться точки: M(3; 4), N(12; –5); P(7; –24); Q(–6; –8)?
2.13.Знайдіть периметр трикутника, якщо координати його вер+ шин А(–3; –6); В(4; –1); С(5; –2).
2.14.Визначити вид трикутника якщо координати його вершин А(2; –5); В(–7; –4); С(–1; 6).
2.15.Точка, рухаючись рівномірно та прямолінійно, за 4 сек пе+ ремістилась із положення А(6; –7) в положення В(–4; 5). Де знахо+ дилась точка в момент часу 2 сек?
2.16. На осі ординат знайти точку, рівновіддалену від точок М1(1; –3; 7) і М2(5; 7; –5).
2.17. Задано три послідовні вершини паралелограма: А(1; 1); В(2; 2); С(3; –1). Знайти його четверту вершину D.
2.18.Задано дві вершини А(2; –3; –5), В(–1; 3; 2) паралелограма ABCD і точка перетину його діагоналей М(4; –1; 7). Визначити коор+ динати двох інших вершин цього паралелограма.
2.19.Задано вершини трикутника А(3; 2; –1); В(5; –4; 7) і С(–1; 1; 2). Обчислити довжину його медіани, що проведена із вер+ шини С.
2.20.Задано вершини трикутника А(1; –1; –3), В(2; –1; 3), С(–4; 7; 5). Обчислити довжину бісектриси його внутрішнього кута при вершині В.
8 7
