Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»

§2.2. Пряма лінія на площині

В прямокутній системі координат рівняння прямої на площині задається одним із наступних видів.

де k — кутовий коефіцієнт прямої, тобто тангенс того кута, який пряма утворює з додатним напрямом осі Ох, причому, цей кут відра+ ховується від осі Ох до прямої проти годинникової стрілки; b — ве+ личина відрізка, що відтинає пряма на осі ординат. При b = 0 рівнян+ ня (2.6) має вигляд y = kx, і відповідна йому пряма проходить через початок координат.

Рівняння прямої з кутовим коефіцієнтом розв’язане відносно поточної координати у.

Окремі випадки загального рівняння прямої:

а) якщо С = 0, то рівняння (2.7) буде мати вигляд:

Ах + Ву = 0, y BA x ,

якщо k BA , то y = kx, і пряма, що визначається цим рівнянням,

проходить через початок координат, так, як координати початку ко+ ординат х = 0, у = 0 задовольняють цьому рівнянню.

б) якщо в загальному рівнянні (2.7) В = 0, то рівняння матиме вигляд:

Рівняння не містить змінної у, і цим рівнянням визначається пряма, яка паралельна осі Оу.

в) якщо в загальному рівнянні (2.7) А = 0, то рівняння приймає вигляд:

8 8

Розділ II. Аналітична геометрія

Рівняння не містить змінної х, і цим рівнянням визначається пряма, яка паралельна осі Ох.

Необхідно запам’ятати, якщо пряма паралельна якій+небудь ко+ ординатній вісі, то в її рівнянні відсутній член, який містить коорди+ нату, однойменну з цією віссю.

г) При С = 0 і А = 0 — рівняння (2.7) має вигляд Ву = 0 або у = 0. Це рівняння вісі Ох.

д) При С = 0 і В = 0 рівняння (2.7) запишеться в вигляді Ах = 0

де а — величина відрізку, який відтинає пряма на вісі Ох; b — величина відрізку, який відтинає пряма на вісі Оу.

Кожний з цих відрізків відкладається від початку координат.

4. Якщо пряма має кутовий коефіцієнт k і проходить через зада+ ну точку М0(х0; у0), то її рівняння має вигляд:

Якщо в цьому рівнянні параметру k надавати різні значення, то будемо одержувати різні прямі, які проходять через задану точку (х0; у0). Тоді рівняння (2.9) дає пучок (в’язку) прямих з центром в точці М0(х0; у0).

5. Якщо пряма проходить через дві задані точки М1(х1; у1) і М2(х2; у2), то рівняння:

називається рівнянням прямої, що проходить через дві задані точки М1(х1; у1) і М2(х2; у2).

_

6. Якщо задано вектор S = {m; n}, паралельний прямій, і точку М0(х0; у0) на цій прямій, то рівняння прямої можна записати у виг+ ляді:

x x0 y y0 . m n

8 9

Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»

_

Вектор S називається напрямним вектором прямої.

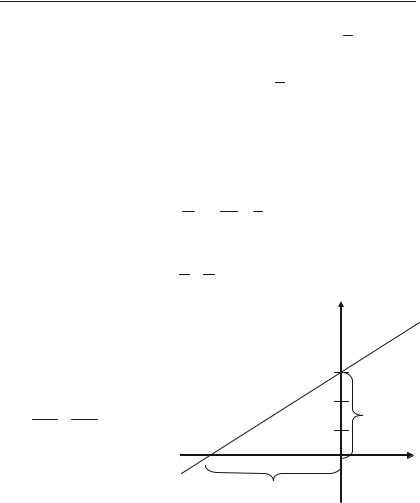
7. Кутом між прямими у = k1x + b1 і y = k2x + b2 називається кут, на який необхідно повернути пряму (з кутовим коефіцієнтом k1) до збігу її з другою прямою (з кутовим коефіцієнтом k2), проти годин+ никової стрілки.

О X

Рис. 2.5.

Необхідно звернути увагу на те, що в чисельнику дробу від куто+ вого коефіцієнта другої прямої віднімається кутовий коефіцієнт пер+ шої прямої.

Умова паралельності двох прямих:

Якщо прямі задані рівняннями в загальному вигляді:

А1х + В1у + С1 = 0 і А2х + В2у + С2 = 0,

9 0

Розділ II. Аналітична геометрія

то умовою паралельності буде рівність A1 B1 , а перпендикуляр+

A2 B2

ності є А1А2 + В1В2 = 0.

Координати точки перетину двох прямих визначаються шляхом розв’язання системи рівнянь цих прямих:

A1 x B1 y C1 0

A2 x B2 y C2 0

Відхиленням ( заданої точки М0(х0; у0) від заданої прямої Ах + Ву + С = 0 є довжина перпендикуляру, який опущено із цієї точки на пряму, взята зі знаком плюс, якщо задана точка і початок координат лежить по різні сторони від заданої прямої, і зі знаком мінус, якщо вони лежать по одну сторону від прямої.

Відхилення ( обчислюється за формулою:

( Ax0 By0 C .

) A2 B2

Відстань d від точки М0(х0; у0) до прямої Ах + Ву + С = 0 є абсолют+ на величина відхилення точки М0(х0; у0) від прямої Ах + Ву + С = 0.

A2 B2

9 1

Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»

2.2.1. Приклади розв’язання задач

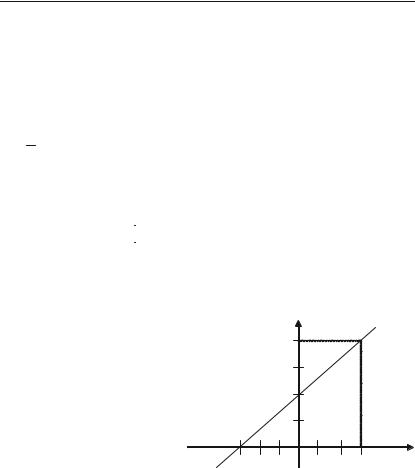
Задача 2.21. Побудувати пряму 2х – 3у + 6 = 0.

Загальний метод побудови прямої. Положення прямої на пло+ щині визначається двома точками, які належать цій прямій. Для побудови прямої досить знати координати двох довільних точок цієї прямої. Для цього обчислюємо значення у із даної рівності:

y 32 x 2 при довільних значеннях х:

при значенні х = 0, у = 2; при значенні х = 3, у = 4.

Складається наступна таблиця:

Таким чином, через одержані дві точки, координати яких В(0; 2) та А(3; 4) будуємо пряму (рис. 2.6).

Оу, має абсцису, що дорівнює 0). Тоді –3у + 6 = 0, звідти у = 2. Якщо покласти у = 0, отримаємо точку перетину прямої з віссю Ох: 2х + 6 = 0, х = –3. Позначимо одержані точки В(0; 2) і С(–3; 0).

Будуємо точки В і С та проводимо через них пряму (рис. 2.6).

Задача 2.22. Побудувати пряму 4х – у = 0.

Розв’язок. Так як вільний член рівняння дорівнює нулю, то пря+ ма проходить через початок координат. Якщо ми задамо довільне

9 2

Розділ II. Аналітична геометрія

лельна осі Оу і відтинає на осі Ох відрізок, рівний –4.

2) Аналогічно рівняння у – 3 = 0 показує, що всі точки цієї пря+ мої мають одну і ту ж ординату, тобто пряма у = 3 паралельна осі Ох і відтинає на осі Оу відрізок, рівний 3 (одиниці масштабу) (рис. 2.8).

Рис. 2.8.

Задача 2.24. Загальне рівняння прямої 3х – 4у + 12 = 0 предста+ вити у вигляді:

1)з кутовим коефіцієнтом;

2)у відрізках на осях;

3)побудувати пряму.

Розв’язок. 1) Рівняння (2.6) прямої з кутовим коефіцієнтом має вигляд y = kx + b. Щоб задане рівняння перетворити до такого

9 3

Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»

вигляду, розв’яжемо його відносно у: 4у = 3х + 12, у = 34 х + 3. Ба+

чимо, що тут кутовий коефіцієнт прямої k 34 , а величина відрізка,

що відтинає пряма на осі ординат b = 3.

Необхідно запам’ятати, якщо рівняння прямої задано в загально+ му вигляді (2.6), то кутовий коефіцієнт цієї прямої легко одержати, якщо розділити коефіцієнт при х на коефіцієнт при у і взяти одер+ жану частку з оберненим знаком:

k BA 34 34 .

2) У відрізках на осях рівняння прямої має вигляд (2.8)

Задача 2.25. Скласти рівняння прямої, що відтинає на осі Оу відрізок, рівний 4 (одиниць масштабу) та утворює з віссю Ох кут в 120о.

Розв’язок. Скористаємося рівнянням прямої з заданим кутовим коефіцієнтом у = kx + b. Згідно умові

b = 4, k = tg 120o = tg (180o – 60o) = –tg 60o = –3, k = –3.

9 4

Розділ II. Аналітична геометрія

3 (х – 1) = у + 1 3х – 3 = у + 1 3х – у – 4 = 0 (АВ).

Для знаходження рівняння сторони АС беремо А(1; –1) та С(–7; 11).

В(3; 5)

9 5

Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»

3(х – 1) = –2(у + 1) 3х – 3 = –2у – 2 3х + 2у – 1 = 0 (АС).

Для знаходження рівняння сторони ВС беремо В(3; 5) та С(–7; 11). Нехай

3(х – 3) = –5(у – 5) 3х – 9 = –5у + 25 3х + 5у – 34 = 0 (ВС).

Задача 2.27. Знайти кути та площу трикутника, сторони якого задано рівняннями: 5х – 2у – 11 = 0; х + 2у + 5 = 0; х – 2у + 1 = 0.

Розв’язок. Побудуємо заданий трикутник.

Позначимо його вершини буквами А, В, С. Рівняння першої сто+ рони АВ є х – 2у + 1 = 0. Кутовий коефіцієнт прямої АВ

kAB = BA = 12 = 12 .

Рис. 2.11.

9 6

Розділ II. Аналітична геометрія

Рівняння прямої ВС є х + 2у + 5 = 0. Кутовий коефіцієнт пря+ мої ВС

kВС = BA = 12 .

Рівняння прямої АС є 5х – 2у – 1 = 0. Кутовий коефіцієнт пря+ мої АС

kВС = BA = 52 52 .

Кути трикутника будемо знаходити за формулою (2.11)

*A arctg 89 .

*B arctg 43 .

*C arctg12 .

9 7

Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»

Для того щоб знайти площу трикутника, необхідно визначити координати його вершин. Точки А, В і С ми знайдемо, розв’язавши системи рівнянь прямих, що дають ці прямі в перетині.

Розв’яжемо систему:

5x 2y 11 0

а) x 2y 5 0

Додамо до першого рівняння друге:

5х – 2у – 11 + х + 2у + 5 = 0 + 0; 6х – 6 = 0; 6х = 6; х = 1.

Підставимо отримане значення змінної х в будь+яке рівняння системи, наприклад в друге:

1 + 2у + 5 = 0; 6 + 2у = 0; 2у = –6; у = –3.

Отримали точку С(1; –3).

5x 2y 11 0

б) x 2y 1 0

Віднімемо від першого рівняння друге:

5х – 2у – 11 – х – (–2у) – 1 = 0 – 0; 4х – 2у + 2у – 12 = 0; 4х = 12; х = 3.

Підставимо отримане значення змінної х у будь+яке рівняння, наприклад у друге:

3 – 2у + 1 = 0; 4 – 2у = 0; 4 = 2у; у = 2.

Отримали точку А(3; 2).

x 2y 5 0 в) x 2y 1 0

Додамо до першого рівняння друге:

х + 2у + 5 + х – 2у + 1 = 0 + 0; 2х + 6 = 0; 2х = –6; х = –3.

Підставимо отримане значення змінної х у будь+яке рівняння, наприклад у друге:

–3 –2у + 1 = 0; –2у = 2; у = –1. Отримали точку В(–3; –1).

9 8

Розділ II. Аналітична геометрія

Знайдемо площину трикутника за формулою:

1

S = 2 (x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2));

S = 12 (3(–1+3) – 3(–3 – 2) + 1(2 + 1)) = 12 (6 + 15 + 3) = 12 24 = 12.

Площа трикутника S = 12 кв. од.

Задача 2.28. Знайти рівняння прямої, що проходить через точку М0(2; 5) паралельно прямій 3х – 4у + 15 = 0.

Розв’язок. Виходячи з того, що шукана пряма паралельна заданій, її кутовий коефіцієнт дорівнює кутовому коефіцієнту заданої пря+ мої, тобто k1 = k2 = k.

k1 = BA 34 34 = k2 = k.

Складемо рівняння шуканої прямої за формулою:

у– у0 = k(х – х0);

у– 5 = 34 (х – 2);

4у – 20 = 3х – 6; 3х – 4у + 14 = 0.

Шукане рівняння прямої 3х – 4у + 14 = 0.

Задача 2.29. Знайти рівняння прямої, що проходить через точку Р0(5; –1) і перпендикулярна до прямої 3х – 7у + 14 = 0.

Розв’язок. Так як шукана пряма перпендикулярна заданій, то до+ буток кутових коефіцієнтів обох прямих має дорівнювати –1, тобто k1k2 = –1. Таким чином, кутовий коефіцієнт шуканої прямої має бути обернений за абсолютною величиною і протилежний за знаком ку+ товому коефіцієнту заданої прямої:

k2 1 . k1

Знайдемо кутовий коефіцієнт заданої прямої:

k1 BA 37 73 .

9 9

Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»

За умовою перпендикулярності:

Знаходимо рівняння шуканої прямої за формулою:

у– у0 = k(х – х0),

у+ 1 = 73 (х – 5),

3(у + 1) = –7(х – 5), 3у + 3 = –7х + 35,

7х + 3у – 32 = 0. Шукане рівняння прямої: 7х + 3у – 32 = 0.

Задача 2.30. Знайти проекцію точки М(–8; 12) на пряму, що проходить через точки С(2; –3) та D(–5; 1).

Розв’язок. Рівняння прямої СD знайдемо за формулою (2.10):

4(х – 2) = –7(у + 3), 4х – 8 = –7у – 21, 4х + 7y + 13 = 0.

Проекцією точки М на пряму СD буде основа перпендикуляра, який опущений із точки М на пряму СD. Рівняння перпендикуляра MN можна знайти за формулою у – у0 = k(х – х0), так як координати точки М задано, а кутовий коефіцієнт, згідно умові перпендикуляр+ ності дорівнює:

у – 12 = 74 (х + 8);

100

Розділ II. Аналітична геометрія

7х – 4у + 104 = 0.

Одержали рівняння 7х – 4у + 104 = 0 перпендикуляра MN. Розв’язавши систему рівнянь MN i CD знайдемо проекцію точки

М на пряму CD.

Використовуючи формули (2.14) знаходимо х та у: x x 65780 12 ;

y y 32565 5 . Шукана точка N(–12; 5).

Задача 2.31. Знайти відстань між двома паралельними прями+

ми:

3х + 4у – 12 = 0 3х + 4у + 13 = 0.

Розв’язок. Шукану відстань ми знайдемо як відстань від довіль+ ної точки однієї прямої до другої прямої. Візьмемо на першій прямій довільну точку, наприклад точку з абсцисою х = –4, її ордината буде:

3(–4) + 4у – 12 = 0; 4у = 24; у = 6.

Отже, на першій прямій вибрана точка М0(–4; 6). Знайдемо відстань від точки М0(х0; у0) до заданої другої прямої Ах + Ву + С = 0 за формулою (2.15):

101

Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»

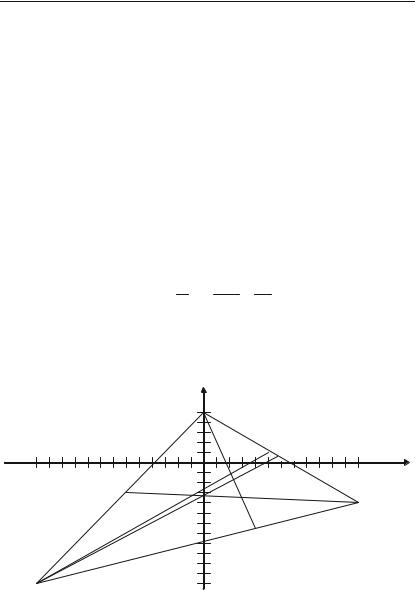
Задача 2.32. Задано вершини трикутника А(12; 4), В(0; 5), С(–12; –11). Знайти:

1)довжини сторін;

2)рівняння сторін;

3)рівняння висоти, що проведена з вершини В;

4)довжину цієї висоти;

5)рівняння медіани, що проведена із вершини А;

6)точку перетину висоти, що проведена із вершини В, та медіа+ ни, що проведена з точки А;

7)рівняння бісектриси кута С;

8)центр ваги трикутника;

9)кут С;

10)площу трикутника.

Розв’язок.

1) Довжини сторін визначимо за допомогою формули відстані між двома точками:

d (x1 x2 )2 (y1 y2 )2 ;

2) Кожна сторона трикутника проходить через дві точки, через це для знаходження рівнянь сторін використаємо формулу (2.10):

Знайдемо рівняння сторін:

102

Розділ II. Аналітична геометрія

7(х – 12) = 24(у + 4) = 0 7х – 84 = 24у + 96

7х – 24у – 180 = 0 (АС).

2)Щоб скласти рівняння висоти, яка проведена із точки В на сторону АС, необхідно знати кутовий коефіцієнт висоти.

Спочатку знайдемо кутовий коефіцієнт сторони АС

k1 BA 724 247 .

З умови перпендикулярності двох прямих k1 k2 1 знайдемо кутовий коефіцієнт висоти BD:

Y

В

Рис. 2.12.

103

Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»

Складемо рівняння висоти, скориставшись формулою:

у – у0 = k(х – х0),

у– 5 = 247 (х – 0),

7у – 35 = –24х, 24х + 7у – 35 = 0 (BD).

4) Для знаходження довжини BD використаємо формулу (2.15):

d Ax0 By0 C , A2 B2

за допомогою якої знайдемо відстань від точки В(5; 0) до прямої АС 7х – 24у – 180 = 0 (АС)

5) Для знаходження рівняння медіани АМ потрібно знайти коор+ динати точки М.

Координати точки М(–6; –3).

Рівняння медіани АМ знаходиться як рівняння прямої, що про+ ходить через дві точки А(12; –4) та М(–6; –3).

х –12 = –18у – 72 х + 18у + 60 = 0 (АМ).

6)Щоб знайти координати точки F перетину висоти BD та меді+ ани AM, необхідно розв’язати систему рівнянь цих прямих:

104

Розділ II. Аналітична геометрія

24x 7y 35 0

x 18y 60 0

247

1 18 = 432 –7 = 425;

357

x 60 18 = 630 + 420 = 1050;

2435

x 1 60 = –1440 – 35 = –1475;

x x 1050425 # 2,47 ;

y y 4251475 # 3,47.

Шукана точка перетину F(2,47; –3,47).

7) Для знаходження рівняння бісектриси внутрішнього кута С необхідно знайти координати точки K. Згідно властивості бісектри+ си внутрішнього кута трикутника, яка ділить сторону АВ в відно+

шенні AKKB CBAC , знаходимо CBAC 1520 54 . Знаходимо ко+ ординати точки K за формулами:

105

Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»

Шукана точка K( 163 ; 1).

Знаходимо рівняння бісектриси внутрішнього кути С:

3(x 12) y 11 9(х + 12) = 13(у + 11)

13 3

9х + 108 = 13у + 143 9х – 13у – 35 = 0 (СК).

8)Центр ваги трикутника Е визначається за формулами:

Величина кута *C arctg 34 .

106

Розділ II. Аналітична геометрія

10) Знайдемо площу трикутника за формулою:

1

S = 2 dAC dBD;

S = 12 25 12 = 25 6 = 150. Шукана площа S = 150 (кв. од.).

2.2.2. Задачі для самостійного розв’язку

2.33.Які з точок М(3; 5), N(2; 7), P(–1; –3), Q(–2; 0), R(3; –5) лежать на прямій у = 2х – 1, а які лежать вище або нижче цієї прямої?

2.34.Задана пряма 2х + 3у + 4 = 0. Скласти рівняння прямої, що проходить через точку М(2; 1):

1) паралельно заданій прямій;

2) перпендикулярно до заданої прямої.

2.35.Знайти проекцію точки Р(–6; 4) на пряму 4х – 5у + 3 = 0.

2.36.Знайти точку Q, яка симетрична точці Р(–5; 13) відносно прямої 2х – 3у – 3 = 0.

2.37.Знайти точку М1, яка симетрична точці М2(8; –9) відносно прямої, що проходить через точки А(3; –4) і В(–1; –2).

2.38.Задано вершини трикутника А(1; –1), В(–2; 1) і С(3; 5). Скласти рівняння перпендикуляра, що опущений із вершини А на медіану, яка проведена із вершини В.

2.39.Задано вершини трикутника А(2; –2), В(3; –5) і С(5; 1). Скласти рівняння перпендикуляра, який опушений із вершини С на бісектрису внутрішнього кута при вершині В.

2.40.Задано дві суміжні вершини А(2; 5) і В(5; 3) паралелограма ABCD і точка М(–2; 0) перетину його діагоналей. Скласти рівняння сторін цього паралелограма.

2.41.Задано рівняння двох суміжних сторін паралелограма

х– у –1= 0 і х – 2у = 0 та точка перетину його діагоналей М(3; –1). Скласти рівняння двох інших сторін паралелограма.

2.42.В рівнобедреному прямокутному трикутнику задано коор+ динати вершини гострого кута (5; 7) і рівняння його протилежного

107

Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»

катета 6х + 4у – 9 = 0. Скласти рівняння двох інших сторін трикут+ ника.

2.43.Знайти вершини прямокутного рівнобедреного трикутника, якщо задано вершина прямого кута С(3; –1) та рівняння його гіпоте+ нузи 3х – у + 2 = 0.

2.44.Точка А(2; –5) є вершиною квадрата, одна із сторін якого лежить на прямій х – 2у – 7 = 0. Обчислити площу цього квадрату.

2.45.Задано вершини трикутника А(–10; –13), В(–2; 3) і С(2; 1). Обчислити довжину перпендикуляра, який опущений із вершини В на медіану, що проведена із вершини С.

2.46.Сторони АВ і ВС паралелограма задано рівняннями 2х – у + 5 = 0 і х – 2у + 4 = 0, діагоналі його перетинаються в точці М(1; 4). Знайти довжину його висот.

2.47.Задано дві вершини трикутника А(–4; 3) і В(4; –1) і точка перетину його висот М(3; 3). Знайти третю вершину С.

2.48.В трикутнику АВС відомо: сторона АВ: 4х + у – 12 = 0, висота ВK: 5х – 4у – 15 = 0 і висота АН: 2х + 2у – 9 = 0. Скласти рівняння двох інших сторін трикутника і третьої висоти.

2.49.Скласти рівняння сторін трикутника, знаючи одну із його вер+ шин А(3; –4) та рівняння двох висот 7х – 2у – 1 = 0 і 2х – 7у – 6 = 0.

2.50.Задана пряма 2х + у – 6 = 0 і на цій прямій дві точки А і В ординатами уА = 6 і уВ = –2. Знайти рівняння висоти АD трикутника

АОВ, знайти її довжину і *DAB .

108