Розділ II. Аналітична геометрія

§2.3. Криві лінії другого порядку

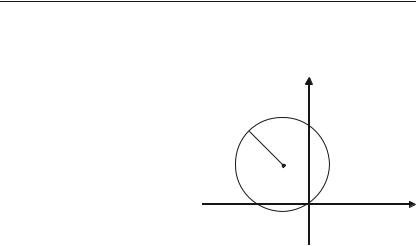
2.3.1. Коло

Коло — рівняння другого порядку. Загальне рівняння кривої другого порядку:

Ах2 + 2Вху + Су2 + Dx + Ey + F = 0

являє собою коло, якщо коефіцієнти при квадратах координат рівні між собою А = С, і якщо відсутній член з добутком координат ху, тобто В = 0.

2.3.2. Еліпс

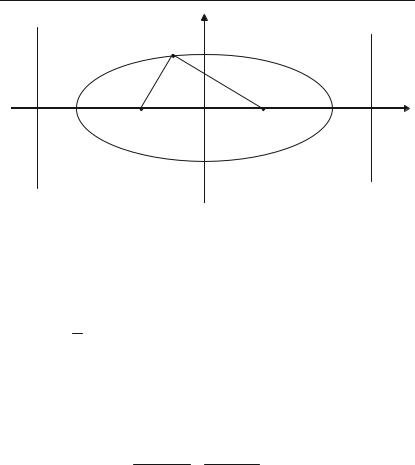
Еліпсом називається геометричне місце точок, сума відстаней яких до двох фіксованих точок, що називаються фокусами, є величина ста+ ла і дорівнює 2а (рис. 2.14). Канонічне рівняння еліпса має вигляд:

Координати фокусів еліпса F1(c; 0) i F2(–c; 0). Відстань між фоку+ сами дорівнює 2с. Точки перетину еліпса з осями координат А1(а; 0), А2(–а; 0) і В1(0; b), B2(0; –b) — називаються вершинами еліпса.

Відрізки А1А2 = 2а, В1В2 = 2b — називаються осями еліпса.

109

Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»

Відстані r1 та r2 точки М(х; у) еліпса до його фокусів називаються фокальними радіусами цієї точки і визначаються за формулами:

r1 = а – eх, r2 = а + eх.

Дві прямі, які паралельні до малої осі еліпса і знаходяться від неї

на відстані a , називаються директрисами еліпса. Їхні рівняння: e

Рівняння еліпса с осями, що паралельні координатним осям, має вигляд:

(x x0 )2 (y y0 )2 1, a2 b2

де (х0; у0) — координати центра еліпса.

2.3.3. Гіпербола

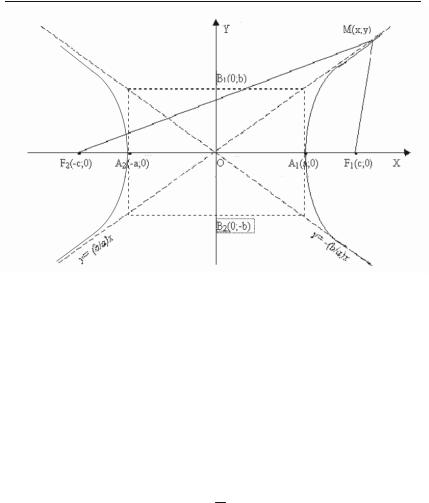
Гіперболою називається геометричне місце точок, для кожної із яких абсолютне значення різниці відстаней до двох заданих точок, що називаються фокусами, є величина стала і дорівнює 2а (рис. 2.15).

Канонічне рівняння гіперболи має вигляд:

110

Розділ II. Аналітична геометрія

Рис. 2.15.

Координати фокусів гіперболи F1(c; 0) i F2(–c; 0). Відстань між фокусами дорівнює 2с.

Точки перетину гіперболи з віссю абсцис А1(а; 0), А2(–а; 0) нази+ ваються дійсними вершинами. Відстань А1А2 = 2а називається дійсною віссю гіперболи.

Точки В1(0; b), B2(0; –b) називаються уявними вершинами, а відрізок В1В2 = 2b — уявною віссю гіперболи.

Ексцентриситет гіперболи e ac . 1.

Відстані r1 та r2 точки М(х; у) гіперболи до його фокусів назива+ ються фокальними радіусами цієї точки і визначаються за форму+ лами:

r1 = eх – а, r2 = eх + а,

за умови, що точка М(х; у) лежить на правій вітці гіперболи.

111

Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»

Дві прямі, які паралельні уявній осі гіперболи і знаходяться від неї

на відстані a називаються директрисами гіперболи. Їхні рівняння: e

x a2 , x a2 . c c

Прямі, які визначаються рівняннями:

y ab x , y ab x , називаються асимптотами гіперболи.

Дві гіперболи, що задані рівняннями:

називаються спряженими. Вони мають спільні асимптоти.

Якщо вісі гіперболи рівні, тобто а = b, то гіпербола називається

рівнобічною, або рівносторонньою. Її рівняння має вигляд: х2 – у2 = а2.

Її асимптотами служать бісектриси координатних кутів.

Якщо за вісі координат прийняти асимптоти рівносторонньої гіперболи, то її рівняння приймає вигляд:

ху = k, де k a2 .

2

2.3.4. Парабола

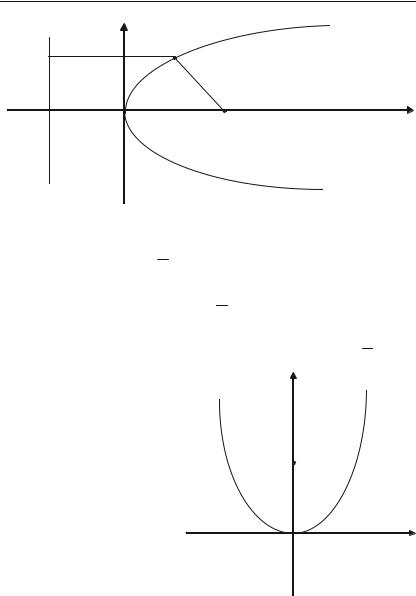
Параболою називається геометричне місце точок рівновіддале+ них від заданої точки — фокуса та заданої прямої — директриси (рис. 2.16).

Канонічне рівняння параболи має вигляд:

де р — відстань від фокуса до директриси. Вершина параболи знахо+ диться в початку координат, віссю симетрії є вісь абсцис.

112

Розділ II. Аналітична геометрія

Рис. 2.16.

Координати фокуса F( 2p ; 0). Рівняння директриси DN має вигляд:

113

Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»

Рівняння параболи з віссю симетрії, яка паралельна одній із ко+ ординатних осей, має вигляд:

(у – у0)2 = 2р(х – х0),

або

(х – х0)2 = 2q(у – у0), де (х0; у0) — координати вершин параболи.

2.3.5. Приклади розв’язання задач

Задача 2.51. Скласти рівняння кола з центром в точці С(2; –3) і радіусом, що дорівнює 6.

Розв’язок. В рівнянні (2.16) (х – а)2 + (у – b)2 = r2 маємо а = 2; b = –3; r = 6. Зразу одержимо:

(х – 2)2 + (у + 3)2 = 36.

Задача 2.52. Визначити центр і радіус кола, яке задано рівнянням:

х2 + у2 – 2х + 4у – 20 = 0.

Розв’язок. Так як в заданому рівнянні коефіцієнт при х2 і у2 рівня між собою і відсутній член з добутком координат, то задане рівнян+ ня є рівнянням кола. Його необхідно привести до вигляду (2.16). Випишемо члени, які містять тільки х, і члени, які містять тільки у. Виділимо повний квадрат:

х2 – 2х = х2 – 2х+1 + 12 – 12 = (х – 1)2 – 1, у2 + 4у = у2 + 2у+ 2 + 22 – 22 = (у + 2)2 – 4.

Ліва частина заданого рівняння запишеться так:

(x 1)2 1 (y 2)2 4 20 0

x2 2x y2 4y

звідки: (х – 1)2 + (у + 2)2 = 25.

Порівнюючи одержане рівняння з рівнянням (2.16) приходимо до висновку, що це рівняння визначає коло, центр якого має коорди+ нати С(1; –2), r2 = 25, а r = 5.

Задача 2.53. Скласти рівняння кола, що проходить через точки М1(–1; 1) і М2(1; –3), якщо центр його лежить на прямій 2х – у +1 = 0.

Рішення. Канонічне рівняння кола:

(х – а)2 + (у – b)2 = r2.

114

Розділ II. Аналітична геометрія

Так як коло проходить через точки М1(–1; 1) і М2(1; –3), то ко+ ординати цих точок повинні задовольняти рівнянню кола. Звідти маємо два рівняння:

(–1 – а)2 + (1 – b)2 = r2, (1 – а)2 + (–3 – b)2 = r2.

Якщо центр кола знаходиться на прямій 2х – у + 1 = 0, то коор+ динати центра повинні задовольняти рівнянню прямої. Одержуємо трете рівняння:

2а – b + 1 = 0.

Розв’яжемо систему рівнянь:

115

Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»

Щоб визначити r2, скористаємося рівнянням: r2 = (–1 – а)2 + (1 – b)2;

Задача 2.54. Скласти рівняння кола, що проходить через три задані точки: М1(–1; 5), М2(–2; 2) і М3(5; 5).

Розв’язок. Шукане рівняння має вигляд: (х – а)2 + (у – b)2 = r2. Так як коло проходить через задані точки, то координати кожної з цих точок задовольняють рівнянню кола.

Підставляємо по черзі в шукане рівняння координати заданих точок, одержимо три рівняння для визначення а, b i r.

Від першого рівняння віднімемо друге, а потім від першого рівнян+ ня віднімемо трете. Одержуємо систему двох рівнянь з двома невідо+ мими:

Звідки а = 2, b = 1.

Для знаходження r2 скористаємося точкою М1(–1; 5) і рівнянням:

r2 = (х – а)2 + (у – b)2.

r2 = (–1 – 2)2 + (5 – 1)2 = 9 + 16 = 25. Шукане рівняння кола моє вигляд:

(х –2)2 + (у – 1)2 = 25.

Задача 2.55. Знайти довжину осей, координати фокусів і екс+ центриситет еліпса 4х2 + 9у2 = 144.

116

Розділ II. Аналітична геометрія

Розв’язок. Приведемо це рівняння до канонічного вигляду (2.17):

x2 y2 1 . a2 b2

Розділивши обидві частини заданого рівняння на 144, одержимо:

x2 y2 1.

36 16

Звідти одержуємо, що а2 = 36, b2 = 16. Отже а = 6, 2а = 12; b = 4, 2b = 8. Знаючи а і b, із співвідношення а2 – с2 = b2 знаходимо с:

с2 = а2 – b2 = 36 – 16 = 20, c 20 2 5 .

Координати фокусів будуть: F1( 2 5 ; 0) і F2( 2 5 ; 0).

Ексцентриситет еліпса - ac 265 35 .

Задача 2.56. Велика вісь еліпса дорівнює 8, а відстань між ди+ ректрисами дорівнює 16. Знайти рівняння еліпса. Чому дорівнює його ексцентриситет?

Розв’язок. Для знаходження рівняння еліпса необхідно знайти його піввісі а ти b. За умовою 2а = 8, а = 4.

Піввісь b знаходимо із співвідношення b2 = а2 – с2, а с можна знайти, використовуючи відстань між директрисами

Одержуємо рівняння еліпса: x2 y2 1.

16 12

Ексцентриситет еліпса e ac 42 12 .

117

Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»

Задача 2.57. Скласти рівняння гіперболи, фокуси якої знаходять+ ся на осі абсцис, симетрично відносно початку координат, якщо за+

обхідно знайти її піввісі а та b. Скористуємося умовою: точка

М ( 9 ; –1) знаходиться на гіперболі, а це означає, що координати

1 2

точки М1 повинні задовольняти рівнянню гіперболи:

118

Розділ II. Аналітична геометрія

Підставимо отримані значення параметрів в канонічне рівняння гіперболи:

Таким чином, отримуємо шукане рівняння гіперболи:

x2 y2 1.

18 8

Задача 2.58. Знайти канонічне рівняння гіперболи, якщо кут між

її асимптотами дорівнює 120о і відстань між фокусами дорівнює 8 3 . Розв’язок. Канонічне рівняння гіперболи має вигляд:

x2 y2 1. a2 b2

Рівняння асимптот y ) ab x , де ab tg , а – кут нахилу асимптоти до осі Ох.

Так як кут між асимптотами дорівнює 120о, то 1202 60 .

с2 = а2 + b2 одержуємо друге рівняння:

( 4 3 )2 = а2 + b2.

119

Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»

Отримуємо рівняння:

x2 y2 1.

12 36

Задача 2.59. Скласти рівняння параболи, знаючи, що парабола симетрична відносно осі Ох, проходить через точку М(1; –4) і поча+ ток координат.

Розв’язок. Канонічне рівняння параболи, що симетрична віднос+ но осі Ох, вершина якої знаходиться в початку координат є у2 = 2рх. Для складання рівняння необхідно знайти значення параметра р. Так як парабола проходить через точку М(1; –4), то координати цієї точ+ ки задовольняють рівнянню параболи:

(–4)2 = 2р 1, 16 = 2р, р = 8.

Звідси у2 = 16х.

Задача 2.60. Обчислити довжину сторін правильного трикутни+ ка, який вписаний в параболу у2 = 2рх.

Розв’язок. Трикутник АОВ розміщений симетрично відносно осі параболи. Одна із його вершин співпадає з вершиною параболи, а протилежна сторона — перпендикуляр до осі параболи (рис. 2.18).

За умовою задачі AOB рівносторонній. Кут *AOB 60 , то *AOD 30 . Нехай координати точки А(х; у). З DOA маємо

120

Розділ II. Аналітична геометрія

2.3.6. Задачі для самостійного розв’язку

2.61. Скласти рівняння кола, що проходить через точку М(2; 6) і його центр співпадає з точкою С(–1; 2).

2.62. Скласти рівняння кола, якщо мочки А(3; 2) і В(–1; 6) явля+ ються кінцями одного із діаметрів кола.

2.63. Скласти рівняння кола, центр якого співпадає з точкою С(1; –1) і пряма 5х – 12у + 9 = 0 являється дотичною до кола.

2.64. Скласти рівняння кола, що проходить через точки А(3; 1) і В(–1; 3), а його центр лежить на прямій 3х – у – 2 = 0.

2.65. Скласти рівняння кола, що проходить через точки А(1; 1), В(1; –1) і С(2; 0).

2.66. Скласти рівняння еліпса, фокуси якого розміщені на осі абсцис симетрично відносно початку координат. Знаючи, що:

1)його велика вісь дорівнює 10, а відстань між фокусами 2с = 8;

2)його мала вісь дорівнює 24, а відстань між фокусами 2с = 10;

3)відстань між його фокусами 2с = 6 і ексцентриситет e 35 ;

4)його велика вісь дорівнює 20, а ексцентриситет e 35 ;

5)його мала вісь дорівнює 10, а ексцентриситет e 1312 .

121

Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»

2.67. Скласти рівняння еліпса, фокуси якого розміщені на осі абсцис симетрично відносно початку координат, якщо задано:

1)точка М1( 2 5 ; 2) і його мала піввісь b = 3;

2)точка М1(2; –2) і його велика піввісь а = 4;

3)точки М1(4; 3 ) і М2( 2 2 ; 3) еліпса;

4) точка М1( 15 ; –1) еліпса і відстань між його фокусами 2с = 8; 5) точка М1(2; 53 ) еліпса і його ексцентриситет e 32 .

2.68. Знайти ексцентриситет еліпса, знаючи, що:

1) малу вісь його видно із фокуса під прямим кутом; 2) відстань між фокусами дорівнює відстані між вершинами малої

та великої осей.

2.69. Скласти рівняння гіперболи, фокуси якої розміщені на осі абсцис симетрично відносно початку координат, знаючи, що:

1)відстань між фокусами 2с = 10 і вісь 2b = 8;

2)відстань між фокусами 2с = 6 і ексцентриситет e 32 ;

3)вісь 2а = 16 і ексцентриситет e 54 ;

4)рівняння асимптот y ) 43 x і відстань між фокусами 2с = 20;

5)точки М1(6; –1) і М2(–8; 2 2 ) знаходяться на гіперболі;

2.70.Знайти ексцентриситет гіперболи при умові, що 1) кут між асимптотами дорівнює 60о; 2) кут між асимптотами дорівнює 90о.

2.71.Побудувати параболи, що задані рівняннями: 1) у2 = 6х;

122

Розділ II. Аналітична геометрія

2)у2 = –6х;

3)х2 = 6у;

4)х2 = –6у;

атакож їх фокуси та директриси. Написати рівняння директрис.

2.72. Скласти рівняння параболи, вершина якої знаходиться в початку координат. Знаючи, що:

1)парабола розміщена симетрично відносно осі Ох і проходить через точку М(9; 6);

2)парабола розміщена симетрично відносно осі Ох і проходить через точку Р(–1; 3);

3)парабола розміщена симетрично відносно осі Оу і проходить через мочку Q(1; 1);

4)парабола розміщена симетрично відносно осі Оу і проходить через мочку R(4; –8).

2.73.Скласти рівняння параболи і її директриси, якщо парабола проходить через точки перетину прямої х + у = 0 і кола х2 + у2 – 4х = 0

ісиметрична відносно осі Оу.

2.74.Відстань між двома торговими організаціями дорівнює 8 км. Знайти рівняння множини всіх можливих місцезнаходжень баз, які обслуговують ці організації, якщо відомо, що сума відстаней від бази до них повинна бути постійною та дорівнювати 20 км.

2.75. Відстань між двома заводами, що виробляють однакову продукцію, дорівнює 400 км. Транспортні витрати на перевезення продукції від заводу А складають 2 грош. од. за 10 км, а від заводу В — 3 грош. од. за 10 км. Визначити межу районів, для яких однако+ во вигідно придбання продукції та підприємстві А, так і на підпри+ ємстві В.

123