Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Черновицкий национальный университет им. Ю. Федьковича

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Vyscha_matematyka_v_prykladakh_i_zadachakh.pdf

Скачиваний:

Добавлен:

23.02.2016

Размер:

3.55 Mб

Скачать

☆

<<< < Предыдущая 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 3738 / 4038 39 40 > Следующая >>>

Розділ VIII. Ряди

§8.7. Ряди Фур’є

8.7.1. Розклад в ряди Фур’є функції з періодом 2$

Нехай f(x) — функція з періодом 2$ , що інтегрується на [ $;$]. Ряд виду:

a0	(a	cos x b sin x) (a	2	cos 2x b	sin 2x) (a	cos 3x b	sin 3x)

2	1	1		2	3	3

+ (an cos nx bn sin nx) + ...							(8.34)

називається тригонометричним рядом функції f(x). Числа а1, а2, ... , аn, ..., b1, b2, b3, … , bn, … називаються коефіцієнтами тригонометрич, ного ряду. Цей ряд в скороченому вигляді може бути записаний так:

(an cos nx bn sin nx) .

(8.34)

n 1

Тригонометричний ряд називається також рядом Фур’є, коефіці+

єнти якого визначаються за формулами:

а =

f (x)dx ;

а =

f (x)cosnxdx

(n = 1, 2, 3, ...);

(8.35)

bn =

$H f (x)sin nxdx

(n = 1, 2, 3, ...).

При цьому пишуть так:

f(x) #

(an cos nx bn sin nx).

(8.36)

n 1

Ряд Фур’є функції f(x) не завжди своєю сумою має f(x), якщо навіть збігається. Найпростішими достатніми ознаками розкладу функції в ряд Фур’є є:

539

Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»

1. Якщо функція f(x) з періодом 2$ має на відрізку [ $ ;$ ]

скінчене число точок розриву першого роду і абсолютно інтегрована на цьому відрізку, то ця функція розкладається в свій ряд Фур’є в кожній точці, в якій вона диференційовна.

2. Якщо функція з періодом 2$ задовольняє умовам Дірихле на відрізку [ $ ;$ ] (якщо цей відрізок може бути розбитий на скінчене

число частин так, що всередині кожної частини функція монотонна і обмежена), то ця функція розкладається в свій ряд Фур’є в кожній точці неперервності, якщо ж х — точка розриву, ряд Фур’є збігається до числа:

f (x 0) f (x 0) . 2

Ряд Фур’є парної функції, тобто f(x) = f(–x), не містить членів з синусами; цей ряд має вигляд:

					a0	/
				f(x) #	a0	an cos nx ,	(8.37)
				f(x) #	2	an cos nx ,	(8.37)
					2	n 1
		2	$
де	а =		H	f (x)dx ;
де	а =	$		f (x)dx ;
	0

			0
		2	$
	а =	$	H	f (x)cos nxdx , (n = 1, 2, 3, ...).
	а =			f (x)cos nxdx , (n = 1, 2, 3, ...).
	n
			0

Ряд Фур’є непарної функції, тобто f(–x)= –f(x), не містить вільного члена і членів з косинусами; цей ряд має вигляд:

				/
				f(x) # bn sin nx ,	(8.38)
				n 1
		2	$
де	b =		H	f (x)sin nxdx , (n = 1, 2, 3, ...).
де	b =			f (x)sin nxdx , (n = 1, 2, 3, ...).
	n	$
		$
			0

540

Розділ VIII. Ряди

8.7.2. Розв’язання прикладів

Приклад 8.42. Розкласти в ряд Фур’є функцію

																						1				( $ , x , 0)
											f (x)													,
																						2		,
																						2														.
																				1,							(0 , x $ )									.


Розв’язок. Обчислимо коефіцієнти Фур’є функції f(x):
			1		$								1		0						1						$							1			1		0	$
					$										0												$													$
						H f(x)dx
а0	=										=			H									dx H1dx										=			(		х	+ х	) =
а0	=		$								=		$	H									dx H1dx										=	$		(	2	х	+ х	) =
			$		$								$		$						2						0							$			2		$	0
=		1	(				1		$ + $ ) =						1		;
=	$		(						$ + $ ) =						2		;
	$				2										2
			1		$															1					0				1								$
аn	=					H f(x)cosnxdx =																			H						cosnxdx H1cosnxdx =
аn	=		$			H f(x)cosnxdx =														$					H						cosnxdx H1cosnxdx =
			$			$														$					$				2								0
=		1	(				1			sin nx			0		+			1			sin nx							$	) = 0;



	$						2n					$							n									0
			1		$																	1		0						1								$
bn	=					H f (x)sin nxdx =																		H								sin nxdx H1sin nxdx =
bn	=		$			H f (x)sin nxdx =														$				H						2		sin nxdx H1sin nxdx =
			$			$														$				$						2								0
	1				1						0				1												$						3(1 ( 1)n )
	1				1						0				1												$						3(1 ( 1)n )
=			(					cos nx			$ –								cos nx								0 ) =												;
=		$	(	2n				cos nx			$ –					n			cos nx								0 ) =								2$ n				;

так як cos $ n = (–1)n, то

b2k = 0, (k = 1, 2, 3, …),

b2k+1	=	3		, (k = 1, 2, 3, …).
		$(2k	1)

Функція f(x) задовольняє умовам Дирихле, а через це розкла+ дається в свій ряд Фур’є. Отже, в кожній точці неперервності:

541

Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»

	1		3	/	sin(2k 1)x
f(x) =		+					.

4		$		k 0	2k 1
Приклад 8.43. Розкласти в ряд Фур’є функцію f(x) = x (–$
Розв’язок. Задана функція задоволь+								Y
няє умовам Дирихле і через це може

бути розкладена в ряд Фур’є. На інтер+
валі (–$ < x <$ ) функція f(x) = x —
непарна (див. рис. 8.1). Звідси слідує, що
ряд Фур’є цієї функції буде містити						$		0
тільки синуси.

Знайдемо bn.

< x < $ ).

			2	$
bn =			$	H		f (x)sin nxdx					=					Рис. 8.1.
				0
	2		$						u x,			du dx
			$						u x,			du dx
=			H0 x sinnxdx =						dv sin nxdx,			v Hsin nxdx						1	cosnx	=
=	$																	1
	$
																		n
		2			1			$		1	$		2		1		$
								$			$						$
=			(				cos nx	+			Hcosnxdx ) =			(		cos nx		+
=			(				cos nx	+		n	Hcosnxdx ) =			(		cos nx		+
$					n			0		n	0	$			n		0
$					n						0	$			n

2 1

sin nx

0 ) =

(–1)n = (–1)n+1

;

b = (–1)n+1

Отже,

sin nx

x = ( 1)n 1

sin nx = 2 ( 1)n 1

n 1

В розгорнутому вигляді, надаючи n значення 1, 2, 3, ... , одержуємо:

x = 2(	sin x	–	sin 2x	+	sin3x	–	sin 4x	+ …).
1		2		3		4

542

2$ , задовольняє

Розділ VIII. Ряди

Вінтервалі (–$ ;$ ) ця функція має місце в точках непервності

функції f(x), тобто в даному випадку у всіх внутрішніх точках інтер+ валу (–$ ;$ ). Поза інтервалом цей ряд зображає періодичне провод+ ження розглянутої функції.

Вточках же розриву, якими являються точки )$ , )3$ , ..., сума ряду дорівнює середньому арифметичному її лівосторонньої та пра+ восторонньої границі в цих точках.

Знайдемо ці границі. Наприклад, в точці х = $ .

lim f(x) =	lim x = $ ;
x9$ 0	x9$ 0
lim f(x) =	lim x = –$ .
x9$ 0	x9$ 0

Середнє арифметичне цих границь:

f ($ 0) f ($ 0)	$ $	0.
2	2

У всіх точках розриву цієї функції одержуємо те ж саме. Таким чином, в точках розриву сума ряду буде дорівнювати нулю. Отже, одержаний розклад можна записати і так:

2(	sin x		sin 2x		sin3x		sin 4x	x,		якщо $ , x , $
		–		+		–		+ …) =	0,	якщо x (2k 1)$
	1		2		3		4

де k — будь+яке ціле число.

Приклад 8.44. Розкласти в ряд Фур’є функцію f(x) = |x| (–$ < x $ ). Розв’язок. Це неперервна функція з періодом

умовам розкладу в ряд Фур’є, вона парна. Знаходимо:

2				$		2		$			2 x			2		$
2				H f (x)dx		2		Hxdx			2 x						= $ ;
a0 =					=					=
a0 =			$		=		$			=	$	2				0
				0				0								0
an =		2		$H f (x)cos nxdx				=	2	$Hx cosnxdx							=
an =		$		$H f (x)cos nxdx				=	$	$Hx cosnxdx							=
				0						0
=	u x,					du dx												=
	u x,					du dx
	dv cos nxdx,					v Hcos nxdx							1		sin nx
	dv cos nxdx,					v Hcos nxdx							n		sin nx

543

Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»

	2		1		$	2	$					2		1			$
=	2	(x	1	sin nx	–	2	Hsin nxdx ) =					2	(0 +	1	cos nx		) =
=	$	(x		sin nx	–	$	Hsin nxdx ) =						(0 +	2	cos nx		) =
	$		n		0	$	0				$			n			0
					0		0										0
	2							0,			якщо n парне
	2
=			(cos np – 1) =					4								.
=			(cos np – 1) =					4								.
	$ n2									,	якщо n непарне
	$ n2							$ n	2	,	якщо n непарне
								$ n

Отже,
\|x\| =	$	–	4	(cos x+	1	cos 3x+	1	cos 5x +…+	1	cos(2n +1)x + …).
\|x\| =	2	–	$	(cos x+	9	cos 3x+	25	cos 5x +…+	(2n 1)2	cos(2n +1)x + …).

Приклад 8.45. Розкласти в ряд Фур’є функцію f(x)=x, що задана

на інтервалі (0; 2$ ).

Розв’язок. На рис. 8.2 показано графік заданої функції з її періо+ дичним продовженням. Аналітичний вираз функції співпадає з ана+ літичним виразом функції в задачі 8.43. проте між ними маємо істот+

ну відмінність. В задачі 8.43	Y
функція f(x) = x задавалась	Y
на інтервалі (–$ ;$ ), а в цій

	задачі на інтервалі (0; 2$ ). Їх
	відмінність легко бачити із
	графіків функцій. Функція	4$ 2$
	f(x)= x на інтервалі (0; 2$ )	4$ 2$
	f(x)= x на інтервалі (0; 2$ )
	не належить а ні до класу
	парних, а ні до класу непар+
	них.
	Якщо функція f(x) задана не в інтервалі

0 2$ 4$ Х

Рис. 8.2.

(–$ ;$ ), а в інтервалі

(0; 2$ ), також довжиною 2$ , то її можна розкласти в ряд Фур’є того ж виду, що і (8.36), але коефіцієнти визначаються за форму+ лами:

1 2H$

а0 = $ 0 f (x)dx ;

544

Розділ VIII. Ряди

	1	2$
а =	$	H	f (x)cosnxdx ;
а =			f (x)cosnxdx ;
n
		0
	1	2$
b =	$	H	f (x)sin nxdx .
b =			f (x)sin nxdx .
n
		0

В нашому випадку маємо:

		1		2$						1		x2	2$
а =				H		xdx =								= 2$ ;
а =		$				xdx =				$	2			= 2$ ;
0		$								$	2
0
				0									0
						1		2$
		а =				$		H	x cosnxdx = 0;
		а =							x cosnxdx = 0;
			n
								0
					1	2$									2
	bn =				1		H	x sin nxdx =								.
				$

						0									n

Підставляючи одержані значення в формулу (8.36), одержуємо:

x = $	– 2(	sin x	+	sin 2x	+	sin3x	+	sin 4x	+ …).
		1		2		3		4

Так як на інтервалі (0; 2$ ) функція f(x) = x неперервна, то одер+ жаний ряд збігається до х у всіх точках цього інтервалу. В точках х

= 2$ n (n = 0, 1, 2, …), які являються точками розриву функції ряд збігається до середнього арифметичного ліво+ та правосторонніх гра+ ниць функції, тобто до числа

f (2$ 0) f (2$ 0)	2$ 0	= $ .
2	2

Отже, в точках розриву сума ряду дорівнює $ .

545

Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»

8.7.3. Розклад в ряд Фур’є функцій, що задані на півперіоді

Функцію, що задана на півперіоді (0; $ ) можна розкласти (по бажанню) в ряд синусів або в ряд косинусів, продовжуючи на дру+ гий півперіод (–$ ; 0) відповідно непарним або парним чином.

а) Якщо потрібно розкласти таку функцію в ряд по косинусам, то із інтервалу (0; $ ) в сусідній інтервал (–$ ; 0) необхідно зробити парне продовження функції, а потім поза інтервалом (–$ ;$ ) вико+

нати її періодичне продовження з періодом 2$ . Ряд буде мати вигляд

	a0	/
f(x) =		+ an cosnx ,
	2
		n 1

а коефіцієнти визначаються за формулою:

2 $

an = $ H0 f (x)cos nxdx .

б) Якщо ж потрібно функцію f(x), що задано в інтервалі (0; $ ) розкласти в ряд по синусам, то в сусідній інтервал (–$ ; 0) потрібно зробити її непарне продовження, а потім періодично продовжити її з

періодом 2$ .

В цьому випадку ряд буде мати вигляд:

				/
	f(x) = bn sin nx ;
				n 1
а коефіцієнти bn визначаються за формулою:
		2	$
b =			H	f (x)sin nxdx .
		$	H

n
			0
8.7.4. Розв’язання прикладів
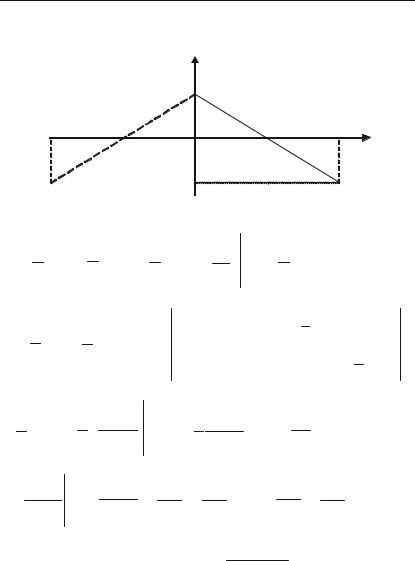
Приклад 8.46. Функцію f(x) =					$	–	x	розкласти в ряд коси+
Приклад 8.46. Функцію f(x) =					4	–		розкласти в ряд коси+
					4	2

нусів на інтервалі (0; $ ).

546

Розділ VIII. Ряди

Розв’язок. Продовжуючи цю функцію парним чином, як показано на рис. 8.3 — пунктиром, будемо мати:

										$
										4
			$			$				0	$				$	X
						2			$		2
									$
										4
										Рис. 8.3.
		2	$H($		x )dx =		2		$	х – x2	$	2	( $ 2		– $ 2
а0 =		2	$H($		x )dx =		2	(	$	х – x2	) =	2	( $ 2		– $ 2	) = 0.
		$ 0		4 2			$		4	2	0	$		4	4
аn =		2	$	$	x				u $4 $2 ,		du 12 dx					1		=
аn =		$	H(	4	2)cos nxdx =				dv cosnxdx, v Hcosnxdx							1	sinnx	=
			0						dv cosnxdx, v Hcosnxdx								sinnx
			0
																n
= 2		((	$	–	x ) sin nx		$	– $H 1 sin nx dx ) =					1	$Hsinnxdx =
$			4		2	n	0		0	2 n			$ n 0
	cosnx $					cos$ n		1		1		1			1
= –		$ n2		0	= –	$ n2	+ $ n2			= $ n2	– (–1)n	$ n2		=	$ n2 (1 – (– 1)n);
				0
											2
						a2k = 0;				a2k+1 = $(2k 1)2 .

Отже,

547

Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»

												$							x						2		/		cos(2k 1)x
																	–					=																				.
												4					–	2				=		$								(2k						1)		2		.
												4						2						$			k 0					(2k						1)
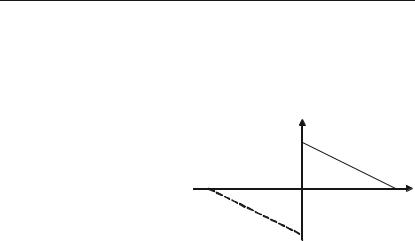
Приклад 8.47. Функцію f(x) =																															1		$		–				1		x розкласти в ряд си+
нусів на інтервалі (0; $ ).																													2									2
нусів на інтервалі (0; $ ).																																									Y
Розв’язок. Продовжуючи																																										$
цю функцію непарним чином,																																										4
як показано на рис. 8.4. пунк+
тиром, будемо мати:																											$															0				$ X
																											$															0				$ X
	2			$							x																															$
bn =	2				H($						x		)sin nxdx =																														4
bn =	$				H($								)sin nxdx =																														4
	$			0		2		2																																	Рис. 8.4.
		u				$				x		,					du								1	dx
										x															1
																									2
						2		2																	2
=		dv sin nxdx,															v Hsin nxdx																			cosnx						=

																																							n
	2					$								x cos nx													$		1								cos nx
																							$

=			(–( 2					–								)									– H0									(									)dx) =
=	$		(–( 2					–						2		)	n						0		– H0							2		(					n				)dx) =

	1						sin nx								$			1
=	1				–		sin nx										=	1		.

	n						$ n2								0			n
Отже,
					1			1													sin 2x									sin3x												/		sin nx
					1	–		1	x = sin x +												sin 2x							+		sin3x								+ … =						sin nx		.
				2		–		2	x = sin x +																			+										+ … =								.
				2				2														2							3														n 1		n

548

Розділ VIII. Ряди

8.7.5. Розклад в ряд Фур’є функції з періодом 2l

Якщо період функції f(x) дорівнює не 2$ , а 2l, то її ряд Фур’є має вигляд:

	a0	/	$ nx	/	$ nx
f(x) =		+ an cos		+ bn sin		,	(8.39)
	2		l		l
		n 1		n 1

а коефіцієнти цього ряду а0, аn, bn обчислюються за формулами:

$ nx

а =

f (x)cos

dx , (n = 0, 1, 2, 3, …);

$ nx

b =

f (x)sin

dx .

(8.40)

Якщо функція f(x) на інтервалі (–l; l) парна, то всі коефіцієнти bn = 0, її розклад в ряд Фур’є містить тільки сталу і косинуси і має

вигляд:

f(x) = a0

/$ nx

+an cos l .n 1

Коефіцієнти розкладу аn дорівнюють в цьому випадку:

	2	l		$ nx
а =	l	H	f (x)cos	l	dx , (n = 0, 1, 2, 3, …).
а =			f (x)cos		dx , (n = 0, 1, 2, 3, …).
n
		l

Якщо ж на інтервалі (–l; l) функція f(x) — непарна, то а0 = аn = 0, її ряд Фур’є містить тільки синуси та має вигляд:

				/		$ nx
	f(x) = bn sin					$ nx		,
				n 1		l
а коефіцієнти
		2	l		$ nx
b =		l	H	f (x)sin		l	dx .
b =				f (x)sin			dx .
n

549

Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»

8.7.6. Розв’язання прикладів

Приклад 8.48. Розкласти в ряд Фур’є функцію

6,	якщо 0 , x , 2,
f (x)	якщо 2 , x , 4.
3x,	якщо 2 , x , 4.

Розв’язок. Користуючись формулами (8.40), маючи l = 2 та роз+ биваючи інтервал інтегрування (0; 4) точкою х = 2 на дві частини, так як в кожній із них функцію задано різними формулами, одер+ жуємо:

an =					1			H4			f (x)cos			$ nxdx					=		1		( H2		6cos		$ nxdx							+		H4		3x cos $ nxdx ) =
an =				2				H4			f (x)cos			$ nxdx					=	2			( H2		6cos		$ nxdx							+		H4		3x cos $ nxdx ) =
				2				0						2						2				0					2							2							2
								0																0												2
=		1		(			12				sin		$ nx			+ 3(			2x			sin		$ nx +						4				cos			$ nx )					4 ) =
=		1		(			12				sin		$ nx		2	+ 3(			2x			sin		$ nx +						4				cos			$ nx )					4 ) =
	2						$ n						2		0				$ n							2			$ 2n2									2				2
															0																											2
=	6								(1– cos pn),								n 0.
=		$ 2n2							(1– cos pn),								n 0.
		$ 2n2
	Якщо n парне: cos pn = 1 і an = 0;
	Якщо n непарне: cos pn = –1 і an =																												12			;

																												$ 2n2
	Якщо n = 0 за формулою (8.40) одержуємо:
						1		4									1	( 2						4							1									3x2
																																					2							4
																																					2							4
a =											f (x)dx			=					6dx +							3xdx ) =								(6x				+						) = 15.
0				2					H							2		H						H							2						0				2			2
0
								0										0						2
								4																2												4
bn =						1			H f (x)sin						$ nxdx				=			1	( H6sin				$ nxdx							+		H3x sin $ nxdx ) =
bn =				2					H f (x)sin						$ nxdx				=	2			( H6sin				$ nxdx							+		H3x sin $ nxdx ) =
				2				0						2						2				0					2							2							2
			1		(					12		cos $ nx					2			4						sin $ nx							2x		cos $ nx )								4


=																		+ 3(												–													) =
	2									$ n			2				0			$ 2n2							2						$ n						2				2

550

Розділ VIII. Ряди

= 2$1n (12(1 – cos np) + 3(4cos np – 8)) = n6$ . Шуканий розклад заданої функції має вигляд:

f(x) =			15		+	12		(cos			$ x		+		1	cos			3$ x			+		1	cos	5$ x	+ …) –
f(x) =					+			(cos					+	9		cos						+			cos		+ …) –
				2		$ 2					2			9						2			25			2
–	6	(sin $ x					+		1	sin		2$ x		+			1	sin			3$ x		+ …).
	$				2			2			2					3				2

Цей розклад справедливий на всій області визначення даної функції: в інтервалі (0; 2) сума ряду S(x) = 6, а в інтервалі (2; 4) S(x) = 3х. В точці розриву х = 2, де функція не визначена

S(2) =	1	( lim f(x) +	lim f(x)) = 6.
	2
		x92 0	x92 0

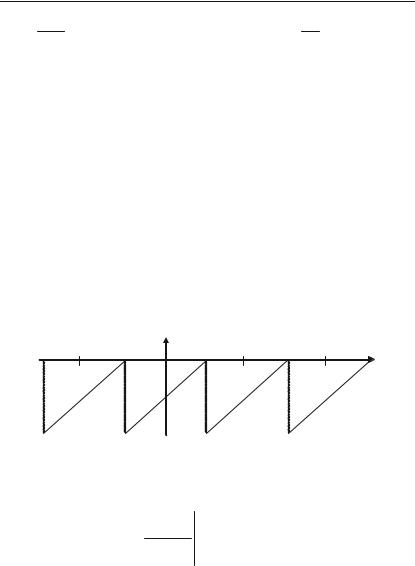
Приклад 8.49. Розкласти функцію в ряд Фур’є f(x)

інтервалі –1< x 1.

Розв’язок. Графік функції зображено на рис. 8.5.

= x – 1 на

–3	–2	–1	0			1	2	3	4	5
			–1
			–2
			Рис. 8.5.
Знаходимо коефіцієнти Фур’є, знаючи, що l = 1.
a0 = H1	(x 1)dx =		(x 1)2 1			= –2;
1			2	1
1				1
an = H1	(x 1)cos n$ xdx = H1				x cosn$ xdx – H1				cosn$ xdx =
1				1				1

551

Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»

x sin$ nx

1 sin n$ x

sin$ nx

–

dx –

cos npx

$ n

n $

bn = H1

(x 1)sin n$ xdx = H1

x sin n$ xdx – H1

sin n$ xdx =

x cos$ nx

+ H1

cos n$ x

dx +

cos$ nx

$ n

(cos n$

+ cos( n$ )) +

sin n$ x

(cos n$

n2$ 2

– cos( n$ )) = 2( 1)n . n$

Зокрема,

b =		2	, b =	2	,	b =	2	, …
	$			2$			3$
1			2			3

= 0;

–

Ряд Фур’є для функції f(x) має вигляд:

2			sin x		sin2x		sin3x		sin nx
x – 1 = –1 +		(		–		+		– ... + (–1)n+1		+ …).
x – 1 = –1 +	$	(	1	–	2	+	3	– ... + (–1)n+1	n	+ …).

8.7.7. Приклади для самостійного розв’язку

Приклад 8.50. Розкласти в ряд Фур’є функцію f(x) = х2 для зна+ чень х на відрізку [ $ ;$ ] .

$ x

Приклад 8.51. Розкласти в ряд Фур’є функцію f(x) = 2	в
інтервалі ( $ ;$ ) .

552

Розділ VIII. Ряди

Приклад 8.52. Розкласти в ряд Фур’є функцію

2,	якщо	$ , x , 0,
f (x)	якщо	0 х , $.
1,	якщо	0 х , $.
Приклад 8.53. Розкласти в ряд Фур’є функцію f(x) =			x	в інтер+

			2

валі (0; 2$ ).

Приклад 8.54. Розкласти в ряд Фур’є функцію f(x) = 2х – 3 в інтервалі (–3; 3).

Приклад 8.55. Розкласти в ряд Фур’є функцію

1,		якщо	3 , x , 0,
f (x)	2,	якщо	0 х , 3.

Приклад 8.56. Розкласти в ряд Фур’є функцію f(x) =|х| – 1 в інтервалі (–2; 2).

Приклад 8.57. Розкласти в ряд Фур’є функцію

0,		якщо	2 x 0,
f (x)	x,	якщо	0 х 2.

553

<<< < Предыдущая 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 3738 / 4038 39 40 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.09.2019166.74 Кб2vse_razom.docx
#
18.12.2018166.05 Кб2vsi_gotovi_shpori.docx
#
03.09.2019249.86 Кб2VSTUP-1.doc
#
01.05.2019130.05 Кб21Vstup_do_psikhosomatiki.doc
#
25.11.2018205.31 Кб1Vstup_do_spec 2008.doc
#
23.02.20163.55 Mб63Vyscha_matematyka_v_prykladakh_i_zadachakh.pdf
#
20.11.2018475.14 Кб14vystavky.doc
#
23.02.2016178.81 Кб22Yatsenyuk_Petro_6 ШПОРИ.docx
#
23.02.2016783.36 Кб117Yuridichna_psikhologiya_Vidpovidi.doc
#
23.02.20161.42 Mб47Zadachni_copy.pdf
#
23.02.2016420.92 Кб141Zagalna_Psihologia-Variy.pdf