
- •Vііі. Загальні вказівки про порядок виконання лабораторних робіт
- •§1. Підготовка та виконання
- •§2. Вимоги до звіту і захисту
- •§3. Основні правила техніки безпеки під час роботи в лабораторії
- •Основні правила техніки безпеки при роботі з приладами, які живляться від електричної мережі
- •Після закінчення роботи
- •Похибки фізичних вимірювань та математична обробка результатів експериментальних досліджень.
- •§ 1. Фізичні вимірювання та їх класифікація.
- •§ 2. Похибки фізичних вимірювань та їх класифікація.
- •§ 3.Визначення похибок прямих вимірювань фізичних величин.
- •§ 4. Оцінка похибок непрямих вимірювань.
- •§ 5.Математична обробка результатів фізичних вимірювань.
- •§ 6. Порядок виконання математичної обробки експериментальних результатів.
- •Лабораторна робота № 1 Прямі і непрямі виміри та визначення їх похибок
- •I. Прості фізичні виміри
- •Виміри штангенциркулем.
- •II. Прямі виміри, математична обробка результатів. Вимірювання і визначення похибки прямих вимірювань
- •III. Визначення густини тіла правильної геометричної форми.
- •Лабораторна робота № 2 визначення прискорення вільного падіння за допомогою машини атвуда
- •Лабораторна робота № 3 визначення швидкості кулі за допомогою балістичного крутильного маятника
- •Лабораторна робота № 4 визначення пружного і непружного ударів двох куль
- •Лабораторна робота № 5 визначення моменту інерції маятника максвелла
- •Лабораторна робота № 6 визначення моменту інерції тіла за допомогою маятника обербека.
- •Лабораторна робота № 7 визначення моменту інерції і моменту імпульсу гіроскопа
- •Лабораторна робота № 8 визначення коефіцієнта тертя кочення за допомогою похилого маятника
- •Лабораторна робота № 9 визначення густини твердих тіл і рідин
- •І. Визначення густини твердих тіл методом гідростатичного зважування
- •Іі. Визначення густини рідини за допомогою пікнометра
- •Лабораторна робота № 10 визначення коефіцієнту в’язкості рідини методом стокса
- •Лабораторна робота № 11 Визначення модуля Юнга тонкої дротини
- •Лабораторна робота № 12 Визначення моменту інерції та модуля зсуву тонкої дротини
- •Лабораторна робота № 13 Визначення прискорення вільного падіння за допомогою математичного і оборотного маятників
- •Лабораторна робота № 14 Визначення швидкості звуку в повітрі методом резонансу
- •Лабораторна робота № 15 Визначення швидкості звуку в стержні методом Кундта
- •Лабораторна робота № 16 Експериментальна перевірка рівняння Бернуллі
§ 4. Оцінка похибок непрямих вимірювань.
§ 4-1. Метод частинного диференціювання.
При непрямих вимірах шукану величину визначають за результатами прямих вимірів інших величин, функцією яких вона є. Тому похибки при вимірюванні цієї величини визначаються за похибками безпосередньо вимірюваних величин.
Нехай, шукана фізична величина є функцією N величин, що вимірюються безпосередньо:
![]()
Найбільш ймовірне значення функції Y, тобто середній результат непрямого вимірювання, одержується при підстановці середньо–арифметичних значень аргументів:
![]() ,
де k=1,
… n
,
де k=1,
… n
і кожна із величин <xn> знайдена з певною похибкою. Для обчислення абсолютної похибки непрямих вимірювань застосовують метод частинного диференціювання функції декількох змінних, тобто знаходять повний диференціал функції Y:
![]()
де
![]() - модулі частинних похідних функційY,
знайдені для середніх значень аргументів
- модулі частинних похідних функційY,
знайдені для середніх значень аргументів
![]() .
.![]()
Так як
dY![]()
![]() Y
, dx
Y
, dx![]()
![]()
![]() , dx
, dx![]()
![]()
![]() ,
dx
,
dx![]()
![]()
![]() …
dx
…
dx![]()
![]()
![]() …
…
то
![]()
Переходячи до квадратичного додавання, отримуємо формулу для підрахунку середньої абсолютної похибки остаточного результату:

Відносна похибка непрямих вимірювань обчислюється за формулою:
![]()

Остаточний результат непрямого вимірювання записується у вигляді:
![]() од.
вимірювання при р=0,95
і Е , %.
од.
вимірювання при р=0,95
і Е , %.
Приклад: нехай робоча формула для знаходження питомої теплоти пароутворення води має вигляд:
![]()
Так як
вираз, за допомогою якого визначається
значення питомої теплоти пароутворення,
не логарифмується, то спочатку доцільно
знайти абсолютну похибку, застосовуючи
метод частинного диференціювання. Для
цього визначимо частинні похідні від
![]() по кожній з вимірюваних величин, вважаючи
їх змінними:
по кожній з вимірюваних величин, вважаючи
їх змінними:
![]() ;
;
![]() ;
;![]() ;
;
![]() ;
;
![]()
Знайдемо повний диференціал шуканої величини:
![]()
Взявши
суму абсолютних значень частинних
похідних і зробивши заміну знаку d
на знак
![]() та переходячи до квадратичного додавання,
одержимо формулу для обчислення
абсолютної похибки:
та переходячи до квадратичного додавання,
одержимо формулу для обчислення
абсолютної похибки:
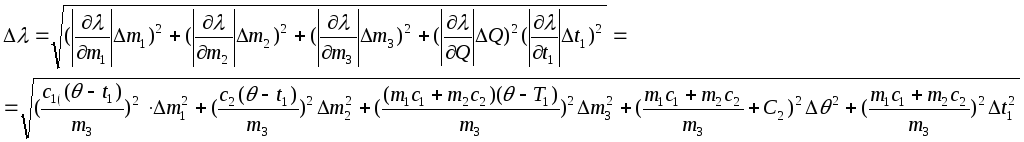
Відносна похибка підраховується за формулою:
![]() при
р=0,95
при
р=0,95
Кінцевий
результат:
![]() прир=0,96
і
Е, %
прир=0,96
і
Е, %
§ 4-2. Метод логарифмічного диференціювання.
Якщо розрахункова формула для визначення остаточного результату непрямих вимірювань є вираз, зручний для логарифмування, то в цьому випадку доцільно застосувати метод логарифмічного диференціювання (метод диференціювання натурального логарифма).
Нехай, розрахункова формула має вигляд:
![]()
де
![]() - будь – які раціональні числа. Тоді,
проводячи логарифмування попереднього
виразу, маємо:
- будь – які раціональні числа. Тоді,
проводячи логарифмування попереднього
виразу, маємо:
![]()
Після визначення повного диференціалу натурального логарифму одержимо:
![]()
Замінюючи диференціали вимірюваних величин відповідними абсолютними похибками цих величин, одержаними при їх вимірюваннях, і взявши їх за модулем, дістанемо вираз для розрахунку максимальної відносної похибки:
![]()
Більш точніший вираз отримаємо, переходячи до квадратичного додавання:

де
![]() - відносні похибки окремих прямих
вимірювань.
- відносні похибки окремих прямих
вимірювань.
Приклад. Нехай розрахункова формула для обчислення густини твердого тіла циліндричної форми має вигляд:

Проведемо логарифмування виразу:
![]()
Визначимо повний диференціал натурального логарифму:
![]()
Замінюючи диференціал вимірюваних величин відповідними абсолютними похибками, знак “-” на знак “+”, одержимо формулу для абсолютного підрахунку максимальної відносної похибки:
![]()
Квадратичне додавання приводить до виразу:
![]()
Максимальна абсолютна похибка визначається за формулою:
![]()
Кінцевий результат подаємо у вигляді:
![]()
при р=0,95 і ε , %
Примітка: якщо шукана величина Y дорівнює сумі або різниці вимірюваних величин, то спочатку доцільно знайти абсолютну похибку, а потім – відносну.
Нехай,
![]() ,
,
тоді
![]()
![]()
Квадратичне додавання дає формулу:
![]()
![]()
