4.6. Вырожденные злп, алгоритм их решения

Опорное решение называется вырожденным, если хотя бы одна базисная переменная равна нулю.

Это означает, что при решении вырожденной задачи может произойти «зацикливание», так как нарушается принцип конечности симплекс- метода, т.е. возможна такая ситуация, когда сколько бы итераций не выполняли, никакого определенного вывода получить не удается.

Вырожденное решение может получиться, когда на каком-то шаге при выборе разрешающего элемента получено два или более равных наименьших симплексных отношений . В этом случае возникает вопрос о выборе разрешающей строки.

Разрешающей выбираем строку, в которой будет наименьшее отношение элементов следующего за столбцом свободных членов неединичного столбца к элементам разрешающего столбца. Если же снова получаются равные наименьшие отношения, то составляем отношение элементов следующего неединичного столбца к элементам разрешающего столбца и так далее, пока выбор не будет однозначным.

В дальнейшем алгоритм симплексного метода решения вырожденной задачи остается таким же, как и в случае невырожденной задачи.

Пример 13

Найти минимум функции при ограничениях:

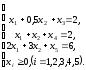
Решение

Система ограничений приведена к единичному базису, базисные переменные , свободные переменные. Свободные члены положительны. Приведенное выражение имеет вид:, исходное опорное решение.

Составим исходную симплексную таблицу.

Базис	x1	x2	x3	x4	x5	ai0	ai0/aip
x3	1	0,5	1	0	0	2	2	0,5
x4	1	1	0	1	0	2	2	1
x5	2	3	0	0	1	6	3	1,5
f	3	1	0	0	0	0

В исходной таблице оценки свободных переменных положительны и в каждом столбце с положительными оценками есть положительные элементы, следовательно, решение можно улучшить. Первый столбец выбираем разрешающим, в силу того, что оценка больше. Но первая и вторая строки имеют одинаковые минимальные симплексные отношения, равные 2. Следовательно, чтобы однозначно выбрать разрешающую строку, составим отношения элементов другого неединичного столбца, следующего за столбцом свободных членов (в таблице второй столбец). Получим отношения: 0,5/1=0,5; 1/1=1; 3/2=1,5. Эти отношения припишем справа к симплекс-таблице. Наименьшим из них есть число 0,5. Таким образом, разрешающая строка - первая, разрешающий элемент. Проведя итерацию, получим новую таблицу:

Базис	x1	x2	x3	x4	x5	ai0	ai0/aip
x1	1	0,5	1	0	0	2
x4	0	-0,5	-1	1	0	0
x5	0	2	-2	0	1	2
f	0	-0,5	-3	0	0	-6

В полученной таблице все оценки отрицательные, следовательно, решение оптимально : .

5. Двойственные задачи

Рассмотрим некоторые элементы теории двойственности, основные идеи которой содержатся уже в ранних работах Л.В. Канторовича.

В экономической теории наиболее часто используют одну из возможных интерпретаций двойственных задач: задачу об использовании сырья и двойственную ей задачу о ценах на ресурсы.