2.3 Формы записи задач линейного программирования: общая, каноническая и стандартная

Система ограничениями (2.2) задачи линейного программирования может содержать как неравенства, так и уравнения. Различают следующие формы записи ЗЛП:

1. Общая форма ЗЛП

- это задача максимиза­ции или минимизации линейной функции с линейными ограничениями в виде как равенств, так и неравенств:

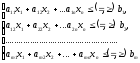
2. Каноническая форма ЗЛП

- это задача максимиза­ции линейной функции с линейными ограничениями в виде ра­венств:

3. Стандартная форма записи ЗЛП

– это задача максимизации (минимизации), если все ограничения – неравенства

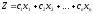
Запишем задачу линейного программирования (стандартная и кононическая формы) в матричном виде:

Найти X(), при котором

_{если выполняются условия}

где:

Замечания

Указанные формы ЗЛП эквивалентны в том смысле, что каждая из них может быть приведена к любой другой путем несложных тождественных преобразований.

Для того чтобы переходить от одной формы записи к другой, нужно уметь преобразовывать задачу минимизации в задачу максимизации и ограничения-равенства к ограничениям-неравенствам (и обратно), а также уметь изменять знаки неравенств на противопо­ложные.

• Задача минимизации (максимизации) функции Z эквива­лентна задаче максимизации (минимизации) функции (-Z),

так как

• Уравнение АX=В эквивалентно двум неравенствам: .

• Переход от неравенств к равенствам может быть легко осу­ществлен путем добавления в неравенства дополнительных пере­менных, которые затем включаются в оптимизируемую функцию с нулевыми коэффициентами.

Например, от неравенства

перейдем к уравнению, добавив новую балансовую переменную х_n+1

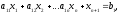
где х_n+10.

Таким образом, все операции, необходимые для перехода от одной формы задачи ЛП к любой другой, известны и легко осущест­вимы.

3. Графический метод решения задачи линейного программирования

При решении ЗЛП графическим методом необходимо, чтобы задача была записана в стандартной форме и переменных в задаче было две .

Запишем математическую модель ЗЛП.

Найти решение такое, чтобы функция

(3.1)

достигала экстремума и выполнялись условия:

, или

, (3.2)

а также ,

или ,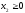(3.3)

Алгоритм решения ЗЛП графическим методом:

1. Построить область допустимых решений ОДР,

удовлетворяющую ограничениям (3.2) и (3.3);

2. Построить вектор – градиент целевой функции

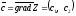
3. Построить линию уровня – прямую, перпендикулярную вектору-градиенту ( );

4. Найти:

«точку входа» - minz – первая точка пересечения линии уровня с ОДР,

«точку выхода» - maxz – последняя точка пересечения линии уровня с ОДР.

Пример 3

Решить графически следующую ЗЛП:

найт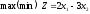и , если

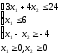
Решение

Построим область допустимых решений (ОДР), для этого необходимо построить границы области – прямые:

324,,

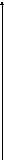
6

А

l4линия уровня

-4 _{c 1.}

В

2

_{-3 x= 6}

Рис.1

Далее строим:

• вектор-градиент ;

• линии уровня 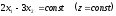, на чертеже эти прямые изображены пунктиром, через начало координат проходит линия уровня, уравнение которой;

Перемещаем линию уровня (прямая l на рис.1) по ОДР (заштрихованная область) в направлении вектора 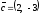, находим точку «входа» в область - точку А , в которой достигается наименьшее значение целевой функции.

Точка А лежит на пересечении прямых 324 ;, чтобы определить ее координаты решим систему уравнений:

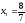; ;Итак, координаты точки А найдены: А(,).

Подставляя найденные значения в целевую функцию, получим:

=.

Перемещая далее линию уровня в направлении вектора , определим точку «выхода» - точкуВ (6; 0).

Наибольшее значение функция принимает в точке В (6; 0) и _.

В предыдущем примере (примере 3) ЗЛП имела единственное оптимальное решение, на практике встречаются и задачи, которые либо не имеют оптимального решения (примере 4) , либо имеют бесконечное множество оптимальных решений (примере 5).

Пример 4

Найти наибольшее и наименьшее значения функции Z = 2х₁+2х₂

при ограничениях х₁-3х₂3

-3х₁+х₂ 3

х₁0, х₂0

Решение

Рис. 2

По условию задачи построим ОДР – множество точек области, координаты которых удовлетворяют условиям ограничений (заштрихованная область).

Перемещая линию уровня (прямая l на рис.2) в направлении вектора-градиента (2,2), найдем «точку входа» О (0,0), таким образом,

Z_min = Z(0) = 0;

«Точку выхода» найти невозможно, так как линия уровня всегда будет пересекать ОДР.

Итак, оптимального решения, при котором целевая функция достигает максимума, не существует, Z_max

Пример 5 (альтернативный оптимум)

Найти наибольшее значение функции Z = 2х₁+2х₂

при ограничениях х₁+х₂

х₁-2х₂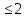

х₁х₂

Решение

Построим ОДР

Рис. 3

Очевидно, что вектор-градиент (2,2) ортогонален границе области – отрезку АВ. Линия уровняl параллельна стороне (рис.3).

Таким образом «точки выхода» - это любые точки отрезка АВ.

Точка имеет координаты А( 0,4);

координаты точки В найдем из системы:

х₁+х₂=4

х₁-2х₂=2

3х₂ = 2; х₂ =; х₁ = 4 -=, итак, В (.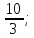

Значение целевой функции будет одно и то же в любой точке отрезка АВ, оно равно

Z(А) = Z(В) = 2·0 + 2·4 = 8.

Данная ЗЛП имеет бесконечно много оптимальных решений

х₁ = t

х₂ = 4-t

где 0 , причемZ_max = 8.

Пример 6

Найти Z = х₁ – 2х₂max

при ограничениях х₁ + х₂

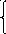2х₁ + 2х₂

х₁

х₂ 0

Решение

В данной ЗЛП область допустимых решений представляет собой пустое множество; очевидно, что в этом случае оптимального решения не существует.

Рис. 4