4.5. Альтернативный оптимум, алгоритм нахождения всех оптимальных решений

Рассмотрим случай, когда задача имеет несколько оптимальных решений

,

вообще говоря, бесчисленное множество решений, которые можно объединить формулой:

,

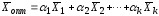где - общее решение ,.

Задача линейного программирования имеет альтернативный оптимум, если в симплексной таблице при решении ЗЛП на максимум окажется хотя бы одна нулевая оценка свободной переменной, при условии, что все остальные положительные.

Алгоритм нахождения всех оптимальных опорных решений

1. Выписать полученное оптимальное решение .

2. Ввести в базис одну из свободных переменных с нулевой оценкой и провести итерацию симплексным методом. Получим новое опорное решение .

3. Итерации повторять до тех пор, пока после введения в базис любой свободной переменной с нулевой оценкой не будет получено уже ранее встречавшееся оптимальное решение. В результате получим все оптимальные решения: .

4. Общее решение ЗЛП записать в виде:

Пример12

Найти максимум функции при ограничениях:

Решение

Исходная система ограничений уже приведена к единичному базису, найдем приведенное выражение для целевой функции выразив базисные переменныечерез свободные

тогда

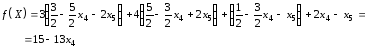Следовательно, приведенное выражение будет: .

Составим исходную симплексную таблицу

Базис	х1	х2	х3	х4	х5	bi0	bi0/bip
x2	0	1	0	3/2	-2	5/2
x1	1	0	0	5/2	2	3/2	3/4
x3	0	0	1	3/2	1	1/2	1/2
f	0	0	0	13	0	15

Так как среди оценок нет отрицательных, то полученное решение будет оптимальным. Ему соответствует максимальное значение целевой функции.

Полученный оптимальный план не является единственным, так как свободной переменной соответствует нулевая оценка. Таким образом, задача имеет альтернативный оптимум.

Найдем другие оптимальные решения:

1. Выпишем оптимальное решение ,.

2. Введем в базис свободную переменную и выведем. Получим следующую таблицу

Базис	х1	х2	х3	х4	х5	bi0	bi0/bip
x2	0	1	2	9/2	0	7/2	7/4
x1	1	0	-2	-1/2	0	1/2
x5	0	0	1	3/2	1	1/2	1/2
f	0	0	0	13	0	15

В последней строке все оценки неотрицательны, тогда решение будет оптимальным,

значение целевой функции .

3. Проведем еще одну итерацию симплексного метода, для чего введем в базис свободную переменную 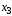, так как эта переменная имеет нулевую оценку. Составим новую таблицу

Базис	х1	х2	х3	х4	х5	bi0	bi0/bip
x2	0	1	0	3/2	-2	5/2
x1	1	0	0	5/2	2	3/2
x3	0	0	1	3/2	1	1/2
f	0	0	0	13	0	15

- это решение было получено ранее, как решение .

Так как свободных переменных с нулевой оценкой нет, которые нужно ввести в базис, значит , на этом процесс решения задачи заканчивается.

4. Запишем общее решение исходной задачи :

.

Положим или, где.

Имеем :

Придавая параметру любые числовые значения от 0 до 1, будем получать различные оптимальные решения задачи, для каждого из которых.