4.3. Критерий оптимальности

Критерий оптимальности полученного опорного решения:

если в последней строке симплексной таблицы – строке целевой функции f - все оценки неотрицательны

_p0,

то полученное опорное решение оптимально.

Оптимальное решение не существует, если в симплексной таблице есть хотя бы одна отрицательная оценка, столбец которой не содержит положительных элементов, в этом случае целевая функция f не ограничена в области допустимых решений:

Пример 9

Проверить критерий оптимальности по заданной симплекс – таблице:

Базис	х1	х2	х3	х4	х5	bi0	bi0 / bip
x1	1	0	4/5	-1/5	0	140
x2	0	1	-3/5	2/5	0	120
x5	0	0	1	-1	1	100
f	0	0	-2	3	0	13200

Решение

Найденное в предыдущем примере 8 опорное решение

Х=(140, 120, 0, 0, 100)

не будет оптимальным, так как в строке целевой функции есть отрицательная оценка ₃= -2 0.

4.4. Невырожденные злп, алгоритм их решения

Опорное решение ЗЛП называется невырожденным, если все базисные переменные строго больше нуля.

Задача называется невырожденной, если все ее опорные решения невырожденные.

Алгоритм решения невырожденной ЗЛП

1. Приводим систему ограничений к единичному базису ( с помощью метода Жордана- Гаусса )

2. Находим приведенное выражение для целевой функции f и заполняем исходную симплексную таблицу.

3. Если все оценки строке целевой функции _p0, то делаем вывод, что полученное решение оптимально и процесс решения задачи окончен.

4. Если есть отрицательная оценка _p<0 и все элементы столбца над этой оценкой отрицательны или равны нулю, то это означает, что f неограниченна, max f и задача решения не имеет.

5. Если есть отрицательная оценка _p<0 и хотя бы один из элементов столбца над ней положительный b_ip>0, то переходим к лучшему опорному решению следующим образом:

• выбираем ведущий p- столбец из условия: наибольшая по модулю оценка _p<0 и хотя бы один из элементов b_ip>0;

• выбираем ведущую q- строку по наименьшему симплексному отношению .

• в симплексной таблице выбираем ведущий элемент b_qp (элемент, стоящий на пересечении q- ой строки и p- того столбца) и выполняем итерацию метода Жордана- Гаусса. Таким образом переходим к новому базису с базисной переменной x_p.

• находим новое опорное решение и проверяем выполнения

критерия оптимальности.

Пример 10

Найти оптимальное решение по заданной симплекс – таблице:

Базис	х1	х2	х3	х4	х5	bi0	bi0 / bip
x1	1	0	4/5	-1/5	0	140
x2	0	1	-3/5	2/5	0	120
x5	0	0	1	-1	1	100
f	0	0	-2	3	0	13200

Решение

Найденное в предыдущем примере 8 опорное решение

Х₁=(140, 120, 0, 0, 100)

не будет оптимальным, так как в строке целевой функции есть отрицательная оценка ₃= -2 0.

Перейдем от исходного опорного решения Х₁ к лучшему Х_2.

В качестве ведущего столбца выберем третий столбец по отрицательной оценке ₃=-2.

Для положительных элементов третьего столбца составим симплексные отношения и запишем их в последнем столбце симплексной таблицы.

В качестве ведущей строки возьмем строку с минимальным симплексным отношением- это третья строка, так как

Базис	х1	х2	х3	х4	х5	bi0	bi0 / bip
x1	1	0	4/5	-1/5	0	140	140:4/5=175
x2	0	1	-3/5	2/5	0	120	-
x5	0	0	1	-1	1	100	100:1=100
f	0	0	-2	3	0	13200

==100,

таким образом, ведущий элемент b₃₃=1.

С этим ведущим элементом проведем одну итерацию метода Жордана- Гаусса, а именно.:

• все элементы ведущей строки разделим на ведущий элемент

(на 1);

• в ведущем столбце все элементы кроме ведущего заменим нулями (запишем единичный столбец);

• все остальные элементы симплекс-таблицы преобразуем по правилу « определителя второго порядка », получим

новую симплекс – таблицу:

Базис	х1	х2	х3	х4	х5	bi0	bi0 / bip
x1	1	0	0	3/5	-4/5	220
x2	0	1	0	-1/5	3/5	180
x5	0	0	1	-1	1	100
f	0	0	0	1	2	13400

Новое опорное решение

Х₂=(220, 180, 100, 0, 0)

будет оптимальным, так как в строке целевой функции все оценки положительные _p0, причем значение целевой функции f_max= f(X₂)=13400.

В следующей задаче составим математическую модель и найдем оптимальное решение симплексным методом.

Пример 11

Составить оптимальный план производства изделий двух видов А и В, обеспечивающий максимальную стоимость их реализации, если на

изготовление единицы изделия А требуется затратить а₁=2 кг сырья первого типа, а₂=3 кг сырья второго типа и а₃=1 кг сырья третьего типа. Для единицы изделия В требуется b₁=1 кг сырья первого типа, b₂=4 кг сырья второго типа и b₃=3 кг сырья третьего типа. Производство обеспечено сырьем каждого типа в количестве 400 кг, 900 кг, 600 кг соответственно. Стоимость единицы изделия А составляет 60 руб., а единицы изделия В- 40 руб.

Решение

Построим математическую модель данной ЗЛП:

Пусть х₁- количество изделий вида А,

х₂- количество изделий вида В.

Тогда потребуется затратить сырья первого типа в количестве

кг на изделия вида А и b₁х₂ кг на изделия вида В. Значит, общие затраты сырья первого типа по плану составят кг. Аналогично, сырья второго типа в килограммах потребуется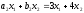и сырья третьего типа а₃х₁+b₃х₂=х₁+3х₂. При реализации всех изделий будет получено 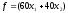рублей.

Нужно найти такие планы производства х₁, х₂, чтобы выполнялись условия данной задачи по запасам сырья трех типов:

и при этом функция f=60х₁+40х₂

должна достигать максимума.

Решим задачу симплексным методом

Запишем эту задачу в канонической форме, введя дополнительные балансовые переменные х₃, х₄, х₅, которые имеют смысл остатков сырья соответственно первого, второго и третьего типов.

Тогда система ограничений имеет вид:

и приведенное выражение для целевой функции f

Очевидно, что система ограничений приведена к единичному базису:

базисные переменные- х₃, х₄, х₅,

свободные переменные- х₁, х₂.

Составим исходную симплекс- таблицу.

Базис	х1	х2	х3	х4	х5	bi0	bi0 / bip
x3	2	1	1	0	0	400	400:2=200
x4	3	4	0	1	0	900	900:3=300
x5	1	3	0	0	1	600	600:1=600
f	-60	-40	0	0	0	0

исходное опорное решение получим при х₁=х₂=0 равное

Х₀=(0, 0, 400, 900, 600)

В строке целевой функции обе оценки свободных переменных(-60;-40) отрицательны. Следовательно, решение Х₀=(0, 0, 400, 900, 600) не является оптимальным.

В каждом столбце с отрицательной оценкой все элемент- положительные, следовательно, задача имеет оптимальное решение.

Перейдем от исходного опорного решения Х₀ к лучшему Х_1.

В качестве ведущего столбца выберем столбец, в котором наибольшая по абсолютной величине отрицательная оценка ₁=-60, это первый столбец.

Для положительных элементов первого столбца составим симплексные отношения и запишем их в последнем столбце симплексной таблицы.

В качестве ведущей строки возьмем строку с минимальным симплексным отношением- это первая строка, так как

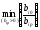==200,

таким образом, ведущий элемент b₁₁=2.

С этим ведущим элементом проведем одну итерацию метода Жордана- Гаусса, а именно:

• все элементы ведущей строки разделим на ведущий элемент

(на 2);

• в ведущем столбце все элементы кроме ведущего заменим нулями (запишем единичный столбец);

• элементы b₁₄=b₁₅=0, следовательно, четвертый и пятый столбцы останутся без изменения;

• все остальные элементы симплекс-таблицы преобразуем по правилу « определителя второго порядка »,

например, b₂₂=(2^.4 -1^.3): 2=5/2.

Итак, получим новую симплекс-таблицу:

Базис	х1	х2	х3	х4	х5	bi0	bi0 / bip
x1	1	1/2	1/2	0	0	200	400
x4	0	5/2	-3/2	1	0	300	120
x5	0	5/2	-1/2	0	1	400	160
f	0	-10	30	0	0	1200

Таким образом, полагая свободные переменные х₂=х₃=0, получим новое опорное решение Х₁=(200, 0, 0, 300, 400).

Значение целевой функции(см. в строке целевой функции) при опорном решении Х₁ равно

f(X₁)=1200.

Полученное решение Х₁ снова не оптимально, так как в последней строке таблицы - в строке целевой функции

оценка ₂=-10<0.

В столбце (втором) над этой оценкой есть положительные числа, следовательно, проведем еще одну итерацию с ведущим элементом b₂₂=5/2

(выбрали ведущую строку – вторую - по минимальному симплексному отношению==120).

В результате получим симплексную таблицу

Базис	х1	х2	х3	х4	х5	bi0	bi0 / bip
x1	1	0	4/5	-1/5	0	140
x2	0	1	-3/5	2/5	0	120
x5	0	0	1	-1	1	100
f	0	0	4	0	0	13200

Новое опорное решение найдем при свободных переменных х₃=х₄=0, получим Х₂=(140, 120, 0, 0, 100),

Значение целевой функции равно

f(X₂)=13200.

Так как в последней строке целевой функции нет отрицательных оценок, то найденное опорное решение оптимально, причем

х₁=140, х₂=120, х₃=х₄=0, х₅=100, f_max=13200.

Итак, задача решена, оптимальный план производства будет следующий:

нужно произвести 140 изделий типа А, 120 изделий типа В, которые обеспечат максимальную прибыль при их реализации в размере 13200 руб., причем будет экономия сырья третьего типа в количестве 100 кг.