1. Оптимизационные задачи, их классификация

   1. Классификация задач оптимизации

Оптимизационная задача задаётся тройкой , гдеF – функция, определённая на множестве , аD – некоторое подмножество множества .

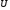Функция F называется целевой функцией;

D – множеством допустимых решений (допустимой областью)

оптимизационной задачи;

_{U- пространством оптимизации.}

Оптимизационная задача максимизации (минимизации) состоит в отыскании наибольшего (наименьшего) значения целевой функции F на допустимом множестве D.

Любая задача максимизации сводится к задаче минимизации.

Решить оптимизационную задачу – значит найти её оптимальное решение, либо установить неразрешимость этой задачи. Например, задача максимизации (минимизации) будет неразрешимой, если щелевая функцияF неограниченна сверху (снизу) на множестве D.

_{Методы решения оптимизационных задач зависят как от вида целевой функции} F, так и от вида множества допустимых решения D. _{- оптимизируемая целевая функция, или целевой функционал , критерий качества - численно выражает степень достижения целей функционирования оптимизируемого объекта. Целевая функция представляет собой набор критериев качества, которые должны быть оптимизированы одновременно. Соответственно, приk=1 имеем задачу однокритериальной или скалярной оптимизации, а при k>1 – задачу многокритериальной или векторной оптимизации.}

_{Вектор неизвестных может содержать одну компоненту (n=1) и тогда мы имеем задачу одномерной оптимизации, а может иметь и много составляющих (n>1) и тогда это задача многомерной оптимизации или задача оптимизации со многими переменными.}

_{Допустимая область D может совпадать с пространством оптимизации (D =U ), что означает отсутствие каких-либо ограничений на неизвестные. В этом случае имеем задачу безусловной оптимизации или задачу оптимизации без ограничений. Если же , то в задаче не все значения переменных допустимы, т.е. имеются некоторые ограничения на них. Соответствующая задача оптимизации называетсяусловной или задачей с ограничениями.}

_{Пространство оптимизации U может совпадать с евклидовым пространством и мы получаем задачу оптимизации с непрерывными переменными.}

_{Если переменные являются целочисленными, то соответствующая задача носит название целочисленной оптимизации. Частным случаем целочисленной оптимизации является булевая оптимизация, при которой переменные могут принимать только два значения – ноль и единица. Если при этом целевая функция принимает значения из множества вещественных чисел, то такая задача называется задачей псевдобулевой оптимизации, чтобы подчеркнуть ее отличие от случая, когда и значения функции тоже являются нулем или единицей.}

_{Если же значение целевой функции зависит от некоторых комбинаций объектов из конечного набора, их размещения или способа упорядочения, то такие задачи называются задачами комбинаторной оптимизации.}

_{Задачи целочисленной и комбинаторной оптимизации объединяются понятием задач дискретной оптимизации. Наконец, существуют задачи смешанной оптимизации, в которых могут одновременно присутствовать переменные всех типов. Наиболее известным случаем таких задач являются дачи смешанного целочисленного программирования с целочисленными и непрерывными переменными.}

_{Приведем классификацию задач оптимизации с учетом конкретной формы задачи и свойств функции, входящих в ее постановку, как это сделано в работе [15]}

_{Прежде всего целевая функция и функции, описывающие ограничения, могут быть заданы не аналитически, а в виде компьютерных программ, имитационных моделей, человеко-машинных процедур или даже как выход реальной системы. Такие задачи оптимизации называют задачами оптимизации с неявными функциями или поисковыми задачами оптимизации. Процесс оптимизации в таком случае больше похож на экспериментирование, чем на вычисление.}

_{Если же все функции, входящие в постановку задачи, записываются в явном аналитическом виде , то соответствующая задача оптимизации называется задачей математического программирования. Чаще всего математическим программированием называют задачи оптимизации с ограничениями, подчеркивая их отличие от задач безусловной оптимизации.}

В математическом программировании основными разделами являются: линейное программирование, целочисленное, выпуклое программирование.

Оптимизационная задача , в которой целевая функцияF является линейной функцией на , аD является множеством решений некоторой системы линейных уравнений и линейных неравенств от неизвестных, называетсязадачей линейного программирования. Систему линейных уравнений и неравенств, определяющую множество D , называют системой ограничений задачи линейного программирования.

_{Существуют более узкие постановки задачи линейного программирования – транспортная задача, задача о назначениях, задача целочисленного линейного программирования и другие.}

_{Если целевая функция сепарабельна, т.е. изменяется независимо по каждой переменной в отдельности, а ограничения – линейны, то задача называется задачей сепарабельного программирования.}

_{Если целевая функция квадратична, а ограничения – линейны, то задача называется задачей квадратичного программирования.}

_{Если целевая функция выпукла, а функции-ограничения образуют выпуклую допустимую область, то соответствующая задача носит название задачи выпуклой оптимизации.}

_{В случае функций общего вида говорят об общей задаче нелинейного программирования.}

_{Предполагалось также, что все функции и коэффициенты, входящие в постановку задачи являются постоянными величинами, а они могут на самом деле зависеть от некоторого параметра или параметров. В таком случае нужно изучать поведение оптимального решения при изменении исходных данных задачи, разрабатывать методы, позволяющие находить оптимальный план сразу для совокупности значений параметров. Соответствующие задачи получили название параметрических задач оптимизации, а этот раздел методов оптимизации называется параметрическим программированием.}

_{Наконец, до сих пор, опять таки неявно, предполагалось, что вся исходная информация определена однозначно. Такие задачи называются детерминированными. Такие модели могут оказаться неадекватными реальным процессам, которые могут характеризоваться неполнотой, неточностью данных, на основе которых формируется модель.}

_{В ситуациях, когда все или некоторые параметры модели носят вероятностный характер, говорят о принятии решения в условиях риска и соответствующие оптимизационные задачи называют стохастическими, а соответствующий раздел теории – стохастическим программированием или стохастической аппроксимацией.}

_{Однако неопределенность данных задачи может иметь и не вероятностный характер. В таких ситуациях говорят об оптимизации в условиях неопределенности. Методы решения в таких случаях основываются на теории нечетких множеств и так называемой нечеткой логике и объединяются под названием нечеткого математического программирования или нечеткой оптимизации.}