4. Симплекс- метод решения задач линейного программирования

Симплексный метод является наиболее применимым в настоящее время методом решения задач линейного программирования. Как известно, если задача линейного программирования имеет оптимальное решение, то оно совпадает, по крайней мере, с одним из опорных решений. Именно, на этом основана идея рассматриваемого метода - упорядоченный перебор опорных решений или последовательное их улучшение.

4.1 Метод Жордана – Гаусса - метод решения систем линейных уравнений

Метод последовательных исключений, или Жордана- Гаусса представляет собой удобный вычислительный алгоритм, построенный на последовательном применении эквивалентных преобразований системы линейных уравнений, которые приводят к равносильной системе.

Рассмотрим систему m уравнений с n неизвестными:

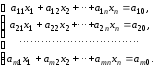
Алгоритм метода Жордана - Гаусса:

1. Все коэффициенты системы и свободные члены (элементы расширенной матрицы системы) записывают в таблицу

2. Выбирают ведущий элемент0 (k=1,2,...,m; s=1,2,...,n) ,

где k- тую строку называют ведущей, s- тый столбец - ведущим.

2. Все элементы ведущей строки пересчитывают по формуле:

т.е. элементы ведущей строки делятся на ведущий элемент.

В ведущем столбце элементы записывают нулями, кроме ведущего.

4. Остальные элементы таблицы пересчитывают по формуле «определителя второго порядка»:

,

полагая главной диагональю ту, где находится ведущий элемент:

и полученный результат всегда делится на ведущий элемент

(см. пример 7).

Итак, для любого элемента таблицы получим:

4. Следующая итерация проводится над элементами полученной таблицы. Все преобразования проводят до тех пор, пока система не будет приведена к единичному базису.

Систему r- уравнений, в которой столбцы коэффициентов при r неизвестных являются единичными векторами: e₁=(1,0,. . . ,0), e₂=(0,1,. . .,0), e_r=(0,0,. . .,1) называют системой уравнений, приведенной к единичному базису:

Очевидно, ранг системы равен r.

Выразив базисные переменные x₁,x₂,…,x_r через свободные x_r+1,x_r+2,…,x_n, получим общее решение системы линейных уравнений:

Замечания:

1. Если число r базисных неизвестных равно n- числу неизвестных системы, т.е. r=n то система имеет единственное решение:

X=( ,,,. . .,)

2. Если в ходе вычислений появится строка таблицы, все элементы которой, кроме свободного члена, равны нулю, то данная система несовместна.

1. Если r<n (число базисных переменных меньше числа всех неизвестных), то система не определена и находим общее решение.

2. Если в общем решении неопределенной системы линейных уравнений свободным неизвестным придать нулевые значения, то полученное частное решение X=(b₁₀; b₂₀; . . .; b_r0; 0; 0; . . .; 0), называется базисным.

Неотрицательные базисные решения системы называются опорными.

Базисное решение не единственно ,так как выбор ведущего элемента произволен. Система m уравнений с n неизвестными, у которой ранг (число базисных переменных) равен r, может иметь различных базисных решений не более, чем

Пример 7 Найти методом Жордана - Гаусса общее решение, а также все базисные и опорные решения следующей системы линейных уравнений:

Решение

Согласно алгоритму метода Жордана - Гаусса все коэффициенты системы и свободные члены (элементы расширенной матрицы системы) запишем в таблицу, в которой и выполним все преобразования (подробный комментарий к каждой итерации приводится после таблицы):

Базис	х1		х2	х3	х4	аi0
х1	1		-2	0	1	-3	ведущая строка
	3		-1	-2	0	1
	2		1	-2	-1	4
	1		3	-2	-2	7
I итерация
х1	1		-2	0	1	-3
х2	0		5	-2	-3	10	ведущая строка
	0		5	-2	-3	10
	0		5	-2	-3	10
II итерация
х1		1	0	-4/5	-1/5	1
х2		0	1	-2/5	-3/5	2
		0	0	0	0	0
		0	0	0	0	0

1. Выбран ведущий элемент а₁₁=1 в первой таблице, составленной по условию задачи.

I итерация:

2. Вторую таблицу начинают заполнять с элементов ведущей строки (она не изменилась)

3. В первом столбце записывают нули, кроме а₁₁=1.

4. а₁₃=0, следовательно, третий столбец не изменится.

5. Вычисление остальных элементов производят по формуле « определителя второго порядка »:

После окончания I итерации получаем в первом столбце (1,0,0,0) и базисную переменную х₁.

II итерация:

1. Выбран в качестве ведущего элемента а₂₂=5.

2. Элементы ведущей строки делят на 5.

3. Во втором столбце записывают нули, кроме а₂₂=1

4. Вычисление остальных элементов производят по формуле «определителя второго порядка». После итерации I получили три совпадающих строки, откуда следует, что два уравнения «лишние». При выполнении итерации II эти строки превратились в нулевые строки. В результате получаем два уравнения (ранг r=2), которые разрешены относительно базисных переменных х₁ и х₂.

Таким образом, данная система совместна и не определена, ее общее решение имеет вид:

Частное решение Х=(1,2,0,0) - базисное решение. Всего базисных решений будет шесть, так как

.

Чтобы найти остальные базисные решения, проводим «замещение» одной базисной переменной на другую, до тех пор пока не найдем все базисные решения системы. Следует при этом следить, чтобы на какой-то итерации не повторялся уже использованный ранее базис.

Базис	х1	х2	х3	х4	bi0	Базисные решения
x1	1	0	-4/5	-1/5	1	(1,2,0,0)
x2	0	1	-2/5	-3/5	2
I итерация
x3	-5/4	0	1	1/4	-5/4	(0,3/2,-5/4,0)
x2	-1/2	1	0	-1/2	3/2
II итерация
x3	0	-5/2	1	3/2	-5	(-3,0,-5,0)
x1	1	-2	0	1	-3