5.1 Постановка двойственной задачи

Экономическая постановка и математическая модель каждой из этих задач следующие:

Задача P: об использовании сырья (прямая задача)

Для производства видов продукциифирма может использоватьвидов сырья, запасы которых соответственно равны. Известны нормы расхода каждого из ресурсов на единицу продукции, обозначим. Прибыль от реализации единицы продукцииобозначимусловных единиц. Требуется найти оптимальный план производства продукции, чтобы при заданных условиях, суммарная прибыль, полученная от реализации всей продукции, была бы максимальной.

Математическая модель задачи P следующая:

пусть x количество продукции, очевидно, что

.

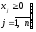Расходы ресурсов не должны превышать их запасы, таким образом, должны выполняться следующие ограничения

.

Целевая функция данной задачи есть суммарная прибыль от реализации всей продукции, она равна

.

Итак, надо найти такой план производства , при котором целевая функция достигает максимума, причем выполнялись бы условия:

Двойственной задачи о ресурсах (задача D)

Экономическая постановка:

фирма заинтересована получить доход от продажи ресурсов , причем доход должен быть не меньше того, который был бы получен при продаже готовой продукции.

Покупатель, стремится приобрести ресурсы по минимальной стоимости.

Требуется найти оптимальные оценки ресурсов (их относительные цены).

Математическая модель задачи D:

пусть - оценки единицы ресурсов, их относительные цены; очевидно, что.

Доход фирмы, который она получит от продажи всех ресурсов , необходимых для производства единицы продукции вида, равен сумме произведений норм расхода сырья на цену единицы каждого ресурса:

.

Чтобы доход от продажи ресурсов был не меньше, чем доход от реализации изготовленной из них продукции, должны выполняться неравенства:

Целевая функция этой задачи есть затраты фирмы – покупателя, она равна

Итак, надо найти , при котором затраты будут минимальными, причем выполняются условия неотрицательности и ограничения:и.

Сравнивая прямую и двойственную к ней задачи, отметим следующее:

1) одна из задач является задачей максимизации, другая – задачей минимизации;

2) в задаче максимизации все неравенства – типа «», в задаче минимизации – типа «»;

3) число неизвестных одной задачи равно числу неравенств другой;

4) матрица из коэффициентов при неизвестных в исходной задаче , а аналогичная матрица в двойственной задаче

получена транспонированием исходной (т.е. заменой строк столбцами);

5. свободные члены неравенств одной из задач равны коэффициентам при соответствующих неизвестных в выражении целевой функции другой задачи.

Замечание

Задачи P и D называют симметричными взаимодвойственными.

К двойственному методу удобно прибегать тогда, когда в исходной задаче число ограничений значительно больше числа неизвестных.

При решении задач линейного программирования на ЭВМ объем вычислений определяется в большей степени числом неизвестных, поэтому обращение к двойственной задаче оказывается полезным.

Пример 14

Найти оптимальное решение, при которомдостигает минимума и выполняются условия:

.

Решение

Запишем условие прямой задачи P и составим двойственную к ней задачу D, решим графически обе задачи.

Задача P	Задача D
Вектор-градиент	Вектор-градиент
Оптимальное решение	Оптимальное решение

Рис.5