7.5 Статистические игры

Статистической игрой (игрой с природой) называется парная матричная игра, в которой один из участников (второй игрок) не заинтересован в исходе игры; а первый игрок – «статистик» - должен принимать решение в условиях неопределенности. Другими словами сознательный игрок («статистик»), заинтересованный в наиболее выгодном для него исходе игры, выступает против участника, совершенно безразличного к результату игры. Оптимальную стратегию статистика можно определить, используя ряд критериев, которые опираются как на платежную матрицу, так и на, так называемую, матрицу рисков, которая позволяет более четко выявить преимущества одной стратегии по сравнению с другой при данном состоянии природы.

Риском первого игрока, применяющего i-ую стратегию, называется разность между его максимально возможным выигрышем, соответствующим известному j–му состояниюприроды, и его реальным выигрышем в случае, когдаj–ое состояние природы неизвестно. Величину риска находят по формуле

, где –наибольший элемент в каждом столбце платежной матрицы.

Пример 26

Известна платежная матрица статистической игры:

Составить матрицу рисков.

Решение Найдем наибольший элемент в каждом столбце платежной матрицы:

Теперь вычислим риски первого игрока, применяющего одну из трех возможных стратегий: для этого найдем разности

для элементов каждого столбца.

Для первого столбца	Для второго столбца	Для третьего столбца	Для четвертого столбца

Итак, матрица рисков имеет вид:

При нахождении оптимальных решений статистических игр используют

следующие критерии:

1. Если вероятности состояний природы известны, то для нахождения оптимальных стратегий статистика применяют критерии Байеса и Лапласа.

Критерий Байеса

Показателем оптимальности стратегии статистика служит либо величина выигрыша, либо величина среднего риска.

Показатель оптимальности стратегии – величина среднего выигрыша. За оптимальную принимается чистая стратегия, при которой максимизируется средний выигрыш статистика

.

Показатель оптимальности стратегии – величина среднего риска. За оптимальную стратегию принимается чистая стратегия, при которой минимизируется средний риск

.

Заметим, что стратегия, максимизирующая средний выигрыш, совпадает со стратегией, минимизирующей средний риск.

Критерий Лапласа

Если состояния природы в равной мере правдоподобны, то их полагают равновероятными, т.е..

Показатель оптимальности стратегии – величина среднего выигрыша. Оптимальной считается чистая стратегия, обеспечивающая максимум среднего выигрыша при одинаковых априорных вероятностях:

,

где

2. Если вероятности состояний природы неизвестны, то для выбора оптимальной стратеги статистика, применяют критерии Вальда, Сэвиджа и Гурвица.

Критерий Вальда – максиминный критерий.

Критерий Вальда является критерием крайнего пессимизма, так как статистик предполагает, что природа реализует такие состояния, при которых величина его выигрыша принимает наименьшее значение.

Оптимальный по критерию Вальда считается чистая стратегия, которая в наихудших условиях гарантирует максимальный выигрыш

.

Значит, оптимальной будет максиминная чистая стратегия, а максимальным выигрышем – нижняя чистая цена игры в парной игре с нулевой суммой.

Для смешанных стратегий критерий Вальда формулируется так:

Оптимальной считается та смешанная стратегия статистика

Х = (), при которой минимальный средний выигрыш будет максимальным

.

Критерий Вальда ориентирует статистика на самые неблагоприятные состояния природы, то есть выражает пессимистическую оценку ситуации.

Критерий Сэвиджа - максиминный критерий.

Оптимальной стратегией является та, при которой минимизируется величина максимального риска

Критерий Сэвиджа, как и критерий Вальда, ориентирует статистика на самые неблагоприятные состояния природы.

Критерий Гурвица – критерий пессимизма – оптимизма.

Оптимальной является та чистая стратегия, для которой выполняется соотношение

,

где число называетсякоэффициентом доверия, удовлетворяет условию и выбирается из субъективных соображений или исходя из опыта.

При =0 имеем критерий крайнего оптимизма, а при=1 получим критерий крайнего пессимизма Вальда.

Оптимальная по Гурвицу стратегия должна гарантировать статистику больший выигрыш в сравнении с выигрышем по стратегии, которую статистик выбирает интуитивно или исходя из опыта.

На практике при нахождении оптимального решения применяют ни один, а несколько критериев.

Пример 27

Найти оптимальное решение статистической игры, заданной платежной матрицей, применяя критерий Байеса, считая, что вероятности состояний природы известны и равновероятны.

Решение Положительные элементы в платежной матрице означают, что игрок 1 выигрывает у природы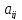условных единиц. Отрицательные элементы показывают, что игрок 1 несет затратыусловных единиц.

Для применения критерия Байеса нужно знать вероятности состояний, но условно, они вероятны тогдаприроды, теперь найдем средние выигрышиигрока 1 по формуле:

;

;

;

Оптимальной стратегией статистика игрока 1 является чистая третья стратегия, поскольку ей соответствует максимальный средний выигрыш:

Применим в качестве показателя оптимальности величину среднего риска. Найдем риски статистика:

,

,

,

,

,

,

,

,

.

Вычислим для каждой стратегии средний риск:

;

;

;

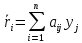
Найдем наименьший риск:

Итак, оптимальной стратегией является третья.

Пример 28

Найти оптимальные решения статистической игры, если вероятности состояний природы неизвестны. Игра задана платежной матрицей

A=

Решение

Для нахождения оптимальной стратегии применим следующие критерии:

1. Критерий Лапласа.

При неизвестных вероятностях состояний природы, полагают, что состояния равновероятны, то есть .

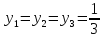Тогда, средние выигрыши равны:

Итак, оптимальной стратегией будет третья.

2. Критерий Вальда.

Вычислим минимально возможные выигрыши игрока 1 для каждой его стратегии.

Тогда, наибольший выигрыш из минимально возможных равен:

Итак, оптимальной стратегией по критерию Вальда также является третья.

3. Критерий Сэвиджа.

Построим матрицу рисков (Пример 26)

, где

- наибольший элемент в каждом столбце платежной матрицы

,

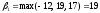(8,-11,-9)=8,

(14,-10,13)=14,

тогда матрица рисков равна

Найдем средние риски

,

,

.

Тогда, наименьший средний риск равен:

Итак, оптимальной стратегией также является третья стратегия.

4. Критерий Гурвица

,

Положим, что коэффициент доверия – это вероятность возможного выигрыша игрока 1.

Вычислим для каждой стратегии игрока 1

Далее найдем

Таким образом, и по критерию Гурвица третья стратегия является оптимальной.