
- •1.Оптимизационные задачи, их классификация 7
- •Оптимизационные задачи, их классификация
- •Классификация задач оптимизации
- •Классификация методов оптимизации
- •2. Постановка задачи линейного программирования
- •2.1 Общая задача линейного программирования (злп)
- •2.2 Математические модели задач линейного программирования
- •2.3 Формы записи задач линейного программирования: общая, каноническая и стандартная
- •3. Графический метод решения задачи линейного программирования
- •4. Симплекс- метод решения задач линейного программирования
- •4.1 Метод Жордана – Гаусса - метод решения систем линейных уравнений
- •III итерация
- •4.2. Симплексные таблицы. Нахождение начального опорного решения
- •4.3. Критерий оптимальности
- •4.4. Невырожденные злп, алгоритм их решения
- •4.5. Альтернативный оптимум, алгоритм нахождения всех оптимальных решений
- •Алгоритм нахождения всех оптимальных опорных решений
- •4.6. Вырожденные злп, алгоритм их решения
- •5. Двойственные задачи
- •5.1 Постановка двойственной задачи
- •5.2 Основное неравенство двойственности
- •5.3 Критерий Канторовича
- •5.4 Первая теорема двойственности
- •5.5. Вторая теорема двойственности (необходимое и достаточное условия оптимальности решения).
- •5.6. Третья теорема двойственности
- •5.7. Двойственный симплекс-метод
- •6. Транспортная задача
- •6.1 Экономическая постановка и математическая модель транспортной задачи
- •6.2 Методы нахождения начального плана перевозок
- •Метод «северо-западного угла»
- •Метод минимальной стоимости
- •6.3 Метод потенциалов решения транспортной задачи
- •6.4 Открытая модель транспортной задачи
- •7. Матричные игры, их применение к решению оптимизационных задач
- •7.1 Основные понятия теории матричных игр
- •7.2 Решение матричных игр в чистых стратегиях
- •7.3 Решение матричной игры в смешанных стратегиях
- •7.4 Сведение матричной игры к задаче линейного программирования
- •7.5 Статистические игры
- •8. Графы, их применение в решение оптимизационных задач
- •8.1 Определение графа
- •8.2 Путь и цикл в графе
- •8.3 Связность графа, деревья
- •8.4 Виды графов
- •8.5 Сети. Критический путь
- •Вопросы к экзамену
- •Индивидуальные задания Задание 1
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Задание 6
- •Задание 7
- •Задание 8
- •Задание 9 Задачи 9.1 – 9.10
- •Методы оптимизации
- •Часть I
Метод минимальной стоимости
Идея
этого метода заключается в том, чтобы
заполнить клетки таблицы, начиная с
клетки с наименьшей стоимостью
 .
.
Этот метод, как правило, позволяет получить более «выгодный» план, чем метод «северо-западного угла».
Пример 19
Найти
начальный план перевозок методом
минимальной
стоимости, если
груз находится у трех поставщиков в
количествах 120, 85 и 135 единиц, который
необходимо доставить потребителям в
количествах 50, 90, 110 и 90 единиц, причем
стоимость транспортировки единицы
продукции от
 -го
поставщика в пункт потребления
-го
поставщика в пункт потребления
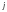 задана
матрицей:
задана
матрицей:

Решение
Решение найдем методом минимальной стоимости:
|
Потребители
Поставщики
|
50 |
90 |
110 |
90 |
|
120 |
5
|
11 70 |
10
|
8 |
|
85 |
10
|
8 20 |
4
|
2 65 |
|
135 |
9
|
7 |
1 110 |
5 25 |
Итак, начальный план перевозок следующий
 ,
,
причем суммарная стоимость затрат на перевозки равна:
Z(X)_= 1445
6.3 Метод потенциалов решения транспортной задачи
Общий принцип определения оптимального плана транспортной задачи методом потенциалов аналогичен принципу решения задачи линейного программирования симплексным методом, а именно:
сначала находят начальный опорный план перевозок
 ,
,затем переходят к новому плану
 ,
лучшему, такому, что
,
лучшему, такому, что
Z( )
≤Z(
)
≤Z( )
)
проверяют критерий оптимальности полученного решения:
Если для некоторого опорного плана

транспортной
задачи существуют такие числа

 ,
что
,
что
 ,
,
 ,
,
то
 есть
оптимальный
план транспортной
задачи
есть
оптимальный
план транспортной
задачи
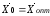 .
.
Числа
 называются
потенциалами
соответственно
пунктов поставки и пунктов потребления.
называются
потенциалами
соответственно
пунктов поставки и пунктов потребления.
Критерий оптимальности решения транспортной задачи следующий:
для
того чтобы
решение
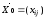 было
оптимальным, необходимо и
было
оптимальным, необходимо и
достаточно,
чтобы
существовала система
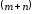 чисел
чисел
 ,
,
которые удовлетворяли бы условиям:
 для
всех базисных переменных (занятых
клеток) и
для
всех базисных переменных (занятых
клеток) и
 для
всех свободных переменных (пустых
клеток).
для
всех свободных переменных (пустых
клеток).
Алгоритм метода потенциалов решения транспортной задачи
Найти начальный план перевозок транспортной задачи
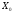 методом
«северо-западного угла»
или методом минимальной стоимости.
Число
заполненных клеток должно быть равным
методом
«северо-западного угла»
или методом минимальной стоимости.
Число
заполненных клеток должно быть равным
 .
.Найти
 .
.
Найти потенциалы
 из
системы уравнений:
из
системы уравнений:
 ,
составленной для занятых клеток.
,
составленной для занятых клеток.Найти оценки
 для
свободных клеток:
для
свободных клеток:
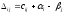 .
.Если среди чисел
 нет
отрицательных
значений, все
нет
отрицательных
значений, все ,
то найденный опорный план
,
то найденный опорный план является
оптимальным.
является
оптимальным.Если же для некоторой свободной клетки
 ,
то исходный опорный план не
является оптимальным и необходимо
перейти к новому опорному плану
,
то исходный опорный план не
является оптимальным и необходимо
перейти к новому опорному плану
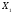 ,
причем
,
причем
Z( )
≤Z(
)
≤Z(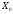 )
)
Чтобы решение
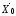 улучшить, выбирают среди отрицательных
оценок
улучшить, выбирают среди отрицательных
оценок наибольшую по абсолютной величине (при
нескольких равных выбирают
любую) и для соответствующей свободной
клетки строим
цикл
пересчета.
наибольшую по абсолютной величине (при
нескольких равных выбирают
любую) и для соответствующей свободной
клетки строим
цикл
пересчета.
Цикл – это замкнутая ломаная, соединяющая несколько занятых клеток таблицы. Две последовательные вершины цикла лежат либо в одной строке, либо в одном столбце; в одной их них объем увеличивается (в клетке ставится знак «+»); в другой – уменьшается настолько же единиц (в клетке ставится знак «–»).
7. Среди клеток, имеющих знак «–» отыскивается та, которая содержит минимальную величину поставки. Эта величина прибавляется к содержимому клеток, имеющих знак «+» и вычитается из содержимого клеток, имеющих знак «–».
8. Для
нового опорного плана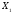 заново
рассчитываются потенциалы
заново
рассчитываются потенциалы ,
, и
оценки(п.3)
и
оценки(п.3)
Замечание
Потенциалам
 и
и
 можно
придать простой экономический смысл:
можно
придать простой экономический смысл:
 –
стоимость единицы
груза для
–
стоимость единицы
груза для
 -го
поставщика,
-го
поставщика,
 – стоимость
единицы груза у
– стоимость
единицы груза у
 -ого
потребителя.
-ого
потребителя.
Если
для некоторой свободной
клетки величина
 т.е.
т.е.
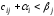 .
Это
означает,
что перевозки из пункта
.
Это
означает,
что перевозки из пункта
 в
пункт
в
пункт целесообразны, потому чтоони
приведут к уменьшению стоимости единицы
груза в пункте назначения, а переменную
целесообразны, потому чтоони
приведут к уменьшению стоимости единицы
груза в пункте назначения, а переменную
 нужно
внести в базис. В то же время равенство
нужно
внести в базис. В то же время равенство
 для базисных переменных (занятых клеток)
означает, что
перевозки, внесенные в план, должны быть
«безубыточными», а стоимость груза
в пункте отправления плюс издержки
для базисных переменных (занятых клеток)
означает, что
перевозки, внесенные в план, должны быть
«безубыточными», а стоимость груза
в пункте отправления плюс издержки
 на
перевозку должны в точности
покрываться стоимостью груза в
пункте
потребления.
на
перевозку должны в точности
покрываться стоимостью груза в
пункте
потребления.
Пример 20
Найти
оптимальный план перевозок, при котором
суммарная стоимость всех перевозок –
наименьшая,
если
груз находится у трех поставщиков в
количествах 12
, 8 и 10 единиц, который необходимо
доставить потребителям в количествах
6, 9 , 15
единиц, причем
стоимость транспортировки единицы
продукции от
 -го
поставщика в пункт потребления
-го
поставщика в пункт потребления
 задана
матрицей:
задана
матрицей:

Решение
Составим математическую модель задачи.
Обозначим:
 –количество
единиц груза перевозимого от i-ого
поставщика отправления к j-у
потребителю
–количество
единиц груза перевозимого от i-ого
поставщика отправления к j-у
потребителю
Условия задачи запишем в таблицу
|
Потребители
Поставщики
|
6 |
9 |
15 |
|
12 |
1
|
3
|
4
|
|
8 |
2
|
5
|
3
|
|
10 |
6
|
7 |
5
|
Так
как
 ,
то транспортная задача – закрытая. На
искомые
перевозки xij
по
смыслу задачи необходимо наложить
следующие условия:
,
то транспортная задача – закрытая. На
искомые
перевозки xij
по
смыслу задачи необходимо наложить
следующие условия:
а)
условия по запасам:
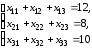 ;
;
б)
условия по потребностям:
 ;
;
в)
условия неотрицательности:
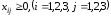 .
Транспортные
расходы при таком плане перевозок
составят:
.
Транспортные
расходы при таком плане перевозок
составят:
 .
.
Начальный план перевозок найдем методом северо-западного угла:
|
Потребители
Поставщики
|
6 |
9 |
15 |
|
12 |
1
|
3 6 |
4
|
|
8 |
2
|
5 3 |
3 5 |
|
10 |
6
|
7 |
5 10 |
В результате получаем начальный опорный план

Переменные, стоящие в занятых клетках таблиц, являются базисными, а остальные ( в пустых клетках) – свободными.
Полученный план перевозок является допустимым, т.к. удовлетворяет ограничениям задачи. Это выражается в том, что сумма объемов перевозок в каждом столбце равна потребностям; а в строке запасам. Согласно данному плану перевозок, общая стоимость перевозок всего груза составляет:
 =1∙6+3∙6+5∙3+3∙5+5∙10=104
=1∙6+3∙6+5∙3+3∙5+5∙10=104
Найдем
потенциалы
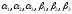 из
системы уравнений:
из
системы уравнений:
 ,
составленной для занятых клеток,
очевидно, что
,
составленной для занятых клеток,
очевидно, что


Поскольку
количество неизвестных шесть и
на
единицу превышает число уравнений
в системе (пять занятых клеток), то одно
из неизвестных (обычно) принимаем за
нуль,
например,
a1=0,
тогда потенциалы остальных строк и
столбцов однозначно определяются:
 .
.
Запишем их в таблице:
|
Потребители
Поставщики
|
6 |
9 |
15 |
|
|
12 |
1
|
3 6 |
4
|
|
|
8 |
2 |
5 3 |
3 5 |
|
|
10 |
6
|
7 |
5 10 |
|
|
|
|
|
|
|
Найдем
оценки для свободных переменных (пустых клеток)
из системы уравнений:
для свободных переменных (пустых клеток)
из системы уравнений:
 .
.

Оценка
 отрицательная,
следовательно, решение
отрицательная,
следовательно, решение
 не
является оптимальным,
а значение целевой функции
не
является оптимальным,
а значение целевой функции
 =
104 можно уменьшить.
=
104 можно уменьшить.
Построим
цикл.
Так как оценка
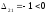 ,
то переменную x21
введем
в базис (клетку (2,1)
сделаем
занятой). В эту клетку запишем число
,
то переменную x21
введем
в базис (клетку (2,1)
сделаем
занятой). В эту клетку запишем число
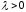 .
Сумма перевозок по строкам и столбцам
таблицы должна оставаться неизменной,
необходимо восстановить баланс каждой
строки и столбца. Будем прибавлять
или вычитать
.
Сумма перевозок по строкам и столбцам
таблицы должна оставаться неизменной,
необходимо восстановить баланс каждой
строки и столбца. Будем прибавлять
или вычитать
 из переменных, записанных в базисных
клетках.Для
свободной клетки (2,1)
можно построить единственный цикл
пересчета: (2,1),
(1,1), (1,2), (2,2),(2,1)
из переменных, записанных в базисных
клетках.Для
свободной клетки (2,1)
можно построить единственный цикл
пересчета: (2,1),
(1,1), (1,2), (2,2),(2,1)
Если соединить последовательно клетки цикла отрезками прямой, то получится замкнутая ломаная линия, каждый отрезок которой лежит либо в строке, либо в столбце, и только одна из вершин этой ломаной лежит в свободной клетке, т.е. в клетке (2,1),
Запишем
в клетку (2,1),)
число
 и
поставим знак «+», в соседних с ней
вершинах цикла поставим знак «-»,
и
поставим знак «+», в соседних с ней
вершинах цикла поставим знак «-»,
|
Потребители
Поставщики
|
6 |
9 |
15 |
|
12 |
  - 1 6 |
 + 3 6 |
4
|
|
8 |
2 
|
5 3 - |
3 5 |
|
10 |
6
|
7 |
5 10 |
Число
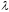 выбираем наименьшим
из чисел, находящихся в «отрицательных»
клетках:
выбираем наименьшим
из чисел, находящихся в «отрицательных»
клетках:
 .
.
Свободная клетка (2,1) стала занятой.
Итак, перешли к новому опорному решению
|
Потребители
Поставщики
|
6 |
9 |
15 |
|
12 |
1
|
3 9 |
4
|
|
8 |
2
|
5
|
3 5 |
|
10 |
6
|
7 |
5 10 |

Затраты
на перевозки по плану
 составляют:
составляют:

Проверим
решение
 на оптимальность, применяя алгоритм
метода потенциалов.
на оптимальность, применяя алгоритм
метода потенциалов.
Найдем
потенциалы
 из
системы:
из
системы:
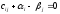 ,
,
составленной для занятых клеток, очевидно, что


Запишем в таблице найденные потенциалы
|
Потребители
Поставщики |
6 |
9 |
15 |
|
|
12 |
1
|
3 9 |
4
|
|
|
8 |
2 3 |
5
|
3 5 |
|
|
10 |
6
|
7 |
5 10 |
|
|
|
|
|
|
|
Вычислим
оценки
 для свободных переменных:
для свободных переменных:

Все
оценки
 свободных переменных неотрицательны.
Следовательно, решение
свободных переменных неотрицательны.
Следовательно, решение – оптимальное.
– оптимальное.
При
этом затраты на перевозку будут
минимальными:
 .
.
Дадим экономическое истолкование оптимального решения данной задачи:
для того, чтобы затраты на перевозку груза от потребителей
к поставщикам были наименьшими и равными 101 ед. стоимости, необходимо отправить
от первого поставщика 3 ед. груза и 9 ед. груза
соответственно первому и второму потребителю;
от второго поставщика 3 ед. груза и 5 ед. груза
соответственно первому и третьему потребителю;
от третьего поставщика 10 ед. груза третьему
потребителю.



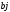




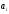
 =0
=0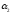 =-2
=-2 =-4
=-4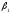 =1
=1 =3
=3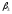 =1
=1

 +
+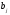



 =0
=0 =
-1
=
-1 =
-3
=
-3 =1
=1 =3
=3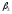 =2
=2