– наиболее комфортная для самочувствия человека принимается за среднюю.

m(x)

1

Рис. 1.16

– несомненно низкая, когда следует включить обогреватель.

– слишком высокая, когда требуется включить кондиционер. При температура относится одновременно к двум термам и воз-

никает проблема, какое решение принять.

1.12. Операции над нечёткими множествами

для всех . Операция нахождения минимума ткже обозна ается знаком , т. е.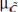

Рис. 1.17

18

, .

1.13. Параметры нечётких множеств

Высотой нечёткого множества называется верхняя граница его функции принадлежности. Для дискретного множества супре-

мум соответствует максимуму степеней принадлежности его элементов. Нечёткое множество называется нормальным, если его высота равна

единице, в противном случае множества называются субнормальными. Нормализация – преобразование субнормального нечёткого множества

в нормальное . Определяется следующим образом

На рис 1.19 показана нормализация нечёткого множества .

Ядром нечёткого множества называется чёткое подмножество универсального множества , элементы которого имеют степени принадлежности, равные 1.

Ядро субнормального нечёткого множества пустое.

19

a −сечением нечёткого множества называется чёткое подмножество универсального множества , элементы которого имеют степени принадлежности большие или равные

m(x)

mA% (x)

mA%¢(x)

Рис. 1.19

Носителем нечёткого множества 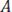называется чётное подмножество универсального множества , элементы которого имеют ненулевые степени принадлежности. (англ: support – носитель).

Ядро, a – сечение и носитель показаны на рис. 1.20.

20

Кардинальное число (или мощность) нечёткого множества равно сумме степеней принадлежности всех элементов к этому множеству

1.14. Методы дефаззификации нечётких множеств

Дефаззификация – процедура преобразования нечёткого множества в чёткое число. Простейший способ, пригодный только для одноэкстремальных функций принадлежности, заключается в выборе чёткого числа , соответствующего максимуму функции принадлежности.

Метод центра тяжести. Дефаззификация осуществляется по формуле (для дискретного универсального множества ).

i=1

Пример: Провести дефаззификацию нечёткого множества«мужчина среднего роста», заданного следующим образом

Результат дефаззификации имеет вид

Для непрерывного универсального множества – процедура находит центр тяжести плоской фигуры, ограниченной осями координат и графиком функции принадлежности 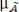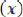в соответствии с выражением

b

ò x × mA% (x)dx

a

Метод медианы. Дефаззификация нечёткого множества 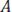по методу медианы состоит в нахождении такого числа , что

21