Решение уравнения (7.9) имеет вид
Выходной сигнал 
находится как решение алгебраического уравнения.
7.11. Представление уравнений состояния при помощи матриц
Если линейная стационарная система описывается дифференциальным уравнением 
-го порядка, то ее математическая модель в параметрах пространства состоя-
ний имеет вид
где 
– вход; 
– выход; 
– переменные состояния; 
, 
, C, 
– матрицы постоянных коэффициентов.
Будем рассматривать линейные системы с одним входом и одним выходом. Для системы 
-го порядка 
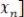вектор состояния, т. е. количество переменных состояния равно порядку системы. Рассмотрим систему, описываемую дифференциальным уравнением второго порядка
Необходимо описать систему в параметрах пространства состояний. Для построения схемы моделирования линейного дифференциального
уравнения любого порядка, необходимо последовательно проинтегрировать наивысшие производные уравнения, получить все производные низшего порядка и саму переменную 
.
Выразим
Количество интеграторов равно порядку системы и равно двум. Система замыкается исходя из условия удовлетворения дифференциальному уравнению
(рис. 7.14).
В качестве переменных состояния удобно выбрать выходы интеграторов:
. Тогда можно перейти к следующей системе уравнений:
(7.12)
147
u |
|
∫ |
|
|
+ |
∑ |
∫ |
y |
|
- |
||||
|
|
|
|
|
- |
|
|
|
|
Рис. 7.14. Схема моделирования системы второго порядка.
Систему (7.12) можно записать в матричном виде:
(7.13)
где |
. |
Таким образом, введение переменных состояния позволяет линейное дифференциальное уравнение второго порядка представить в виде системы двух дифференциальных уравнений первого порядка.
Рассмотрим обобщение методики на систему, описываемую дифференциальным уравнением n-го порядка
Коэффициент при высшей производной по y всегда можно привести к единице. Предположим вначале, что все 
, 
и только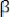 
. Введем переменные состояния следующим образом:
и выразим высшую производную из (7.14). Тогда
148
Переходя к системе уравнений первого порядка, получим
Схема моделирования, соответствующая системе уравнений (7.15) изображена на рис. 7.15.
u
+ |
∑ |
∫ |
∫ |
∫ |
∫ |
- |
|||||
- |
|||||
- |
|
|
|
|
|
Рис. 7.15 . Схема моделирования системы n-го порядка |
|
||||
Систему уравнений (7.15) можно представить в матричном виде следующим образом
Здесь матрица 
коэффициентов при x в дифференциальных уравнениях имеет вид
149
и называется матрицей Фробениуса. Элементы этой матрицы, расположенные над главной диагональю – единицы, элементы нижней строки – коэффициенты левой части дифференциального уравнения, взятые с противоположным знаком, все остальные элементы – нули.
Вектор строка C имеет только один единичный элемент, остальные нули. Если в уравнении (7.14) все 
отличны от нуля и порядок 
в левой и правой части одинаковый (т.е. 
), то вид матриц 
и 
остается таким же, а матрицы
D и |
вычисляются по следующим рекуррентным соотношениям |
Рассмотренная форма уравнений состояния, в которой матрица 
является матрицей Фробениуса, называется нормальной формой уравнения состояния.
Пример 7.4. Дифференциальное уравнение системы имеет вид
Привести уравнение к нормальной форме уравнений состояния, изобразить схему моделирования.
Матрица не требует вычислений и имеет вид |
мат- |
рица C = (1 0 0).
Найдем элементы матриц B и D:
Соответствующие уравнения состояния и имеют вид:
.
150
, где 
– вектор переменных состояния. Решение этого уравнения запишем по аналогии с выражением(7.11) для системы первого порядка
– матричная экспоненциальная функция, ее принято обозначать как 
. 
– квадратная матрица порядка 
, которая называется фундаментальной матрицей или переходной матрицей состояния. Матрица 
обладает следующими свойствами:
(единичная матрица),
,
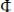
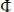
, если 
является промежуточным состоянием между 
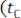
и 
Полагая 
, выражение (7.16) перепишем следующим образом
где первое слагаемое определяет свободную составляющую решения, зависящую от начальных условий, а второе – вынужденную составляющую, зависящую от входного сигнала.
Одним из способов вычисления матрицы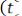 
является ее представление в виде ряда по степеням матрицы 
:
Число членов ряда при решении конкретной задачи определяется порядком системы n. Неизвестные коэффициенты 
определяются путем решения матричного уравнения
, |
(7.17) |
где 
– характеристические числа матрицы A, которые вычисляются путем решения уравнения 
.
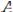
Определитель матрицы коэффициентов в левой части уравнения (7.17) носит название определителя Вандермонда.
Пример 7.5. Вычислить |
, если |
. Размер матрицы |
A определяет количество членов ряда |
|
. |
Найдем характеристические числа матрицы A, как корни уравнения
.
Далее решаем матричное уравнение
.
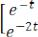
Перемножив матрицы в левой части и учитывая равенство векторов, получим систему уравнений
Решение системы имеет вид: 
, 
.
152
Следовательно
.
7.13. Характеристическое уравнение. Модальная матрица. Преобразование подобия
Если разомкнутая система n-го порядка задана передаточной функцией
вида
то полином 
называется характеристическим полиномом разомкнутой системы, а алгебраическое уравнение n-й степени 
, где 
некоторая переменная, называется характеристическим уравнением разомкнутой системы
Обозначим через 
корни характеристического уравнения (7.18). Если та же система задана уравнениями состояния
то характеристическое уравнение для |
такой модели можно записать как |
, где E – единичная матрица, |
– скалярная величина. |
Раскладывая определитель, получим уравнение вида
(7.19)
Значения 
, удовлетворяющие этому уравнению, называются характеристическими числами матрицы A, или ее собственными значениями. Уравнения (7.18) и (7.19) совпадают, так как речь идет об одной и той же системе.
Если матрица A имеет форму Фробениуса, которая была рассмотрена ранее, и все корни 
характеристического уравнения различны, то модальной матрицей называется квадратная матрица порядка n, следующего вида
,
153