Рассмотренные примеры позволяют сделать вывод: чем меньше длительность сигнала, тем шире его спектр и наоборот.
6.6. Свойства преобразование Фурье
Для практических приложений важное значение имеет связь между временным преобразованием сигнала и соответствующим ему изменением спектра.
Сдвиг |
колебания во времени. Пусть f1(t) |
существует на интервале |
и |
имеет спектральную плотность |
. При задержке f(t) на |
(форма сохраненяется) получим f2 (t) = f1(t - t0 ), существующую на интервале
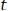
, рис. 6.22.
Спектральная плотность колебания f2 (t) имеет вид
Введём новую переменную интегрирования 
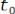, тогда 
, а 
Подставим введённые обозначения в предыдущую формулу
Выражения (6.14) и (6.15) отличаются множителем 
. Следовательно, сдвиг во времени функции 
на величину 
приводит к изменению фазовой характеристики спектра 
на величину 
. Амплитудно-частотная характеристика спектра (т. е. модуль спектральной плотности) от положения сигнала на оси времени не зависит.
Изменение масштаба времени. Пусть сигнал |
f1(t) подвергся сжатию во |
|||||
времени, т. е. |
|
, |
(рис. 6.23), тогда длительность сигнала f2 (t) |
|||
в n раз меньше, чем у исходного сигнала f (t) , и равна |
tи |
. |
||||
|
||||||
|
|
|
1 |
|
n |
|
|
|
|
|
|
||
f1 ( |
) |
f2 |
= f1 ( - 0 ) |
|
|
f2 ( ) |
|
|
f1 ( ) |
||||
|
|
|
|
|||
1 |
1 0 |
2 |
2 |
|
0 |
|
n |
|
и |
|
|
|
|
+ |
|
|
tи |
t |
|
|
|
Рис. 6.22 |
|
|
|
Рис. 6.23 |
|
|
|
111
Спектральная плотность сжатого сигнала определяется выражением
Введём новую переменную интегрирования t = nt , тогда t = nt , а 
= 1n d t
и формулу (6.16) можно преобразовать к виду
Таким образом, при сжатии сигнала в 
раз на временной оси во столько раз расширяется его спектр на оси частот. Модуль спектральной плотности изменяется при этом в n раз.
Очевидно, что при растягивании сигналов во времени(т. е. при n <1) спектр сужается и увеличивается модуль спектральной плотности.
Смещение спектра сигнала. Пусть сигнал f1(t) имеет спектр 
.
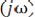Найдём спектр сигнала f2 (t) = f1(t) ×cos w0t .
Умножение сигнала f (t) |
на гармоническое |
колебание |
соответ- |
|
ствует |
расщеплению спектра |
на две части, |
смещённые соответственно |
|
на + |
и – . |
|
|
|
Дифференцирование и интегрирование сигнала.
Преобразование базируется на том, что дифференцирование сигнала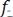 
можно рассматривать как почленное дифференцирование всех гармонических составляющих, входящих в его спектр.
Спектральная плотность производной f2 (t) = df1 равна F2(jω) = jω·F1(jω). dt
Аналогично спектральная плотность интеграла 
равна
112
Сложение сигналов. При сложении сигналов f1(t), f2 (t) ,…, обладающих
спектрами F1( jw) , F2 ( jw) ,…. Суммарному колебанию f (t) = f1(t) + f2 (t) + ...
соответствует спектр 
.
Произведение двух сигналов. Спектр произведения двух функций времени 
и 
определяется выражением
где |
|
|
– спектральная |
функция, являющаяся комплексно- |
|
сопряжённой по отношению к функции |
. |
|
|||
|
Используя выражение (6.16) определим распределение энергии в спектре |
||||
непериодического сигнала. |
|
|
|||
|
Если |
и |
представляют собой один и тот же сигнал |
, |
|
то |
интеграл |
|
|
представляет полную |
энергию |
сигнала через произведение спектральных плотностей. Тогда |
|
||||
Это соотношение устанавливает связь между энергией сигнала и модулем его спектральной плотности. Оно известно под названием равенство Парсеваля.
6.7. Представление сигналов в виде ряда Котельникова
Реальные сигналы имеют конечную длительность и ограниченную полосу частот. Графическое изображение спектра амплитуд даёт наглядное представление о ширине спектра сигнала. В реальных условиях полоса частот сигнала всегда ограничена полосой частот канала передачи или другими условиями.
Для функций с ограниченным спектром В. А. Котельников доказал теорему, лежащую в основе дискретизации непрерывных сигналов и в основе всех видов импульсной модуляции сигналов.
Пусть S(t) – произвольный сигнал, спектральная плотность которого отлична от нуля в полосе
Его можно разложить в обобщённый ряд
¥
Фурье S (t )= å Cnjn.
n=-¥
Выберем в качестве функций 
, функции вида
113
которые образуют ортогональный базис Котельникова. Здесь Dt = |
1 |
– ин- |
|
||
|
2 fm |
|
тервал между двумя точками отсчёта на оси времени. Коэффициенты ряда 
представляют собой мгновенные значения сигналаS(t) в дискретные моменты
времени |
. |
Таким образом |
|
Выражение (6.19) является математической записью теоремы. Из него следует, что в моменты 
значение S(t) определяется только n-ым слагаемым суммы, так как все остальные слагаемые в этот момент равны нулю:
Если наивысшая частота в спектре |
функцииS(t) ограничена величиной |
|||
, то |
функция S(t) полностью |
определяется последовательностью |
||
своих значений |
в моменты, отстоящие друг от друга не более, чем на |
|
|
|
|
||||
секунд.
Непрерывное сообщение можно представить последовательностью - не
прерывных |
дискретных значений |
с интервалами между отсчётами |
|
, |
||
|
||||||
причём |
является обязательным условием (рис. 6.24, а). |
|
|
|||
При передаче сигнала S(t) по каналу связи необходимо взять отсчёты |
||||||
сигнала через равные интервалы |
|
|
и передать по каналу короткие им- |
|||
|
|
|||||
пульсы, площади которых пропорциональны этим отсчётам.
На приёмной стороне эти импульсы пропускаются через фильтр нижних
частот, и сумма откликов фильтра даст |
исходный сигнал, как показано на |
|
рис. 6.24 б. |
|
|
Таким образом, каждое слагаемое ряда(6.19) представляет отклик иде- |
||
ального фильтра нижних частот с частотой среза |
на весьма короткий им- |
|
пульс, приходящий в момент времени |
и имеющий площадь, равную |
|
мгновенному значению функции S(t) в тот же момент.
114
S(t)
а
t
S(0)
t
б
S(0)
S (0) × sin wmt wmt
S (Dt) × sin wm (t - Dt) wm (t - Dt)
S (2Dt) × sin wm (t - 2Dt) wm (t - 2Dt)
S
Рис. 6.24
115