где – собственные значения матрицы A (или корни характеристического уравнения).

Любая квадратная матрица A, все собственные значения которой различны, преобразуется в диагональную матрицу , элементами которой являются эти собственные значения следующим образом

7.14. Каноническая форма уравнений состояния

Будем считать, что нормальная форма известна

(7.21)

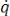Введем новую переменную , которая связана с следующим образом: и подставим в (7.21), тогда

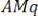
Умножим первое уравнение слева на , тогда С учетом (7.21) получим

видом матриц и .

Перейдем к скалярной форме записи в виде системы дифференциальных уравнений первого порядка

154

Схема моделирования, соответствующая системе (7.23) приведена на рис. 7.17. Для нее характерно параллельное соединение интеграторов.

Преимущество канонической формы в том, что каждое дифференциальное уравнение зависит только от одной переменной и решается просто. Выход системы y складывается из суммы решений отдельных уравнений.

u

Рис. 7.17. Схема моделирования канонической формы уравнений состояния

Пример 7.6. Передаточная функция системы имеет вид

Записать каноническую форму уравнений состояния, изобразить схему моделирования, определить реакцию системы на сигнал. Вначале найдем матрицы , соответствующие нормальной форме уравнений состояния

155

Дифференциальное уравнение, описывающее исходную систему имеет

вид

тогда

, .

Каноническая форма уравнений состояния имеет вид

,

Элементами диагональной матрицы являются характеристические числа матрицы , которые определяются решением уравнения

Запишем соответствующее уравнения

156

Переходя к скалярной форме записи, получим

Соответствующая схема моделирования приведена на рис. 7.18.

выглядеть следующим образом

тогда решение уравнения имеет вид

а решение уравнения имеет вид

157