7.16. Математическое описание дискретных систем и их элементов

Дискретные системы автоматического управления включают в себя цифровые и импульсные системы.

В цифровых системах осуществляется квантование сигналов по уровню и по времени. В импульсных системах осуществляется только квантование по времени, для таких систем характерна амплитудно-импульсная модуляция сигналов.

Понятие о решетчатых функциях. Процессы, происходящие в импульсных системах, описываются функциями дискретного аргумента, так называемыми решетчатыми функциями. Решетчатые функции образуются из соответствующих непрерывных функций при дискретизации их в равноотстоящие мо-

.

Оператор для дискретных функций является аналогом дифференциаль-

ного оператора для непрерывных функций.

162

Разность второго порядка определяется как

Разность третьего порядка равна

Соответственно разность произвольного порядка можно представить следующим образом

Системы, в которых взаимосвязь между входом и выходом определяется только в равностоящие моменты времени описываются разностными уравнениями.

Уравнение в конечных разностях имеет вид

Если в (7.24) выразить разности через значения решетчатой функции, то разностное уравнение будет иметь вид

(7.25)

Выражение (7.24) является более близким аналогом дифференциального уравнения, однако выражение (7.25) легче использовать и такая форма разностного уравнения более распространена.

Z-преобразование и его свойства. Подобно тому, как применение преобразования Лапласа к дифференциальным уравнениям дает возможность -пе рейти к алгебраическим уравнениям и получить удобную инженерную методику анализа, так и для дискретных систем был разработан ряд специальных преобразований. Наибольшее распространение получили дискретное преобразование Лапласа и Z-преобразование, которое является дискретным аналогом преобразования Лапласа.

аргумента , определяемая следующим выражением

163

для .

Если , где – оператор Лапласа, то -преобразование после перехода к переменной представляет собой обычное преобразование Лапласа, примененное к последовательности -функций, площадь каждой из которых определяется соответствующим значением . Это и есть дискретное преобразование Лапласа

Z-преобразование для смещенной решетчатой функции называется модифицированным

Рассмотрим основные свойства -преобразования 1. Теорема смещения. Сдвиг функции-оригинала вправо по оси времени

на интервалов дискретности соответствует умножению изображения на

.

Если сдвиг оригинала по оси времени происходит влево на целое число интервалов дискретности

Если для , то второй член в правой части уравнения обращается в нуль

.

2.Линейность. -преобразование алгебраической суммы функций равно алгебраической сумме их -преобразований и постоянный множитель можно выносить за знак -преобразования.

3.Теорема о предельных значениях

164

4.Изображение конечных разностей. Если ,

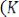
то .

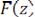
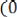
5.Теорема свертки

Передаточная функция дискретной системы . Передаточная функция разомкнутой дискретной системы с одним входом и одним выходом равна отношению -преобразования выходного сигнала кZ-преоб- разованию входного сигнала при нулевых начальных условиях.

Передаточная функция может быть записана непосредственно по разностному уравнению с учетом теоремы смещения. Например, если разностное уравнение имеет вид

, то, переходя к Z-преобразованию, получим

Тогда

Знаменатель передаточной функции, приравненный к нулю, называется характеристическим уравнением разомкнутой импульсной системы

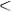
Для устойчивости дискретных систем необходимо и достаточно, чтобы корни характеристического уравнения замкнутой системы были расположены внутри единичного радиуса с центром в начале координат, . Так как , то левая часть – плоскости для непрерывных систем, отображается на плоскости внутрь единичного круга (в полярных координатах ).

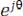Обратное Z-преобразование. Для нахождения дискретной функции(оригинала) по ее заданному Z-преобразованию используется обратное Z-преобразование. Обратное Z-преобразование может быть получено двумя способами:

-разложение заданного преобразования в ряд по степеням ;

-с помощью интегральных вычетов.

Из определения Z-преобразования ясно, что коэффициент при разложения будет равен значению искомой функции

165