6.4. Комплексная форма ряда Фурье

Спектральное разложение периодического сигнала f (t) можно выполнить, используя систему базисных функций, состоящую из экспонент с мнимыми показателями … , , 1, , … .

Функции этой системы периодичны с периодомT и ортонормированны

¥

f (t) = å A&ne jnwt ,

n=-¥

где комплексная амплитуда

Спектр сигнала содержит компоненты на отрицательной полуоси частот, причём . Слагаемые с положительными и отрицательными частотами объединяются в пары

=

поэтому при переходе к тригонометрической форме ряда записывается f (t) следующим образом

Итак, отрицательная частота – понятие не физическое, а математическое, вытекающее из способа представления на комплексной плоскости.

Для рассмотренного ранее примера 6.1.

105

Вычислим значения An для различных n

Результат получится такой же, как в примере 6.1.

6.5. Гармонический анализ непериодических сигналов. Преобразование Фурье

Пусть f (t) − одиночный импульсный сигнал конечной длительности (рис. 6.17). Дополним его мысленно такими же сигналами, периодически следующими через время T. Тогда периодический сигнал может быть представлен

в виде комплексного ряда Фурье

Подставим (6.8) в (6.9)

106

Для того, чтобы вернуться к одиночному импульсному сигналу, устремим

Tк бесконечности. Тогда

1)частоты соседних гармоник nw и (n +1)w окажутся настолько близки-

ми, что дискретную переменную nw можно заменить текущей частотой w,

2)значение ω можно заменить на dw (так как w ® 0 ),

3)амплитудные коэффициенты станут неограниченно малыми из-за наличия в знаменателе.

Найдём предельный вид формулы при 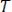, заменив операцию суммирования интегрированием.

t2

Внутренний интеграл F ( jw) = ò f (t)e- jwt dt – называется спектральной

t1

плотностью функции . называют также частотной характеристикой функции , так как она представляет собой непрерывный спектр функции

. В общем случае, когда пределы и не уточнены, спектральная плотность записывается в форме

После подстановки (6.12) в (6.11) получим

Выражения (6.12) и (6.13) называются соответственно прямым и обратным преобразованием Фурье, которые лежат в основе гармонического(частотного) анализа непериодических сигналов. Эти выражения ставят во вза-

Модуль и аргумент спектральной плотности определяются выражениями

107

Первое из выражений можно рассматривать как амплитудно-частотную, а второе – как фазочастотную характеристику сплошного спектра непериодического сигнала f (t) .

Если спектральная плотность сигнала рассматривается отличной от нуля в пределах некоторой полосы частот конечной протяжённости, то говорят о сигнале с ограниченным спектром.

Если F (w) имеет вид, приведённый на рис. 6.18 а, то под шириной спектра W понимают частотный интервал, в пределах которого модуль спектральной плотности не меньше уровня 0,1Fmax.

Если F (w) имеет вид, приведённый на рис. 6.18, б, то ширина спектра

может быть оценена границей первого лепестка W = 2p . tи

Рассмотрим сигнал со спектральной плотностью, постоянной в пределах

[-W, W], (рис. 6.19, а).

F(w) = ìíF0 , wÎ[-W, W],

î0, при других w.

При переходе во временную область

Соответствующий сигнал показан на рис. 6.19, б. Такой сигнал называется идеальным низкочастотным, так как он имеет простейший спектр. Его можно рассматривать как выходную реакцию фильтра нижних частот, на входе которого действует d–импульс, т. е. сигнал с равномерной по частоте спектральной плотностью.

Рис. 6.18

108

Рис. 6.19

Рассмотрим примеры определения спектров непериодических сигналов. Пример 6.5. Импульс прямоугольной формы описывается выражением:

Найти спектральную плотность сигнала. В соответствии с (6.12) определим выражение для спектральной плотности

Здесь использованы формулы Эйлера

Спектр сигнала приведён на рис. 6. 20.

F (w)

Сτ

ω

Рис. 6.20

109

длительность τ, тем меньше расстояние между нулями функции F (w) , что равносильно сужению спектра.

Пример 6.6. Найти спектр сигнала в виде дельта функции f (t) = d(t). Выражение для спектральной плотности такого сигнала имеет вид:

Здесь использовано фильтрующее свойство -функции:

F(ω)

1

функции не выполняется условие абсолютной интегрируемостиò f (t)dt < ¥, то

-¥

функцию домножают на коэффициент , где и находят преобразование Фурье от произведения , которое удовлетворяет условию абсолютной интегрируемости. Далее переходят к пределу при С стремящемся к нулю.

Устремляя С к нулю, в пределе получаем следующее выражение для спектральной плотности единичного скачка.

110