Случайными называют сигналы, значения которых заранее неизвестны и могут быть предсказаны лишь с некоторой вероятностью, меньшей 1. Для характеристик и анализа случайных процессов применяется статистический подход, случайные сигналы характеризуются такими параметрами, как математическое ожидание, дисперсия и т. п.

6.2. Спектральное представление сигналов. Разложение произвольного сигнала по заданной системе функций

k =1

т. е. любой сигнал может рассматриваться как совокупность элементарных сиг-

В качестве базисных выбирают такие функцииjk (t) , которые на заданном интервале [a, b] обладают свойством ортогональности, т. е.

b

òjmjk (t)dt = 0 при m ¹ k.

a

Выбор jk (t) из класса ортогональных даёт наилучшее приближение к ряду: среднеквадратичная ошибка (СКО) аппроксимации s на [a, b] минимальна при фиксированном числе N слагаемых ряда (6.1).

-¥

Именно такая энергия выделяется в резисторе с сопротивлением1 Ом, если на его зажимах существует напряжение f (t).

Два сигнала u(t) и v(t) ортогональны, если их скалярное произведение, а, значит, и взаимная энергия равны нулю

¥

(u,v) = ò u(t)v(t)dt = 0.

-¥

Разнесённые во времени сигналы ортогональны.

Выбор ортогональной системы функций зависит от постановки задачи, при этом можно выделить два направления:

1)точное разложение на простейшие ортогональные функции;

2)аппроксимация сигналов минимальным числом членов ряда при заданной допустимой погрешности.

В первом случае применяют систему основных тригонометрических функций – sin и cos, так как гармоническое колебание является единственной функцией времени, которая сохраняет свою форму при прохождении через любую линейную цепь с постоянными параметрами, изменяются только амплитуда и фаза сигнала. Кроме того при разложении сложного сигнала поsin и cos можно использовать для анализа символический метод (преобразование Лапласа).

Во втором случае применяются разнообразные ортогональные системы функций: полиномы Чебышева, Эрмита, Лагерра, Лежандра и др.

Если система функций jk выбрана, то сигнал будет определяться сово-

купностью коэффициентов Ck.

Умножим обе части выражения (6.1) на jn (t) и проинтегрируем его в пределах от a до b.

a

96

С учётом (6.3) выразим Cn из (6.2), при этом

Ряд, в котором коэффициенты определяются в соответствии с выражением (6.4), называется обобщённым рядом Фурье.

6.3. Гармонический анализ периодических сигналов

Пусть задан периодический сигнал f (t) с периодом T. Выберем в качестве базисных систему ортогональных тригонометрических функций1; cos w t; sin w t; cos 2w t; sin 2w t;...; cos nw t;sin nw t. Интервал ортогональности совпадает

с периодом функции f (t) и равен T = 2wp .

При этом ряд (6.1) с коэффициентами (6.4) запишется следующим образом:

T

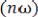вой гармоники. Говорят, что осуществлено спектральное разложение этого сигнала. Отдельные гармонические компоненты сигнала образуют его спектр. Совокупность величин и называются соответственно амплитудным и фазовым частотными спектрами периодической функции f (t).

Спектры являются функциями, зависящими от номера гармоникиn, как независимой переменной. Графически спектры удобно изображать в виде -от резков длины и , проведённых перпендикулярно к оси w .

97

Число n может принимать как положительные, так и отрицательные значения, поэтому графики спектров и имеют смысл и при положительных и при отрицательных частотах nw . Следует отметить, что амплитудно-частотный спектр является чётно-симметричной, а фазочастотный спектр– нечётносимметричной функцией частоты nw . Поэтому при построении спектров достаточно отображать лишь их половину при nw > 0.

Пример 6.1. Найти и построить спектры прямоугольного сигнала, называемого меандром (рис. 6.8), который широко применяется в измерительной технике.

f (t) C

-C 0

При чётных значениях n и n = 0 cosnπ = 1 и выражение в скобках обращается в нуль, так что нулевой составляющей и чётных гармоник данное выражение не содержит.

Вычислим коэффициенты bn:

98

Представим функцию f (t) в виде суммы гармонических составляющих

С увеличением числа суммируемых гармоник сумма ряда приближается к функции f (t).

Спектр коэффициентов тригонометрического ряда рассматриваемого сигнала определяется выражением и приведен на рис. 6.9, а. Фазоча-

ставлен на рис. 6.9, б. Для всех гармонических составляющих значения началь-

ных фаз .

Рис. 6.9

Спектр периодической функции называется линейчатым или дискретным, так как состоит из отдельных линий, соответствующих дискретным частотам.

Средняя мощность сигнала, рассматриваемого на всей оси времени, совпадает со средней мощностью сигнала за период T, которая вычисляется по формуле

Вычислим среднюю мощность, используя разложение f (t) в ряд. Учитывая, что и , получим

99

Представим f (t) в виде суммы гармонических составляющих

Амплитудно-частотный спектр представлен на рис. 6.13. Здесь учтено, что . Начальные фазы всех гармоник будут равны нулю, так как

5

Рис. 6.13

102

Пример 6.4. Построить спектральные характеристики сигнала, представляющего собой последовательность униполярных прямоугольных импульсов

(рис. 6.14).

Cf (t)

T

Рис. 6.14

Так как f (t) – чётная функция, все коэффициенты . Найдём коэффициенты :

Представим f (t) в виде ряда

Умножим и разделим выражение под знаком суммы на nwt , тогда

2

График этой функции представлен на рис. 6.15. sin x = 0 при x = kp, а

при x ® 0 sin x » x, тогда sin x = 1. Эта функция является огибающей спектра x

коэффициентов ряда.

103

Рис. 6.15

Амплитудно-частотный спектр 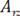представлен на рис. 6.16. Начальные

фазы всех гармонических составляющих равны нулю, так как arctg bn = 0 . an

ω

w1 w3

Рис. 6.16

Величина N = Tt называется скважностью импульсной последовательно-

сти. Чем больше длительность импульса τ, тем уже спектр сигнала, и наоборот. чем меньше длительность сигнала, тем шире спектр.

104