7.8. Построение логарифмических частотных характеристик разомкнутых одноконтурных систем

Предварительно передаточную функцию системы представляют в виде произведения передаточных функций отдельных звеньев. Тогда ЛЧХ системы формируется суммированием ЛЧХ отдельных звеньев.

Рассмотрим систему с передаточной функцией

которую можно рассматривать как последовательное соединение – интегрирующих звеньев, – форсирующих звеньев и – апериодических звеньев. Если

есть идеальные дифференцирующие звенья, то будет отрицательным числом.

При переходе к логарифмическому масштабу логарифмические частотные характеристики отдельных звеньев складываются, на этом основано при-

вило построения ЛАЧХ разомкнутой системы.

Последовательность действий следующая:

1. Определить все сопрягающие частоты и отметить их на оси

абсцисс.

2. Первая линия в области низких частот проводится через точку с координатами с наклоном . Линия проводится до первой сопрягающей частоты (минимальная на оси частот).

3. Продолжить построение, изменяя наклон после каждой из сопрягающих частот в зависимости от того, какому звену эта частота принадлежит. Каждое апериодическое звено изменяет наклон на, а каждое форсирующее на .

4. Выражение для фазочастотной характеристики имеет вид:

Оно определяется как сумма значений ФЧХ каждого из элементов системы на фиксированной частоте.

Пример 7.3. Построить ЛАЧХ и ЛФЧХ для системы с передаточной функцией

143

определяется наличием идеального интегрирующего звена и проведен через точку с координатами На частоте наклон ЛАЧХ изменяется до (-2), так как является сопрягающей частотой для апериодического звена. На частоте наклон ЛАЧХ становится равным (-1), так как является сопрягающей частотой принадлежащей форсирующему звену. ЛФЧХ получена в результате сложения характеристик отдельных звеньев: интегрирующего, апериодического и форсирующего.

Рис. 7.12. Пример построения ЛЧХ разомкнутой системы.

7.9. Математические модели элементов в параметрах пространства состояний

Для отдельного элемента или системы кроме входных и выходных переменных можно выделить некоторую совокупность промежуточных переменных, которые связаны с внутренней структурой устройства, обозначаются и называются переменными состояния.

144

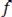
Описание при помощи переменных состояния позволяет представить многие физические системы совокупностями дифференциальных уравнений первого порядка вида которые называются дифферен-

циальными уравнениями состояния, и совокупностями алгебраических

подразумевается, что система имеет несколько входов и несколько выходов. В дальнейшем рассматриваются линейные стационарные устройства и системы с одним входом и одним выходом. Количество переменных состояния n определяется порядком системы. Все состояния системы образуют вектор состояний, множество которых образует пространство состояний.

Математическая модель элементов, описываемых уравнениями первого порядка, имеет вид:

(7.8)

где , , и – постоянные числа.

Уравнения (7.8) удобно представить в виде структурной схемы или схемы моделирования. Построение схемы (рис. 7.13) начинается с изображения интегратора, который обозначается соответствующим знаком.

Рис. 7.13. Схема моделирования элемента первого порядка

Переменная состояния 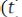ассоциируется с выходом интегратора, тогда сигнал на входе интегратора можно обозначить через. Для формирования сигнала 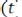нужно проинтегрировать его производную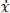 и замкнуть контур из условия удовлетворения дифференциальному уравнению Контур с блоком называется контуром обратной связи. Выходной сигнал

145

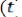является выходом сумматора, на который подаются сигналы и . Элементы схемы, внутри которых записаны коэффициенты и моделируют блоки преобразования сигналов с соответствующими коэффициентами усиления.

7.10. Решение уравнений состояния первого порядка

Вначале найдем решение уравнений состояния первого порядка с постоянными коэффициентами

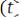Решение первого уравнения складывается из общего решения однородного уравнения (с нулевым входным воздействием, т. е. и частного решения неоднородного уравнения .

Решение однородного уравнения найдем методом разделения переменных

уравнения, оно не зависит от входного воздействия и определяется только параметрами системы. Так как характеризует естественное поведение системы при отсутствии внешних сигналов(возмущений), его называют свободным или невынужденным движением.

Частное решение можно найти методомвариации постоянной. Для

тогда

где – частное решение, оно зависит как от параметров системы, так и от входного воздействия, его называют вынужденным движением.

146