Ломоносова Сборник задач по квантовой електродинамике 2010

145. Рассматриваемый процесс непосредственно измеряется на ускорителях со встречными e+e−-пучками. В e+e−-столкновениях учет обмена слабым нейтральным бозоном Z0 (наряду с однофотонным обменом) становится существенным при высоких энергиях пары E. Процесс описывается двумя диаграммами Фейнмана, одна из которых – это диаграмма рис. 13 с обменом фотоном, а другая – такая же, но с обменом Z0-бозоном.

Исходя из формы лагранжиана взаимодействия Z0 c (e+e−) и (µ+µ−), можно определить вершины Z0ee (Z0µµ). При взаимодействии с левыми биспинорами вершина имеет вид:

1

−ıg¯(−2 + ξ)γµ,

При взаимодействии с правыми биспинорами вершина выглядит как:

−ıgξγ¯ µ.

Отсюда по правилам Фейнмана инвариантная амплитуда, отвечающая сумме диаграмм однофотонного обмена и обмена Z0, запишется в виде (в обозначениях задачи 117):

Здесь k2 = (p1 + p2)2 = s. Очевидно, при низких энергиях, когда s MZ2 , пропагатор второй части амплитуды становится мал

12 , и процессом обмена Z0 можно пренебречь.

MZ

181

Диаграммы, в которых квадрат 4-импульса промежуточной частицы равен инвариантной переменной s, называются s-каналь- ными диаграммами.

Далее удобно выразить амплитуду только через левые и правые биспиноры. Имея в виду, что

(то же для v(p)), а также, что u¯LγµuR = 0 (и с заменой u на v), найдем для электромагнитной амплитуды однофотонного обмена:

e2

Tγ = k2 [¯v(p2)γµu(p1)][¯u(p3)γµv(p4)] =

e2

= k2 [¯vL(p2)γµuL(p1) + v¯R(p2)γµuR(p1)]×

× [¯uL(p3)γµvL(p4) + u¯R(p3)γµvR(p4)].

Поскольку фотон зарядово нечетен, то пара µ+µ− в случае однофотонного обмена рождается с зарядовой четностью C = −1 (вершина γee содержит только векторное взаимодействие γµ). Вершина же взаимодействия с Z0 содержит как векторное, так и аксиальное взаимодействие γ5γµ, которые при операции зарядового сопряжения преобразуются по-разному (см. задачу 84). Поэтому рождению µ+µ− отвечает суперпозиция состояний с C = 1 и C = −1. Интерференция состояний с противоположной зарядовой четностью должна приводить к зарядовой асимметрии в угловом распределении µ+ и µ−, что будет показано в задаче 147.

146. Покажем, что в пренебрежение массой электрона (и то же

для мюона) продольная часть пропагатора Z0-бозона kµkν

k2−MZ2 +ı

вклада не дает. Для этого рассмотрим амплитуду T процесса, полученную в предыдущей задаче. Внесем kµ в последний множитель в квадратных скобках, представляющий электронную линию. Выражение в квадратных скобках обратится в нуль. Действительно, рассмотрим подробнее первое слагаемое в квадратных скобках:

182

(и то же для второго слагаемого). Нулевой результат получается потому, что pˆ антикоммутирует с матрицей γ5, а уравнение Дирака для безмассовых частиц дает: pˆ1u(p1) = 0, v¯(p2)pˆ2 = 0.

!

× (¯u3Lγµv4L)(¯v2Rγµu1R) + (¯u3Rγµv4R)(¯v2Lγµu1L) .

Если в амплитуде положить r = 0, то останется вклад чисто электромагнитного взаимодействия.

При возведении амплитуды в квадрат и усреднении по начальным и суммировании по конечным поляризационным состояниям четыре слагаемых, входящих в амплитуду, не интерферируют. Физически это обстоятельство объясняется различными спиральностями начальных (конечных) частиц. С другой стороны, к тому же результату приводит вычисление следов – следы от произведения правых и левых скобок обращаются в нуль. Это показано ниже в задаче 147.

Выпишем для данного процесса инвариантные переменные, пренебрегая массами электрона и мюона:

s = (p1 + p2)2 = (p3 + p4)2 = k2,

s

t = (p1 − p3)2 = (p2 − p4)2 = −2(p1p3) = −2 (1 − cos θ),

183

s

u = (p1 − p4)2 = (p2 − p − 3)2 = −2(p1p4) = −2 (1 + cos θ),

где θ – угол рассеяния, угол между e− и µ−.

147. Вычислим квадрат модуля амплитуды e+e− → µ+µ−, полученной в задаче 146, и по стандартным правилам (см. задачу 114) усредним по начальным и просуммируем по конечным поляризационным состояниям фермионов. Для примера вычислим мюонный след, возникающий при усреднении по поляризациям квадрата модуля первого слагаемого (содержащего левые биспи-

= 2[p3µp4ν + p3ν p4µ − (p3p4)gµν + ı αµβν p3αp4β ]

Усреднение по электрон-позитронным поляризациям (с левыми биспинорами) приводит к тому же результату с заменой p3 на p1 и p4 на p2. В случае усреднения, содержащего правые фермионные состояния, просто меняется знак перед αµβν .

Покажем далее, что при усреднении правые мюонные (электронные) формы не интерферируют с левыми и наоборот.

Выражение обращается в нуль, так как (1 + γ5)(1 − γ5) = 0 и

γµγ5 + γ5γµ = 0.

Дифференциальное сечение после вычисления следов и подстановки инвариантных переменных (задача 146) приобретает вид:

dσ = α2 [Au2 + Bt2] = dΩ 2s3

=α2 [(A + B)(1 + cos2 θ) + (A − B)2 cos θ]. 8s

184

Здесь

При r = 0 константы A = B = 1, и сечение переходит в результат для электромагнитного взаимодействия задачи 117 в ультрарелятивистском приближении, причем асимметрия вылета мюонов не наблюдается – дифференциальное сечение в однофотонном приближении не меняется при замене θ → (π − θ), т.е. при замене µ− → µ+. При r = 0 угловое распределение отрицательных мюонов содержит слагаемое, пропорциональное cos θ, которое меняет знак при вышеупомянутой замене частицы на античастицу и приводит к асимметрии их вылета. Очевидно, что за появление асимметрии, как и указано в задаче 145, несет ответственность слабый нейтральный ток – обмен Z0-бозоном. Измеренная на опыте в области высоких энергий асимметрия вылета вперед-назад составляет порядка 10%.

Экспериментальное значение ξ = sin2 ϑW 0.23. Константа g¯ определяется параметрами электрослабой модели и электриче-

ским зарядом e: g¯ = e .

sin ϑW cos ϑW

148. Особый интерес представляет рассеяние, когда в s-канале реакции (например, e+e−-аннигиляции) происходит обмен нестабильной частицей R с массой MR и полной распадной шириной Γ. При s → MR2 амплитуда процесса становится близка к полюсу пропагатора нестабильной частицы (s − MR2 )−1 (см. задачу 145), и рассеяние становится резонансным.

Если τ – время жизни нестабильной частицы, то вероятность застать ее в состоянии с волновой функцией ψ(t) (пусть при t < 0 ψ ≡ 0) определяется квантово-механическим соотношением:

|ψ(t)|2 = |ψ(0)|2 e−τt .

185

Поскольку для стационарных состояний ψ(t) = ψ(0)e−ıEt, то заданному временному закону изменения вероятности удовлетворяет комплексное значение энергии E = E0 − ıΓ/2, где Γ – ширина уровня. Время жизни распадающегося состояния связано с его шириной формулой τ = Γ1 (или в обычных единицах τ = Γ ). Это утверждение полностью согласуется с соотношением неопределенностей E t : когда состояние имеет конечное время

жизни τ , неопределенность (размазанность) в его энергии составляет E ≈ τ .

Чтобы прояснить смысл появления у E мнимой части, перейдем к энергетическому представлению:

|˜( )|2

ψE определяет вероятность частице иметь энергию E:

Распадающееся состояние обладает не одним значением энергии, а некоторой областью, задаваемой его шириной Γ, с центральным значением E = E0. Полученное соотношение содержит резонансный знаменатель, определяемый в нерелятивистской квантовой механике формулой Брейта – Вигнера.

Модифицируем в релятивистскую область нерелятивистский

(ширина нестабильной частицы определяется модами ее распада). Для этого домножим его числитель и знаменатель на (E + ER), где ER – энергия резонансной частицы. Теперь E0 ≡ ER, s = E2,

sR = ER2 = MR2 . Вблизи резонанса E ≈ ER и E + ER ≈ 2MR. В резонансном приближении получаем:

186

Иначе говоря, для получения пропагатора нестабильной частицы с полной шириной распада Γ и при условии, что Γ MR, следует сделать замену в знаменателе

1

MR → MR − 2 ıΓ.

149. В e+e−-столкновениях на ускорителях со встречными пучками, если s = 4E02 ≈ MZ2 , имеет место резонансное рождение Z0 (E0 – энергия каждого пучка). Образовавшийся Z0-бозон нестабилен – он быстро распадается по нейтринному, лептонному или

его распада Γ ≈ 2, 5 ГэВ, а MZ ≈ 90 ГэВ. Следовательно, условие Γ MZ выполняется, поэтому в формуле задачи 145 для амплитуды процесса можно с хорошей точностью заменить знаменатель пропагатора резонансным знаменателем, т.е. (s−MZ2 ) → (s − MZ2 + ıMZ Γ). В сечении процесса, таким образом, возникает резонансный множитель

1

R = (s − MZ2 )2 + MZ2 Γ2 .

В задаче 147 было вычислено дифференциальное сечение процесса e+e− → µ+µ− с учетом однофотонного обмена и обмена Z0. Выделив из него только ту часть сечения, которая ответственна за Z0-обмен ( r2) и интегрируя по телесному углу dΩ, получим полное сечение процесса в резонансном приближении:

В области s MZ2 подавляющий вклад в сечение вносят слабые взаимодействия. Сечение, обусловленное рождением Z0, обладает резким и узким пиком при √s ≈ MZ . Высота пика в 160 раз превышает электромагнитное сечение, а его ширина Γ. Однако в области малых энергий сечение, обусловленное слабым взаимодействием, становится очень малым по сравнению с электромагнитным.

187

Таким образом, существование Z0 может быть обнаружено как наличие узкого резонансного пика в сечении столкновения электронов и позитронов. Предсказанный резонанс был не только найден на ускорителе LEP, но и с высокой точностью были измерены характеристики Z0.

Если вычислить с привлечением электрослабой модели ширины распадов Γ(Z0 → e+e−) и Γ(Z0 → µ+µ−), то резонансное сечение может быть представлено в весьма общей форме:

В заключение заметим, что в пределе Γ M резонансный пик становится чрезвычайно острым, напоминающим δ-функцию, и имеет место следующее приближенное соотношение:

7.2. Некоторые вопросы высших порядков теории возмущений в КЭД

150. Проанализируем степень расходимости диаграмм КЭД. Если число импульсов в числителе меньше числа импульсов в знаменателе, то результат для данной диаграммы окажется сходящимся, в противном случае – расходящимся. Определим «размерность» стоящих в амплитуде интегралов как разность полного числа импульсов в числителе и полного числа импульсов в знаменателе и обозначим ее через D. Тогда достаточным условием сходимости будет D < 0, а расходимости – D ≥ 0.

Пусть в заданной диаграмме Fe – число внешних фермионных и антифермионных линий, Be – число внешних фотонных линий, Fi – число внутренних фермионных и антифермионных линий, Bi

188

– число внутренних фотонных линий и n – число вершин. Структура вершины КЭД (−ıeγµ) не содержит импульсов, внешние линии также не содержат импульсов и не влияют на расходимость. На расходимость влияют следующие факторы:

1. Каждая внутренняя фермионная (антифермионная) и фо-

тонная линии дают четыре 4-импульса в числитель (фактор d4p):

4(Fi + Bi).

2. В каждой вершине стоит фактор δ(4) ( k pk). Это эквивалентно четырем 4-импульсам в знаменателе. Одна из δ(4)-функций выражает закон сохранения процесса в целом и не приводит к

уменьшению размерности интеграла. Таким образом, вершины дают вклад: −4(n − 1).

3. Каждая внутренняя фермионная (антифермионная) линия

содержит фактор pˆ±m p−1; Fi линий дают вклад: −Fi.

p2−m2

4. Каждая внутренняя фотонная линия содержит фактор k12 ; Bi линий дают вклад: −2Bi.

Следовательно,

D = 4(Bi + Fi) − Fi − 2Bi − 4(n − 1) = 2Bi + 3Fi − 4(n − 1).

Выразим эту величину через число внешних линий диаграммы. В КЭД в каждой вершине сходятся две фермионные (антифермионные) линии и одна фотонная линия. Число концов фермионных линий равно удвоенному числу вершин, причем внутренние фермионные (антифермионные) линии дают две вершины, а внешние

– одну: 2n = Fe + 2Fi. Число концов фотонных линий равно числу вершин: n = Be + Bi. Отсюда

D = 3Fi+2Bi−4(n−1) = 3(n−F2e )+(n−Be)−4(n−1) = 4−32 Fe−Be.

Таким образом, степень расходимости диаграмм КЭД не зависит от числа вершин, т.е. от порядка теории возмущений, а определяется только внешними линиями диаграммы – степень расходимости не увеличивается с ростом порядка теории возмущений. Этот факт является одним из условий перенормируемости теории. В действительности КЭД содержит расходимости не выше логарифмической.

189

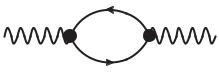
151. Фейнмановская диаграмма для поляризационного оператора во втором порядке теории возмущений представлена на рис. 27.

−(k − p)

p

Рис. 27

Поляризационный оператор Πµν является тензором, зависящим от индексов γ-матриц µ и ν, стоящих в вершинах диаграммы, причем очевидно, что в силу симметрии диаграммы тензор должен быть симметричным. Можно записать самое общее выражение для тензора Πµν , используя симметричный метрический тензор gµν и 4-импульс фотона kµ. Общий вид тензора Πµν имеет вид:

Πµν = Π1(k2)k2gµν + Π2(k2)kµkν .

Мы построили симметричный тензор Πµν . Здесь Π1,2(k2) – скалярные функции переменной k2. Требование калибровочной инвариантности kν Πµν = 0 (см., например, задачу 128) приводит к условию:

Πµν kν = (Π1(k2) + Π2(k2))kµ = 0.

Отсюда в силу произвольности kµ следует, что Π2 = −Π1 ≡ Π0(k2). Окончательный вид тензора Πµν :

Πµν = Π0(k2)(kµkν − k2gµν ).

Первое слагаемое в Πµν называется продольной частью поляризационного оператора и, как правило, вклада в процессы не дает, второе слагаемое называется его поперечной частью.

190