Ломоносова Сборник задач по квантовой електродинамике 2010

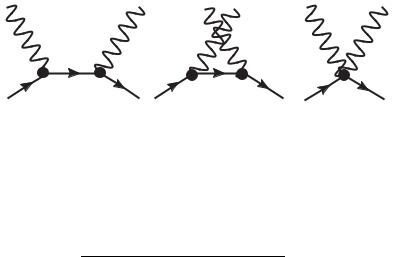
поглощенного фотонов. Множитель 2 связан с тем обстоятельством, что любой из двух потенциалов Aµ(x) может соответствовать как поглощению, так и испусканию фотона.

106. Диаграммы Фейнмана для процесса комптоновского рассеяния на заряженной частице с нулевым спином представлены на рис. 8 (см. также задачу 89).

Рис. 8

Используя известные правила Фейнмана и правила, полученные в задачах 104 и 105, выписываем амплитуду рассматриваемого процесса:

ε(2σ) → ε(2σ) + bk2, где a и b – произвольные величины. Отметим, что p + p2 = 2p2 + k2, p + p1 = 2p1 + k1, p + p2 = 2p2 − k1,

131

p +p1 = 2p1−k2. Учтем, что (k1 ε1(λ)) = 0 и (k2ε(2σ) ) = 0 в силу условия Лоренца. Калибровочная инвариантность позволяет в опре-

деленной системе отсчета выбрать две независимые поляризации реальных фотонов трехмерно поперечными. Сделаем это в лабораторной системе отсчета, где p1 = 0. Тогда 4-векторы ε(1λ) и ε(2σ)

удовлетворяют дополнительным условиям: (p1ε(1λ)) = (p1ε(2σ) ) = 0. В силу этих условий и условий Лоренца первые два слагаемых в Sf i обращаются в нуль. Отличен от нуля только вклад слагаемого, отвечающего на рисунке случаю в. Таким образом, элемент S-матрицы данного процесса имеет вид:

а инвариантная амплитуда: Tf i = 2e2(ε(1λ) · ε(2σ) ). Дифференциальное сечение процесса вычисляется по стандартной формуле:

Здесь e2 = 4πα (α = 1371 ); dΩ2 – элемент телесного угла, в котором регистрируется γ-квант, рассеянный в лабораторной системе;

Энергия ω2 вычисляется из уравнения

E2=m + ω1 − ω2 = ω12 +ω22 − 2ω1ω2 cos θ2 + m2

132

Подставляя полученные результаты в выражение для dσf i, получим:

Отметим, что фактор (ε(1λ) ·ε(2σ) ) = −(ε(1λ) ·ε(2σ) ), так как поляризации фотонов трехмерно поперечны. Суммирование по двум

поперечным поляризациям вторичного фотона и усреднение по поляризациям первичного фотона проводится по формулам:

λ,σ

В результате находим угловое распределение рассеянных фотонов:

В пределе мягких фотонов (ω1 m) получаем классическую формулу для сечения эффекта Комптона:

133

Это классическая формула Томсона, где r0 = mα – классический

2

радиус электрона (в обычных единицах r0 = mce 2 ).

107.Решение аналогично решению задачи 102.

108.Уравнение для функции Грина фермиона с зарядом e,

взаимодействующего с электромагнитным полем, которое описывается 4-потенциалом Aµ(x), имеет следующий вид:

Уравнение для функции Грина можно представить в эквива-

где S0(x2 − x1) – функция Грина свободного фермиона. Подставляя это соотношение в верхнее уравнение для функции Грина и учитывая, что свободная функция Грина удовлетворяет уравне-

нию (pˆ − m)S (x − x ) = ıδ(4) (x − x ), убеждаемся в эквива-

2 0 2 1 2 1

лентности дифференциального и интегрального уравнений для S. Приближение однократного взаимодействия получается, если в интегральном уравнении для S под знаком интеграла заменить S на свободную функцию Грина S0:

(1)( ) = ( − ) + 4 ( − )[− ˆ( )] ( − )

S x2, x1 S0 x2 x1 d xS0 x2 x ıeA x S0 x x1 .

Полученная функция Грина S(1) является причинной, если причинна S0(x2 − x1).

109. Элемент S-матрицы (амплитуды вероятности) перехода заряженного фермиона с 4-импульсом p1 и положительной энергией p10 = E1 > 0 в состояние с 4-импульсом p2 и энергией p20 = E2 > 0 при однократном взаимодействии с электромагнитным полем имеет вид:

t1 → −∞

134

¯(+) = [ (+)( )](†)

где ψp2 γ0 ψp2 x2 – эрмитовски сопряженная волновая (полевая) функция фермиона в указанном выше конечном состоянии; ψ(i)(x2) – волна, распространяющаяся в точку x2 из точки x1, причем при t1 → −∞ фермион находился в свободном состоянии, описываемом функцией:

Здесь u(p1) – биспинор Дирака, описывающий спиновое состояние фермиона (спиновый поляризационный индекс для краткости здесь опущен).

Волновую (полевую) функцию ψ(i)(x2) можно найти, используя причинную функцию Грина фермиона с учетом однократного взаимодействия с полем (см. задачу 104):

ψ(i)(x2) = d3x1S(1)(x2, x1)γ0ψp(+)1 (x1) = ψp(+)1 (x2)+

В проведенных расчетах использовалось свойство причинной функции Грина свободной частицы обеспечивать распространение состояния в пространстве-времени Минковского без искажения волновой (полевой) функции. Подставляя этот результат в выражение для Sp2,p1 , получаем:

= (2 )3 (3)(p − p ) + 4 ¯(+)( )[− ˆ( )] (+)( )

Sp2,p1 π δ 2 1 d xψp2 x ıeA x ψp1 x .

Здесь первое слагаемое в правой части равенства отвечает сохранению состояния частицы в отсутствии взаимодействия и обращается в нуль при p1 = p2. Второе слагаемое соответствует однократному взаимодействию с полем Aµ(x) и при p2 = p1 имеет

135

− ¯( ) ˆ( ) ( ) = ıeu√p2 A q u p1 .

2E22E1

= − ˆ( ) = ( ) ( )

Здесь q p2 p1, A q γµAµ q , Aµ q – компонента Фурье внешнего электромагнитного поля Aµ(x). Если это поле явно не зависит от времени, то Aµ(q) = 2πδ(E2 − E1)Aµ(q).

При взаимодействии с полем свободного фотона с 4-импульсом k и 4-вектором поляризации ε(µσ) в случае поглощения (излучения) этого фотона всюду в формулах следует вместо Aµ(x) подставить

пряженную функцию), где ω – энергия фотона. Тогда в случае излучения фотона:

Полученная амплитуда обращается в нуль для случая процессов излучения (поглощения) фотона свободным фермионом из-за обращения в нуль δ(4)-функции, так как не выполняются законы сохранения энергии и импульса.

110. Причинная функция Грина фермиона с учетом однократного взаимодействия с электромагнитным полем Aµ(x) найдена в задаче 108.

(1)( ) = ( − ) + 4 ( − )[− ˆ( )] ( − )

S x2, x1 S0 x2 x1 d xS0 x2 x ıeA x S0 x x1 .

Первое слагаемое в правой части соотношения описывает свободное распространение фермиона из точки пространства-времени Минковского x1 в точку x2 при условии t2 > t1. Это же слагаемое описывает распространение состояния с отрицательной энергией

136

Рис. 9

из точки x1 в точку x2 при условии t1 > t2, т.е. вспять по времени. Такой процесс интерпретируется как распространение антифермиона с положительной энергией из точки x2 в точку x1 нормально во времени (из прошлого в будущее). Второе слагаемое в правой части соотношения описывает следующие процессы во внешнем электромагнитном поле:

1)при t2 > t > t1 процесс однократного рассеяния в точке x фермиона, распространяющегося свободно из точки x1 в точку x и затем, после взаимодействия с полем, распространяющего-

ся свободно в точку x2 пространства-времени Минковского (рис. 9 а);

2)при соотношении времени t1 > t > t2 процесс распространения антифермиона из точки x2 в точку x1 с рассеянием в точке x (состояние фермиона с отрицательной энергией распространяется

вспять по времени из точки x1 в точку x2, испытывая взаимодействие с полем в точке x (рис. 9 б );

3)при t2, t1 > t процесс образования пары «фермион-анти-

137

фермион» внешним полем в точке x с распространением компонент пары из точки x в точки x2 (фермион) и x1 (антифермион) (рис. 9 в); формально этот процесс выглядит как распространение фермионного состояния с отрицательной энергией вспять по времени из точки x1 в точку x, где происходит взаимодействие с внешним полем, за счет которого фермион приобретает положительную энергию и распространяется далее свободно из точки x

вточку x2 нормально во времени;

4)при t2, t1 < t процесс аннигиляции пары «фермион-анти- фермион» во внешнем поле (рис. 9 г). При этом энергия пары

E1 + E¯2 = q0 передается полю. Отметим, что в стационарном поле Aµ(x) (отсутствует зависимость поля от времени) такой процесс невозможен, так как не выполняется равенство q0 = 0. Этот вывод является следствием известного правила: статическому внешнему полю можно передать импульс, но не энергию. Статическое внешнее поле не может также образовать пару «фермионантифермион» по той же причине, которая обсуждалась выше. Внешние поля, зависящие от времени, могут образовывать и поглощать пары «фермион-антифермион», если содержат частоты, соответствующие полной энергии излучаемой (поглощаемой) па-

ры, т.е. если выполняется равенство q0 = E1 + E¯, где q0 = ω –

2

частота, присутствующая в разложении потенциала поля в ряд (или интеграл) Фурье по частотам.

Заметим также, что переход фотона в пару «частица-анти- частица» в вакууме, как и аннигиляция пары в один фотон, запрещены законами сохранения энергии-импульса. Ранее уже отмечалось (см. задачу 9), что по тем же причинам невозможно излучение (поглощение) свободного фотона свободной частицей. Однако указанные процессы возможны, если начальная (конечная) частица или фотон – виртуальные, т.е. не распространяются вне области взаимодействия.

111. Пусть в точках x1 и x2 пространства-времени Минковского находятся фотон и заряженный фермион, которые, свободно распространяясь, взаимодействуют в точке x. Поскольку при однократном взаимодействии с заряженным фермионом фотон ли-

138

бо поглощается, либо излучается, из точки x в точку вторичного взаимодействия y будет распространяться только один фермион. В точке y этот фермион испускает фотон, а затем фотон и фермион распространяются в точки x3 и x4. Причинная функция Грина такого процесса выписывается в соответствии с диаграммой, изображенной на рисунке.

Gµσ (x3, x4, x2, x1) = d4xd4yDµν (x3 − y)S(x4 − y)×

× [−ıeγν ]S(y − x)[−ıeγλ]S(x − x2)Dλσ (x − x1),

где Dµν (z) и S(z) – причинные функции Грина свободного фотона и свободного фермиона с зарядом e.

Так как причинная функция Грина фермиона описывает распространение как частиц, так и античастиц, а причинная функция Грина фотона описывает распространение фотона в любой по времени последовательности событий, то функция Грина Gµσ (рис. 10) при различной временной последовательности событий отвечает следующим физическим процессам: 1) γ + e± → γ + e±

3) γ + γ → e+ + e− (образование пары «частица-античастица» двумя фотонами); 4) e± → e± + γ + γ (излучение двух фотонов фермионом или антифермионом); 5) γ +γ +e± → e± (поглощение двух фотонов заряженной частицей; 6) γ → γ + e+ + e− (образование

139

пары «частица-античастица» и фотона первичным фотоном); 7) γ+e+ +e− → γ (поглощение пары фотоном). Процессы 4 – 7 невозможны в вакууме из-за нарушения законов сохранения энергии и импульса.

112. Процессу (а) соответствует диаграмма рис. 11 а, согласно которой функция Грина процесса есть:

S(x2, x1) = d4xd4yS0(x2 − y)[−ıeγµ]

Dµν (y − x)S0(y − x)[−ıeγν ]S0(x − x1),

где S0(z), Dµν (z) – причинные функции Грина фермиона и фотона. Диаграмма рис. 11 а отвечает процессу взаимодействия фермиона с собственным электромагнитным полем во втором порядке по взаимодействию и называется диаграммой собственой энергии фермиона.

140