Ломоносова Сборник задач по квантовой електродинамике 2010

няет знак при перестановках биспиноров частиц a ↔ c или b ↔ d в исходном выражении. Поэтому, если точно таким же образом раскрыть правую часть исходного соотношения, то получится тот же результат, но отличающийся знаком от найденного выше. Эти расчеты позволяют убедиться в правильности соотношения Фирца.

5. Лагранжева формулировка и калибровочные симметрии

88. Как известно, лагранжианы в силу их ненаблюдаемости можно строить различными способами, лишь бы они приводили к правильным уравнениям движения – уравнениям Эйлера – Лагранжа. Наиболее простая форма лагранжиана свободных дираковских частиц имеет вид:

= ¯ − ¯

L0 ıψγµ∂µψ mψψ.

Введем в этот лагранжиан взаимодействие с электромагнитным полем, для чего заменим обычную производную ∂µ ковариантной производной Dµ = ∂µ + ıeAµ, где Aµ – 4-потенциал электромагнитного поля. Тогда лагранжиан запишется в форме:

= ¯ − ¯ = ¯ − ¯ − ¯( ) ( ) ( )

L ψγµDµψ mψψ ψγµ∂µψ mψψ eψ x γµψ x Aµ x .

111

Последнее слагаемое в полученной формуле представляет лагранжиан взаимодействия заряженных фермионов с электромагнитным полем. Переобозначим заряд электрона (−e) → e. Заряд выступает в лагранжиане взаимодействия в качестве константы связи. Полученный лагранжиан взаимодействия локален, т.е. все поля берутся в одной точке, и содержит два дираковских поля ψ и одно электромагнитное Aµ:

= ¯( ) ( ) ( ) = ( ) ( )

Lint eψ x γµψ x Aµ x ejµ x Aµ x .

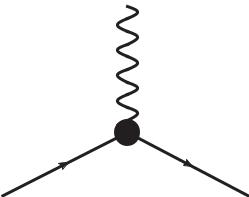
Это и есть лагранжиан взаимодействия квантовой электродинамики (КЭД). Если теперь полям фермионов сопоставить сплошные линии, а электромагнитному – волнистую линию, то в диаграммной технике КЭД в одной пространственно-временной точке x (вершине) будут пересекаться две сплошные и одна волнистая линия (рис. 5). Причем в соответствии с видом лагранжиана взаимодействия других вершин в КЭД не может быть.

Рис. 5

89. Рассмотрим лагранжиан свободных скалярных (S = 0) заряженных частиц (решений уравнения Клейна – Гордона) L0 = ∂µϕ (x)∂µϕ(x)−m2ϕ (x)ϕ(x) и введем в него взаимодействие с электромагнитным полем, заменив в нем обычную производную

112

∂µ «длинной», ковариантной производной Dµ:

L = Dµ ϕ (x)Dµϕ(x) − m2ϕ (x)ϕ(x) = ∂µϕ ∂µϕ − m2ϕ ϕ− −ıeAµϕ ∂µϕ + ıeAµ∂µϕ ϕ + e2ϕ ϕAµAµ = L0 + Lint,

Заменим в лагранжиане взаимодействия заряд (−e) отрицательным зарядом e и окончательно запишем Lint в форме:

Lint = ıe[∂µϕ (x)ϕ(x)−ϕ (x)∂µϕ(x)]Aµ(x)+e2ϕ (x)ϕ(x)Aµ (x)Aµ(x).

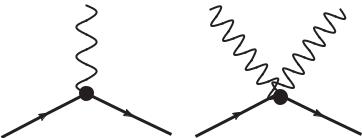
Слагаемое в квадратных скобках представляет плотность четырехмерного тока уравнения Клейна – Гордона jµ = ı[∂µϕ ϕ − ϕ ∂µϕ]. Нетрудно заметить, что лагранжиан взаимодействия скалярных заряженных частиц локален (т.е. все поля берутся в одной пространственно-временной точке x) и содержит наряду со слагаемым вида ’ток×на потенциал’ еще одно слагаемое, представляющее прямое взаимодействие двух скалярных и двух электромагнитных полей. Поэтому в диаграммной технике заряженных скалярных полей, кроме вершин, содержащих два скалярных и одно электромагнитное поле (пропорцианальных первой степени заряда e), присутствуют также вершины, где пересекаются два скалярных и два электромагнитных поля (рис. 6). Эти вершины пропорциональны заряду во второй степени и поэтому появляются, начиная со второго порядка теории возмущений.

113

−p2 −p2

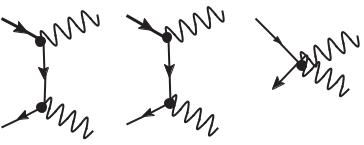
Рис. 7

90.Процесс аннигиляции пары скалярных заряженных частиц происходит во втором порядке теории возмущений и содержит три диаграммы. Первые две диаграммы аналогичны диаграммам КЭД (поскольку в конечном состоянии находятся два тождественных бозона – фотона, то в соответствии с квантовомеханическим принципом тождественности диаграммы процесса следует симметризовать, включив вторую диаграмму с переставленными фотонными квантовыми числами). Однако, в отличие от КЭД, здесь во втором порядке теории возмущений появляется еще одна диаграмма, где в вершине сходятся четыре линии – две линии, отвечающие скалярному полю, и две – электромагнитному (рис. 7).

91.Лагранжиан модели имеет вид:

Структура лагранжиана взаимодействия Lint предполагает, что в одной вершине пересекаются три скалярных поля. В теории с лагранжианом взаимодействия Lint = αϕ4 в одной вершине пересекаются четыре скалярных поля. Соответствующие фейнмановские диаграммы рассеяния скалярных частиц друг на друге в обеих моделях читателю предлагается построить самостоятельно.

92. Остановимся на более важном для квантовой электродина-

114

мики случае дираковских частиц (фермионов). Наиболее простая форма фермионного лагранжиана свободных полей имеет вид:

= ¯ − ¯

L0 ıψγµ∂µψ mψψ,

Подставим в уравнение Эйлера – Лагранжа (в качестве независи-

значения соответствующих производных

∂L

( ¯) = 0

∂ ∂µψ

и

∂L

¯ = ıγµ∂µψ − mψ. ∂ψ

Нетрудно видеть, что в результате получится уравнение Дирака (ıγµ∂µ −m)ψ = 0. Аналогично в случае лагранжиана свободных скалярных заряженных полей L0 = ∂µϕ ∂µϕ−m2ϕ ϕ, пользуясь в качестве независимых переменных ϕ и ∂µϕ , получим уравнение Клейна – Гордона. Если в обоих случаях использовать переменные ψ и ϕ и их производные, придем к соответствующим уравнениям

¯

для сопряженных функций ψ и ϕ .

93. Уравнение Эйлера – Лагранжа для массивных калибровочных бозонов имеет вид:

Запишем более подробно первое слагаемое уравнения Лагранжа:

=−12 ∂µ[2δµαδνβ ∂αBβ − δµβ δνα∂αBβ − δµαδνβ ∂β Bα] =

=−∂µFµν = −∂µ2 Bν (здесь учтено условие ∂µBµ = 0, в силу кото-

рого только три компоненты векторного поля являются независимыми). Тензор δµν = diag(1, 1, 1, 1).

115

Дифференцирование второго слагаемого в уравнении Лагранжа дает: = M 2Bν .

Таким образом, получим уравнение Прока для массивных калибровочных бозонов B со спином S = 1:

(∂µ2 + M 2)Bν = 0.

Каждая компонента 4-потенцила поля Bν подчиняется уравнению Клейна – Гордона.

94. Безмассовое векторное нейтральное поле, каковым является электромагнитное поле, вообще говоря, нельзя рассматривать как предельный случай массивного нейтрального поля, поскольку фотоны имеют на одно состояние поляризации меньше (два вместо трех у векторных мезонов). Этот факт приводит к некоторым формальным усложнениям, которые, однако, не связаны с вопросом калибровочной инвариантности. Требование калибровочной инвариантности для 4-потенциала электромагнитного поля Aµ имеет вид:

Aµ → Aµ = Aµ − ∂µχ(x),

где χ(x) – произвольная функция координат. Если бы фотон обладал отличной от нуля массой, то в его лагранжиане присутствовало бы слагаемое m2AµAµ, которое, очевидно не инвариантно относительно указанного калибровочного преобразования. Поэтому

вкалибровочных теориях массивные фотоны запрещены.

95.Заменяя в лагранжиане L0 производные в

Fµν = ∂µBν − ∂ν Bµ

на ковариантные производные Dµ = ∂µ + ıeAµ, мы вводим взаимодействие векторного массивного поля Bµ c электромагнитным полем с 4-потенциалом Aµ. При этом возникают вершины взаимодействия двух типов: а) в одной вершине пересекаются два бозонных поля и одно электромагнитное – эти вершины пропорциональны заряду e; и б) в одной вершине пересекаются два бозонных и два электромагнитных поля – эти вершины пропорциональны

116

e2. В частности, электромагнитное рассеяние двух массивных заряженных бозонов друг на друге в низшем порядке теории возмущений осуществляется посредством обмена одним фотоном.

96. Из левого и правого дираковских биспиноров (см. задачу

1−(γ5)2 = 0. Отсутствие правого нейтрино не позволяет сконструировать массовое слагаемое для нейтрино. Несмотря на то, что массивные нейтрино не запрещены ныне существующими теоретическими положениями, в электрослабой модели, например, это обстоятельство приводит к невозможности существования массы

унейтрино.

97.Майорановское нейтрино легко построить из дираковского нейтрино:

1

ψM = √2 [ψ + ψC ].

Действительно, (ψM )C = ψM . Здесь ψ и ψC – дираковское нейтрино и его зарядово сопряженная частица, т.е. античастица. Левое и правое майорановское нейтрино описывается функциями (см. задачу 85):

Массовое слагаемое в лагранжиане фермионов будет иметь вид:

117

Эта форма массового слагаемого отлична от дираковской и допустима только для нейтральной частицы – нейтрино. Если приписать нейтрино лептонное число L = 1, а антинейтрино L = −1, то такой лагранжиан не сохраняет лептонное число, так как содержит слагаемые, меняющие частицу на античастицу, при этом лептонное число изменяется на две единицы ∆L = |2|.

98.Для заряженных скалярных частиц (спин равен нулю) поле

ϕкомплексно. Лагранжиан имеет вид

L0 = ∂µϕ ∂µϕ − m2ϕ ϕ.

Будем рассматривать ϕ и ϕ как независимые поля. Лагранжиан, очевидно, инвариантен относительно глобального калибровочного преобразования

ϕ → eıeαϕ, ϕ → e−ıeαϕ ,

где α – действительная константа, e – заряд частиц. Данное преобразование меняет ненаблюдаемую как в квантовой механике, так и в квантовой теории поля, фазу волновой (полевой) функции и образует абелеву глобальную группу U (1). Это преобразование осуществляет вращение во внутреннем пространстве полей ϕ. Действительно, если

ϕ = ϕ1 + ıϕ2,

то

ϕ = eıeαϕ = ϕ 1 + ıϕ 2,

причем

ϕ 1 = ϕ1 cos (eα) + ϕ2 sin (eα),

а

ϕ 2 = −ϕ1 sin (eα) + ϕ2 cos (eα).

118

Глобальное преобразование U (1) не зависит от пространствен- но-временной точки x, поскольку параметр α является постоянной величиной.

Рассмотрим инфинитезимальное преобразование U (1) (α – бесконечно малая величина). Тогда:

ϕ → ϕ + ıeαϕ, ϕ → ϕ − ıeαϕ ,

∂µϕ → ∂µϕ + ıeα∂µϕ, ∂µϕ → ∂µϕ − ıeα∂µϕ .

И, следовательно,

δϕ = ıeαϕ, δϕ = −ıeαϕ , δ(∂µϕ) = ıeα(∂µϕ),

δ(∂µϕ ) = −ıeα(∂µϕ ).

В силу инвариантности лагранжиана относительно глобального преобразования U (1) его вариация должна обращаться в нуль:

бесконечно малом α вариации поля и его производных, получим:

Полученное слева выражение представляет 4-мерную дивергенцию тока, которая обращается в нуль. Использование явного выражения для лагранжиана скалярных заряженных частиц дает

!

α dxdµ eı ϕ ∂µϕ − ϕ∂µϕ = 0.

Выражение в квадратных скобках представляет электромагнитный ток Jµ скалярных заряженных частиц. А полученное равенство на основании произвольности α приобретает вид уравнения непрерывности для электромагнитного тока

dxdµ Jµ = 0.

119

или div J + ∂ρ∂t = 0 здесь ρ = J0 – плотность заряда. Интегрируя это соотношение по всему пространству, найдем

Следовательно, инвариантность относительно глобального преобразования U (1) приводит к сохраняющемуся электромагнитному току и закону сохранения заряда. Глубокий смысл полученного утверждения заключается в том, что заряд в данном объеме не увеличивается и не уменьшается сам по себе – за его изменение ответственны токи, втекающие или вытекающие из данного объема. Таким образом, электрический заряд локально сохраняется, и его значение можно использовать для характеристики элементарных частиц.

В приведенном выводе ничто не запрещает ограничиться использованием только электрического заряда. Элементарные частицы могут обладать также слабым или сильным (цветовым) зарядом, причем некоторые из этих зарядов связаны со своими сохраняющимися токами.

Полученное выражение для тока носит весьма общий характер. Оно представляет фундаментальное свойство квантовой теории поля: если система инвариантна относительно некоторого преобразования, то для нее существует определенная сохраняющаяся величина. В случае непрерывных преобразований это свойство теории поля можно сформулировать в форме теоремы Нётер: для системы, описываемой лагранжианом, любая непрерывная сим-

Учет высших порядков теории возмущений может привести к тому, что правая часть уравнения непрерывности для тока Jµ станет не равной нулю. Такие ненулевые члены называются «аномалиями». Требование, чтобы уравнение сохранения тока не содержало аномалий, служит важным соображением при построении

120