Ломоносова Сборник задач по квантовой електродинамике 2010

Функция Грина свободной частицы в импульсном представлении G0(p, p0) определяется соотношением:

здесь t = t2 − t1, x = x2 − x1. Для свободной частицы

1

G0(p, p) = −p0 − 2pm2 + ı ,

где → +0.

Интегральное уравнение для функции Грина G(x2 , x1) можно в случае «слабого» взаимодействия решить методом последовательных приближений с любой заданной точностью:

G(x2 , x1) = G0(x2 −x1) + d4xG0(x2 −x)[−ıV (x)]G0(x −x1)+

+d4xd4y G0(x2 −y)[−ıV (y)]G0 (y−x)[−ıV (x)]G0(x−x1 )+. . . .

Вимпульсном представлении, соответственно:

G(p2, p1) = (2π)4 δ(4)(p2 −p1)G0(p1)+ G0(p2)[−V (p2 −p1)]G0 (p1)+

31

где Ψi и Ψf – волновые функции начального и конечного состояний частицы.

В релятивистской квантовой механике функция Грина свободного уравнения Клейна – Гордона удовлетворяет уравнению:

(∂µ2 + m2)G0 (x2 − x1) = −ıδ(4) (x2 − x1).

Причинная функция Грина свободной частицы, подчиняющейся уравнению Клейна – Гордона, представляет фурье-образ в разложении:

и равна

1

G0(p) = −(p2 − m2 + ı )

при → +0.

Функция Грина фотона подчиняется уравнению:

∂2α2Dµν (x2 − x1) = ıgµν δ(4)(x2 − x1).

В импульсном представлении функция Грина фотона имеет вид:

Dµν (k) = gµν .

k2 + ı

Причинная функция Грина для свободного фермиона:

где

(pˆ + m)

S0(p) = −p2 − m2 + ı .

32

S0(x2 − x1) выражается через полевые функции полного набора состояний свободного уравнения Дирака ψ(±)p,λ следующим образом. При t2 > t1:

При t2 < t1:

Приведем выражения полевых функций через соответствующие функции Грина:

а) для частицы со спином 0:

←−→

ϕ(±)(x2) = ± d3x1G(x2, x1)(ı ∂t∂1 )ϕ(±)(x1);

(+) для k0 > 0 и t2 > t1; (−) для k0 < 0 и t1 > t2.

33

←−−→

A(µ±) (x2) = ± d3x1A(ν±) (x1) ı ∂t∂1 Dνµ(x1 − x2);

(+) для k0 > 0 и t1 > t2; (−) для k0 < 0 и t2 > t1. в) для фермиона (s = 12 ):

ψ(±)(x2) = ± d3x1S(x2, x1)γ0ψ(±)(x1);

(+)для p0 > 0 и t2 > t1; (−) для p0 < 0 и t1 > t2.

¯(±)( ) = ± 3 ¯(±)( ) ( );

ψ x2 d x1ψ x1 γ0S x1, x2

Задачи

101. a) Показать, что наличие фейнмановского доопределения (+ı ) в функции Грина свободного фермиона в импульсном представлении S0(p) = −p2−m2+ı приводит к правильной причинной функции Грина, т.е. при t2 > t1 – к вкладу частиц, а при обратном соотношении для времени – вкладу античастиц.

б) Получить сформулированный выше результат в случае функции Грина свободной скалярной частицы G0(p) в импульсном представлении.

102. Проверить равенства:

34

при t1 > t2.

Здесь ϕ±p – решения уравнения Клейна – Гордона с определенным импульсом и положительной (отрицательной) энергией; G0(x2 − x1) – причинная функция Грина свободного уравнения Клейна – Гордона.

103.Найти причинную функцию Грина уравнения Клейна – Гордона с учетом однократного взаимодействия скалярной заряженной частицы с электромагнитным полем.

104.Используя решение предыдущей задачи, установить вид амплитуды вероятности однократного взаимодействия скалярной частицы (мезона) с зарядом e с электромагнитным полем.

105.Определить амплитуду двукратного взаимодействия за-

ряженной скалярной частицы с электромагнитным полем за счет слагаемого e2A2µ в уравнении Клейна – Гордона.

106.Руководствуясь правилами Фейнмана и правилами, сформулированными в задачах 103 – 105 для простейших вершин взаимодействия скалярной частицы с электромагнитным полем, найти амплитуду комптоновского рассеяния фотона на мезоне и вычислить дифференциальное сечение этого процесса. Рассмотреть переход к пределу мягких фотонов (энергия первичного фотона ω1 m, где m – масса заряженной скалярной частицы).

107.Проверьте равенства:

где ψp±(x) – решения уравнения Дирака с определенным импульсом и положительной (отрицательной) энергией; S0(x2 −x1) – причинная функция Грина свободного уравнения Дирака. Иначе го-

35

воря, плоская волна с заданными квантовыми числами «переносится» свободной функцией Грина из пространственно-временной точки 1 в точку 2 с теми же квантовыми числами.

108.Найти причинную функцию Грина уравнения Дирака с учетом однократного взаимодействия заряженного фермиона с электромагнитным полем.

109.Используя решение задачи 108, установить вид амплитуды вероятности однократного взаимодействия заряженного фермиона с электромагнитным полем.

110.Установить, какие процессы описывает причинная функция Грина фермиона с учетом однократного взаимодействия с электромагнитным полем при различных возможных соотношениях между начальным и конечным моментами времени.

111.Выписать двухчастичную причинную функцию Грина заряженного фермиона и фотона в x-представлении, отвечающую двукратному взаимодействию между этими частицами. Указать, какие физические процессы описывает эта функция Грина.

112.Выписать причинные функции Грина в x-представлении для следующих процессов:

а) распространения фермиона с испусканием фотона и последующим его поглощением;

б) распространения фотона с превращением его в пару «фер- мион-антифермион» и последующей аннигиляцией этой пары в один фотон;

в) образования в вакууме фотона и фермион-антифермионой пары с последующей аннигиляцией этой пары и поглощением фотона в одной пространственно-временной точке.

36

7. Электродинамические процессы

Правила Фейнмана для вычисления элементов S-матрицы в КЭД

1. Внешнему фермиону (с положительной энергией) в конечном состоянии сопоставляется фактор: . На диаграмме Фейнмана внешнему фермиону в конечном состоянии сопоставляется сплошная линия, выходящая из вершины. Указанной линии приписывается 4-импульс p. Здесь p – 4-импульс фермиона, λ – спиральность – квантовое число удвоенной проекции спина на направление импульса, u¯λ(p) – дираковски сопряженный биспинор (точка всюду отвечает вершине взаимодействия).

u¯λ(p)

√2E

p

2. Внешнему фермиону в начальном состоянии сопоставляет-

uλ(p)

ся фактор √ . На диаграмме Фейнмана внешнему фермиону в

2E

начальном состоянии сопоставляется входящая в вершину сплошная линия; указанной линии приписывается 4-импульс p. Здесь uλ(p) – биспинор для состояний с положительной энергией.

uλ(p)

√2E

p

37

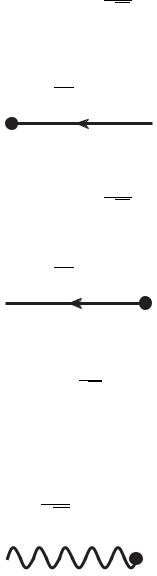
3. Внешнему антифермиону в конечном состоянии сопостав-

vλ (p)

ляется фактор √2E . На диаграмме Фейнмана ему сопоставляется входящая в вершину сплошная линия, указанной линии приписывается 4-импульс (−p). Здесь vλ(p) – биспинор для состояний с отрицательной энергией.

vλ(p)

√2E

−p

4. Внешнему антифермиону в начальном состоянии сопостав-

v¯λ (p)

ляется фактор √2E . На диаграмме Фейнмана ему сопоставляется выходящая из вершины сплошная линия, которой приписывается 4-импульс (−p).

v¯λ(p)

√2E

−p

5. Каждому поглощаемому реальному фотону сопоставляет-

ε(µσ)

ся фактор √2ω . На диаграмме Фейнмана поглощаемому фотону сопоставляется волнистая линия, входящая в вершину, с указанием 4-импульса фотона k. ε(µσ) – 4-вектор его поляризации; 4- векторный индекс µ совпадает с соответствующим индексом матрицы Дирака γµ в вершине поглощения, индекс (σ) отмечает тип поляризации поглощаемого фотона.

(σ)

√εµ2ω

(µ)

k

38

6. Излучаемому реальному фотону с 4-импульсом k и типом

поляризации (σ) сопоставляется фактор ε(µσ) . На диаграмме Фей-

√

2ω

нмана ему соответствует волнистая линия, выходящая из верши-

ны. ε(µσ)

√2ω

(µ)

k

7. Каждой вершине излучения (поглощения) фотона заряженным фермионом (антифермионом) сопоставляется фактор (−ıeγµ) (здесь e – заряд электрона). Кроме того, в каждой вершине 4- импульсы пересекающихся (входящих и выходящих) линий удовлетворяют закону сохранения 4-импульса, т.е. p1 + k = p2 или p1 −k = p2, где p1, p2 – 4-импульсы входящей и выходящей из вершины фермионной линии (для анифермионной линии p1 → −p1, p2 → −p2 ), k – 4-импульс поглощаемого или излучаемого в вер-

шине фотона. Каждой вершине соответствует δ(4)-функция вида:

(2π)4 δ(4)(p1 ± k − p2).

(−ıeγµ)(2π)4 δ(4)(p1 ± k − p2)

±k

39

8. Внешнему электромагнитному полю сопоставляется фактор (−ıeγµ)Aµ(q), где фурье-компонента 4-потенциала внешнего поля имеет вид Aµ(q) = d4xeı(qx)Aµ(x). Если поле Aµ(x) не зависит

явно от времени, то вершине взаимодействия с ним сопоставляется фактор (−ıeγµ)(2π)δ(E1 −E2)Aµ(q), где Aµ(q) = d3xe−ıqxAµ(x).

δ-функция отражает закон сохранения энергии фермиона (антифермиона), взаимодействующего с внешним полем. На диаграмме Фейнмана внешнему полю сопоставляется волнистая линия с крестиком на свободном конце.

(−ıeγµ)Aµ(q) – для нестационарного внешнего поля; q = p1 − p2;

(−ıeγµ)Aµ(q)(2π)δ(E1 − E2) – для стационарного внешнего поля; q = p1 − p2.

q

нмана виртуальному фермиону (антифермиону) сопоставляется сплошная линия, соединяющая две вершины. Здесь p – 4-импульс, переносимый фермионом. По 4-импульсам всех внутренних фермионных (антифермионных) линий проводится интегрирование

d4p (используя δ(4) -функции законов сохранения 4-импульсов

(2π)4 ı

в вершинах взаимодействия).

40