Ломоносова Сборник задач по квантовой електродинамике 2010

Разные относительные знаки между первым и вторым слагаемыми обусловлены статистикой Ферми, в соответствии с которой амплитуда должна быть антисимметричной при перестановке двух конечных (или начальных) электронов. Выражение для дифференциального сечения рассеяния неполяризованных электронов получается стандартным способом (см. задачу 114). Дифференциальное сечение определяется согласно следующей промежуточной формуле:

× δ(4)(p1 + p2 − p3 − p4)d3p3d3p4.

Здесь E и v – соответственно энергия и скорость каждого из электронов в ц-системе.

Окончательное выражение для дифференциального сечения в

где θ – угол рассеяния. При получении этого выражения были ис-

пользованы кинематические соотношения: (p1p2) = (p3p4) 2E2,

(p2p3) = (p1p4) 2E2 cos2 θ/2, (p1p3) = (p2p4) 2E2 sin2 θ/2 (пренебрегая слагаемыми порядка m2 ). В нерелятивистском приближении, когда E −m m, дифференциальное сечение в ц-системе

151

где p – импульс одного из электронов, v Ep – его скорость. 121. Результат предыдущей задачи для ультрарелятивистского

случая можно представить в релятивистски ковариантной форме

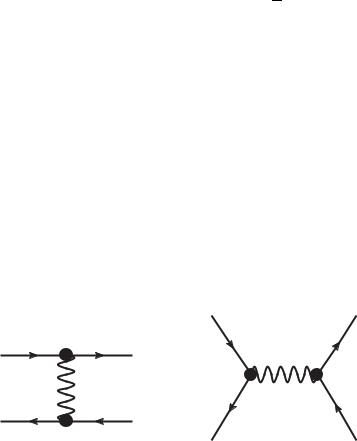
122. Фейнмановские диаграммы упругого e+e−-рассеяния изображены на рис. 16 a и б.

152

Первая из них аналогична диаграмме ee-рассеяния и отвечает обмену виртуальным γ-квантом между взаимодействующими зарядами. В нерелятивистском приближении эти диаграммы как в случае ee-, так и в случае e+e−-рассеяния, соответствуют кулоновскому взаимодействию. Диаграмма рис. 16 б описывает аннигиляционный механизм e+e−-рассеяния, когда электроннопозитронная пара переходит в виртуальный фотон, который в дальнейшем образует e+e−-napy в конечном состоянии. Этот механизм не имеет классического аналога, так как в классической физике (а также и в нерелятивистской квантовой механике) число частиц сохраняется на всех стадиях процесса взаимодействия. Аннигиляционный механизм – это чисто релятивистский квантовый эффект. Для того чтобы вычислить суммарную инвариантную амплитуду процесса e+e−-рассеяния, удобно воспользоваться свойством кроссинг-симметрии, которое состоит в том, что амплитуда ee-рассеяния превращается в амплитуду e+e−-рассеяния, если переставить один из конечных электронов в начальное состояние и заменить его 4-импульс на обратный по знаку. Ту же операцию следует выполнить для одного из начальных электронов, переставив его в конечное состояние с одновременной заменой знака 4-импульса на обратный. В результате такого кроссингпреобразования диаграмма рис. 15 а ee-рассеяния превращается в диаграмму рис. 16 а e+e−-рассеяния после замены p2 → −q4, p4 → −q2, p1 → q1 и p3 → q3. Последние две замены – это просто переобозначения 4-импульсов начального и конечного электронов. При такой же замене 4-импульсов диаграмма рис. 15 б ee- рассеяния превращается в диаграмму рис. 16 б для e+e−-рассея-

ния. Кроссинг-преобразование превращает биспинор u(p2) в биспинор u(−q4) = v(q4), а биспинор u(p4) в биспинор u¯(−q2) = −v¯(q2). Знак минус при этом возникает по следующей причине. Дираков-

ски сопряженный биспинор v¯(p) получается из биспинора u(p), описывающего состояние с положительной энергией, с помощью замены p → (−p) и последующим применением операции дираковского сопряжения: v¯(p) = u†(−p)γ0. В случае применения операции кроссинг-преобразования замена p → (−p) совершается в

153

аргументе дираковски сопряженного биспинора u¯(p). Перестановка указанных операций и приводит к изменению знака перед биспинором v¯(q2). Таким образом, инвариантная амплитуда процесса e+e−-рассеяния, полученная с помощью кроссинг-преобразования амплитуды e−e−-рассеяния (см. задачу120), имеет следующий вид:

Te+e− = −e2 (¯u(q3)γµu(q1))(¯v(q2)γµv(q4)) −

(q1 − q3)2

− (¯u(q3)γµv(q4))(¯v(q2)γµu(q1)) !. (q1 + q2)2

123. Диаграмма процесса рассеяния электрона на тяжелой точечной заряженной частице со спином s = 1/2, обладающей аномальным магнитным моментом µ, представлена на рис. 17.

p1 p2

q

q1 q2

Рис. 17

Верхняя линия отвечает электрону, нижняя – тяжелой частице. Вершина испускания фотона (в данном случае виртуального) с 4-импульсом q тяжелой частицей с зарядом (−e) и с аномальным магнитным моментом µ, кроме фактора ıeγα, содержит дополни-

тельно слагаемое вида 2ıeµ σαβ qβ , где M – масса тяжелой частицы,

M

σαβ = 12 (γαγβ − γβ γα), q = q1 − q2.

Инвариантная амплитуда на основе представленной на рисунке диаграммы представляется в виде:

154

Здесь ue и up – биспиноры, описывающие спиновые состояния электрона и тяжелой частицы. Часть тока перехода между начальным и конечным состояниями массивной частицы, связанную с аномальным магнитным моментом, можно упростить, используя

соотношения антикоммутации для γ-матриц и уравнение Дирака: qˆ1up(q1) = M up(q1); u¯p(q2)qˆ2 = M u¯p(q2).

1

u¯p(q2)σαβ qβ up(q1) = 2 u¯p(q2)(γαqˆ − qγˆ α)up(q1) =

1

= 2 u¯p(q2)[γαqˆ1 − γαqˆ2 − qˆ1γα + qˆ2γα]up(q1) =

1

= 2 u¯p(q2)[2γαqˆ1 − 2q1α + 2qˆ2γα − 2q2α]up(q1) =

= u¯p(q2)[2M γα − (q1α + q2α)]up(q1).

В результате инвариантная амплитуда T представляется в ви-

де:

Здесь Q = (q1 + q2).

Вычисление дифференциального сечения приводит к следую-

сечение, характеризующее угловое распределение электронов в л- системе, получается из приведенной формулы при учете следующих кинематических соотношений:

155

где E – энергия налетающего электрона; θ – угол рассеяния в л-системе; dΩ – элемент телесного угла, в котором наблюдается рассеянный электрон. Угловое распределение рассеянных электронов описывается формулой:

124. Двухфотонная аннигиляция электронно-позитронной пары описывается двумя фейнмановскими диаграммами, изображенными на рис 18. Диаграмма б отличается от диаграммы а перестановкой вторичных фотонов.

В силу требований статистики Бозе – Эйнштейна полная амплитуда процесса должна быть симметрична относительно перестановки тождественных частиц с целыми спинами (в данном случае фотонов). Поэтому амплитуды, отвечающие изображенным диаграммам, складываются:

156

Здесь u(p1), v¯(p2) – биспиноры, описывающие первичный электрон и позитрон; ε1,2 – 4-векторы поляризации вторичных фотонов с 4-импульсами k1 и k2. При замене ε1 на k1 или ε2 на k2 результат обращается в нуль, как и должно быть в силу свойства калибровочной инвариантности квантово-электродинамичес- ких процессов. Доказательство этого свойства проводится следу-

ющим образом: в знаменателях обоих слагаемых стоят выражения

(p1 −k1)2 −m2 = −2(p1k1), (p1 −k2)2 −m2 = −2(p1k2), а при замене

которого, действуя на биспинор u(p1), дает нулевой результат в силу справедливости уравнения Дирака. В числителе второго слага-

слагаемое которого, действуя справа на биспинор v¯(p2), дает нулевой результат, а слагаемое (p2k1) = (p1k2) в силу закона сохранения энергии-импульса. В результате оба слагаемых в квадратных скобках выражения для инвариантной амплитуды при замене ε1 на k1 взаимно уничтожаются. Аналогичный результат получается и при замене ε2 на k2. В отсутствии второй диаграммы б, которая обеспечивает выполнение требований Бозе-статистики, требование калибровочной инвариантности теории оказалось бы нарушенным.

125. Электрон и позитрон при определенных условиях образуют связанное состояние, подобное атому водорода, в котором роль протона выполняет позитрон. Такое связанное состояние называют позитронием. Основное состояние позитрония отвечает орбитальному моменту l = 0, то есть является S-состоянием. Могут осуществляться два типа S-состояний позитрония в соответствии с двумя возможными его спиновыми состояниями. Если полный спиновый момент позитрония равен нулю (синглетное состояние), то такое состояние называется парапозитронием и обозначается как 1S; состояние с квантовым числом полного спина, равным единице, называется ортопозитронием и обозначается как 3S. Позитроний является истинно нейтральным состоянием: при зарядо-

157

вом сопряжении возникает система, состоящая из тех же частиц, что и первоначальная. Такие состояния можно охарактеризовать определенными значениями зарядовой четности, которая в случае электромагнитных взаимодействий является «хорошим» квантовым числом. Зарядовая четность состояний позитрония устанавливается на основе обобщенного принципа Паули, который формулируется следующим образом: волновая функция системы фермионов, состоящей из частиц и такого же числа соответствующих им античастиц, должна быть антисимметрична относительно перестановки любой пары фермионов. Такая перестановка эквивалентна одновременной перестановке пространственных координат, спиновых переменных и электрических зарядов пары. Последняя операция в случае e+e−-пары отвечает зарядовому сопряжению C. Перестановка пространственных координат приводит к умножению волновой функции состояния на фактор (−1)l, где l – орбитальный момент данной пары; перестановка спиновых переменных приводит к фактору (−1)s+1, где s – квантовое число полного спина пары частиц. Произведение всех указанных факторов на фактор C, возникающий в результате перестановки зарядов e+e−-пары, должно давать результат (−1)l+s+1C = −1. Поэтому зарядовая четность системы «фермион-антифермион» определяется следующей формулой C = (−1)l+s. Соответственно зарядовая четность основного состояния парапозитрония Cpara = +1,

аортопозитрония Corto = −1. Позитроний является нестабильным образованием. Парапозитроний может аннигилировать в четное число фотонов, а ортопозитроний – в нечетное. Эти свойства обусловлены законом сохранения зарядовой четности в электро-

магнитных взаимодействиях (напомним, что зарядовая четность фотона Cγ = −1). Время жизни парапозитрония τpara 10−10c,

аортопозитрония τorto 10−7 c. Вероятность аннигиляции позитрония в единицу времени можно вычислить, если известно сече-

ние аннигиляции свободной электронно-позитронной пары σe+e−. Действительно, радиус первой боровской орбиты позитрония составляет a = 2a0 = mα2 , где a0 – боровский радиус атома водорода. Множитель 2 здесь возникает в силу того, что приведенная масса

158

позитрония вдвое меньше массы электрона. Согласно принципу неопределенности импульс одной из компонент пары составляет p a1 m. Поэтому процесс аннигиляции e+e−-пары, связанной в позитронии, можно рассматривать как аннигиляцию свободных частиц с очень малыми импульсами, но с определенным значением полного спина системы. Вероятность аннигиляции в единицу времени в единичном объеме для свободных частиц определяется по формуле w = vσe+e−, где v – относительная скорость аннигилирующих частиц. Однако эта вероятность усреднена по начальным спиновым состояниям электрона и позитрона, в то время как парапозитроний распадается на четное число фотонов, а ортопозитроний – на нечетное. Парапозитроний образует лишь одно из четырех возможных спиновых состояний позитрония, а ортопозитроний – остальные три (в соответствии с числом возможных значений проекции полного спина на ось квантования). Таким образом, при равновероятном образовании всех четырех возможных спиновых состояний позитрония усредненная вероятность аннигиляции составляет:

где w˜1 – вероятность аннигиляции из ортосостояния, а w˜0 – из парасостояния; wnγ – усредненные по спиновым состояниям e+e−- пары вероятности аннигиляции в n фотонов. В силу установленного выше следствия закона сохранения зарядовой четности:

– усредненные по спиновым состояниям e+e−-пары сечения про-

цессов двух- и трехфотонной аннигиляции при v → 0. Вероятности w˜0,1 связаны с вероятностями аннигиляции w0,1 связанных

159

состояний простым образом. Чтобы эту связь установить, нужно вспомнить, что вероятности w˜0,1 отвечают единичной плотности аннигилирующих частиц. В случае связанного состояния плотность вероятности обнаружить электрон и позитрон в одной

пространственной точке определяется квадратом модуля волновой функции S-состояния позитрония в точке r = 0: |Ψ(0)|2 = πa13 .

В результате находим искомые формулы для вычисления вероятностей:

двухфотонного распада парапозитрония

трехфотонного распада ортопозитрония

126. На основе полученной в задаче 124 инвариантной амплитуды процесса выражение для полного сечения реакции аннигиляции, усредненное по спиновым состояниям первичных частиц и просуммированное по спиновым состояниям вторичных фотонов:

где r0 = mα – классический радиус электрона, v0, ε0 – скорость и энергия одной из компонент пары в ц-системе. В нерелятивистском пределе (v0 1, ε0 − m m) из формулы для сечения σ2γ получаем следующее приближенное выражение:

Здесь v = 2v0 – относительная скорость электрона и позитрона в ц-системе. При выводе формул для сечения принято во внимание, что из-за тождественности фотонов следует учесть только

160