Ломоносова Сборник задач по квантовой електродинамике 2010

68.Из уравнения Дирака для электрона, взаимодействующего

сне зависящим от времени электромагнитным полем, получить в нерелятивистском пределе уравнение Паули.

69.Доказать, что оператор Гамильтона свободного уравнения Дирака не коммутирует по-отдельности с операторами компонент

момента количества движения и спина – сохраняется только полный момент J = L + S.

70.Найти релятивистские поправки порядка v2/c2 к нерелятивистскому гамильтониану атома водорода путем разложения гамильтониана уравнения Дирака, описывающего состояния электрона в кулоновском поле ядра, по степеням v/c. Провести классификацию полученных поправок.

71.Определить уровни энергии релятивистского электрона в постоянном магнитном поле.

72.Найти уравнения для дираковски сопряженных биспиноров u¯(p) и v¯(p) в импульсном представлении.

73.Найти решения уравнения Дирака для свободной покоя-

щейся частицы, которые являются одновременно собственными

функциями оператора Σz (ось z направлена вдоль вектора импульса частицы p в системе отсчета, где последняя движется).

74.В случае свободной дираковской частицы с 4-импульсом p показать, что операторы pˆ и sγˆ 5 в импульсном представлении

имеют общий набор собственных функций. 4-вектор sµ обладает следующими свойствами: s2 = −1, (sp) = 0.

75.Показать, что в системе отсчета, где дираковская частица обладает 4-импульсом p, 4-вектор s, определенный в задаче 74,

sγˆ 5 (см. задачи 74, 75), показать, что двухкомпонентные спиноры w и w , входящие в выражения для биспиноров u(p) и v(p), которые характеризуют спиновые состояния дираковской частицы, могут быть выбраны в виде собственных функций оператора проекции спина на направление ξ в системе покоя частицы (ξ – единичный вектор, определенный в задаче 75).

21

77.Показать, что вектор ξ (см. задачу 75) характеризует на-

правление вектора поляризации дираковской частицы в ее системе покоя2.

78.Для 4-вектора sµ, введенного в задаче 75, проверить соотношения s2 = −1, (sp) = 0.

79.Доказать, что матричный оператор спиральности (Σ|pp|) (где

p – импульс частицы) коммутирует с гамильтонианом H свободного уравнения Дирака. Сделать выводы о возможном выборе двухкомпонентных спиноров wλ, входящих в выражение для биспинора с положительной энергией.

80.Вычислить сумму λ=±1 uλ(p)¯uλ(p), где uλ(p) и u¯λ(p) – биспиноры свободной частицы со спином 1/2 и положительной

энергией, находящейся в состоянии с удвоенной проекцией спина

λна ось квантования3.

81.Вычислить сумму λ=±1 vλ(p)¯vλ(p), содержащую биспиноры свободной частицы со спином 1/2 с отрицательной энергией и удвоенной проекцией спина λ на ось квантования4.

82.Рассмотреть действие матричного оператора 12 (1 ± γ5) на биспинор свободной частицы со спином 1/2 с положительной энер-

гией и спиральностью λ (киральные состояния или левые и пра-

вые состояния). Перейти к пределу E m (E, m – энергия и масса частицы) и установить, какие спиральные состояния доминируют.

83. Выразить билинейную комбинацию u¯(p2)γ5u(p1) через

85. Показать, что антисостоянием к левому фермионному со-

2Вектором поляризации называется удвоенное среднее значение вектора спина дираковской частицы в данном состоянии.

3 λ=±1 wλ wλ † = I , где wλ – двухкомпонентный спинор, отвечающий спиновому состоянию с квантовым числом λ.

4 λ=±1 w λ w λ † = I , здесь w λ – двухкомпонентный спинор, содержащийся в выражении для биспинора vλ(p).

22

стоянию дираковской частицы будет правое состояние античастицы, т.е. (ψL)C = (ψC )R и наоборот (ψR)C = (ψC )L.

86. Показать, что матричный оператор Λ± = 12 (pˆ ± m)(1−γ5sˆ),

(где sµ – 4-вектор, определенный в задаче 75) отвечает следующим комбинациям биспиноров Λ+ = uλ=1(p)¯uλ=1(p),

Λ− = vλ=−1(p)¯vλ=−1(p).

87. Прямым вычислением доказать тождество Фирца:

[¯uaγµ(1+γ5)ub][¯ucγµ(1+γ5)ud] = −[¯uaγµ(1+γ5)ud][¯ucγµ(1+γ5)ub].

5. Лагранжева формулировка и калибровочные симметрии

Лагранжиан (лагранжева плотность) действительного скалярного поля ϕ(x), описывающий свободные бесспиновые нейтральные частицы, подчиняющиеся уравнению Клейна – Гордона, имеет вид:

1

L0(ϕ, ∂µϕ) = 2 [(∂µϕ)2 − m2ϕ2].

Лагранжиан комплексного скалярного поля ϕ(x), описывающий свободные бесспиновые заряженные частицы, подчиняющиеся уравнению Клейна – Гордона:

L0(ϕ, ∂µϕ, ϕ , ∂µϕ ) = (∂µϕ )(∂µϕ) − m2ϕ ϕ.

Здесь поля ϕ и ϕ рассматриваются как независимые при варьировании интеграла действия.

Лагранжиан свободных заряженных фермионов (поле ψ(x), спин 12 ), подчиняющихся уравнению Дирака, имеет вид:

( ¯ ¯) = ¯ − ¯

L0 ψ, ∂µψ, ψ, ∂µψ ıψγµ∂µψ mψψ.

¯

При варьировании действия поля ψ и ψ считаются независимыми.

23

Лагранжиан электромагнитного поля Aµ(x), подчиняющегося уравнениям Максвелла:

1

L0 = −4 Fµν Fµν ,

– тензор электромагнитного поля.

Fµν = ∂µAν − ∂ν Aµ.

Лагранжиан свободных массивных калибровочных бозонов, подчиняющихся уравнению Прока:

Fµν = ∂µBν − ∂ν Bµ.

Все динамические уравнения (Дирака, Клейна – Гордона, Максвелла, Прока) являются уравнениями Эйлера – Лагранжа для соответствующих полей:

¯

(или с заменой ψ на ψ или ϕ, ϕ , Aµ, Bµ), которые получают-

ся из принципа наименьшего действия для интеграла действия

S = L d4x.

Лагранжианы свободных заряженных полей инвариантны относительно глобального калибровочного преобразования U = eıeα, здесь e – заряд, α – любая действительная константа. Для заряженного скалярного поля глобальное калибровочное преобразование имеет вид:

ϕ → U ϕ, ∂µϕ → ∂µ(U ϕ) = U ∂µϕ, ϕ → U †ϕ , ∂µϕ → ∂µ(U †ϕ ) = U †∂µϕ .

Для заряженных фермионов калибровочное преобразование

¯

выглядит аналогично с заменой ϕ на ψ и ϕ на ψ. Глобальное

24

калибровочное преобразование унитарно U †U = 1 и зависит от одного действительного параметра α, элементы U (α1) и U (α2)

коммутативны. Совокупность таких элементов образует абелеву группу U (1).

Локальное калибровочное преобразование, согласующееся с принципами специальной теории относительности, является функцией пространственно-временной точки x в пространстве Минковского: U (x) = eıeχ(x), где константа α, соответствующая глобальному калибровочному преобразованию, заменяется произвольной функцией χ(x) пространственно-временной точки x.

Напомним, что электродинамика инвариантна относительно калибровочного преобразования вида: Aµ(x) → Aµ(x) − ∂µχ(x), где Aµ(x) – 4-потенциал электромагнитного поля.

Оба лагранжиана свободных заряженных частиц не инвариантны относительно локального калибровочного преобразования за счет неинвариантности производных

∂µψ(x) → ∂µ(U (x)ψ(x)) = U (x)[∂µ + ∂µχ(x)]ψ(x).

Чтобы скомпенсировать неинвариантность лагранжианов относительно локального калибровочного преобразования, следует ввести в них калибровочное векторное поле Aµ(x), заменив производную ∂µ новой ковариантной производной: Dµ = ∂µ + ıeAµ, где одновременно с локальным калибровочным преобразованием полей заряженных частиц 4-потенциал калибровочого поля Aµ(x) преобразуется по закону Aµ(x) → Aµ(x)−∂µχ(x). Это и есть калибровочная инвариантность электродинамики, а введенное нами поле Aµ(x) является электромагнитным. Теперь ковариантная производная будет преобразовываться при локальном калибровочном преобразовании так же, как и сама полевая функция ψ:

Dµψ(x) → [∂µ + ıe(Aµ(x) − ∂µχ(x))]U (x)ψ(x) = U (x)Dµψ(x).

ψили ϕ преобразуются следующим образом:

¯ → †( ) ¯( )

Dµψ U x Dµψ x .

25

«Поправленные» таким образом лагранжианы заряженных частиц, очевидно, будут инвариантны относительно локального калибровочного преобразования, а с другой стороны, эти лагранжианы уже описывают не свободные заряженные частицы, а частицы, взаимодействующие с электромагнитным полем.

Итак, введение электромагнитного поля в любую теорию сводится к замене производных ∂µ на «длинные», ковариантные производные:

Dµ = ∂µ + ıeAµ.

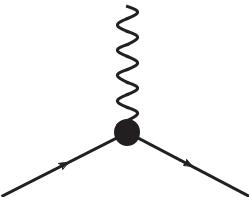
Рис. 1

Та часть вновь полученных лагранжианов, которая теперь содержит 4-потенциал электромагнитного поля, является лагранжианом взаимодействия заряженных частиц с электромагнитным полем. Таким образом, требование инвариантности лагранжианов относительно локальной калибровочной инвариантности приводит нас к теории взаимодействующих полей. А электромагнитное поле выступает в роли калибровочного, «компенсирующего» поля, которое необходимо ввести в лагранжианы заряженных полей материи, чтобы сделать их инвариантными относительно локального калибровочного преобразования U (1). Более того, часто

26

говорят: электромагнитное поле «порождается» локальной группой U (1). Лагранжианы взаимодействия уже не конструируются феноменологически, как это делалось раньше, а вытекают из требований локальной калибровочной инвариантности. Квантовая электродинамика (КЭД), в частности, является инвариантной относительно локальной группы U (1). Лагранжиан взаимодействия в КЭД (теории взаимодействия заряженных фермионов с электромагнитным полем) имеет вид:

Lint eψ ¯x γµψ x Aµ x .

= ( ) ( ) ( )

В графической фейнмановской интерпретации лагранжиан взаимодействия может быть представлен в виде диаграммы, «треххвостки», где в одной вершине (точке) сходятся два фер-

( ) ¯( )

мионных (антифермионных) поля ψ x , ψ x и одно – электромагнитное поле Aµ(x) (рис. 1).

Задачи

88.Ввести электромагнитное поле в лагранжиан свободных фермионов. Получить лагранжиан взаимодействия квантовой электродинамики и сделать заключение о структуре диаграммной техники в КЭД.

89.Вывести формулу для лагранжиана взаимодействия скалярных заряженных частиц с электромагнитным полем. Дать графическую интерпретацию найденного лагранжиана взаимодействия (см. также задачи 103 – 105).

90.Используя результат предыдущей задачи, изобразить гра-

фически процесс аннигиляции пары двух заряженных пионов в два фотона π− + π+ → 2γ в низшем порядке теории возмущений.

91.Рассмотреть модель массивного нейтрального скалярного поля ϕ(x), отвечающего гипотетическим мезонам F с самодействием Lint = λϕ3(x) (где λ – константа взаимодействия). Как бу-

27

дут выглядеть вершины в диаграммной технике этой теории? Нарисовать диаграммы, соответствующие рассеянию нейтральных частиц F друг на друге в низшем порядке теории возмущений по константе λ. Рассмотреть аналогичную модель гипотетического скалярного поля с самодействием Lint = αϕ4 (здесь α – константа взаимодействия).

92. Показать, что уравнения Клейна – Гордона и Дирака являются уравнениями Эйлера – Лагранжа, полученными из соответствующих лагранжианов свободных заряженных полей.

93. Из лагранжиана массивных калибровочных бозонов (квантов слабого взаимодействия B) L0 = −14 Fµν Fµν + 12 M 2Bν Bν (где Bν (x) – 4-потенциал слабого поля, Fµν = ∂µBν − ∂ν Bµ – тензор, аналогичный тензору электромагнитного поля, M – масса B-бозона), при условии, что ∂µBµ = 0, получить уравнение Эйлера – Лагранжа. Волновое уравнение для массивных калибровочных бозонов называется уравнением Прока.

94.В пределе M → 0 лагранжиан предыдущей задачи переходит в лагранжиан электромагнитного поля. Покажите, что требование калибровочной инвариантности электродинамики запрещает существование отличной от нуля массы фотона.

95.Ввести калибровочно-инвариантным способом электромагнитное поле в лагранжиан массивных калибровочных бозонов B:

L0 = −14 Fµν Fµν + 12 M 2Bν Bν . Указать, какие вершины возникают для взаимодействия векторных бозонов с электромагнитным полем.

96. Выразить массовое слагаемое дираковского лагранжиана

(− ¯( ) ( ))

L mDψ x ψ x через правые и левые компоненты дираковского поля. Показать, что поскольку в природе зарегистрированы только левые нейтрино и правые антинейтрино, то невозможно сформировать массовое слагаемое для дираковских нейтрино.

97. Существует альтернативное описание нейтрино, принадлежащее Э. Майоране. Основным свойством майорановского нейтрино является его совпадение с собственной античастицей. Пусть левая и правая компоненты майорановского нейтрино обладают определенными массами mML и mMR . Построить левые и правые

28

компоненты майорановского нейтрино из дираковского нейтрино и записать соответствующее массовое слагаемое в фермионном лагранжиане.

98.Покажите, что из инвариантности лагранжиана скалярных заряженных частиц L(ϕ, ϕ , ∂µϕ, ∂µϕ ) относительно инфинитезимального глобального калибровочного преобразования ϕ → eıeαϕ

(параметр преобразования α является бесконечно малой величиной) следует уравнение непрерывности для 4-вектора электромагнитного тока скалярных частиц и, как следствие, сохранение заряда. Это утверждение составляет содержание теоремы Нётер.

99.Докажите теорему Нётер в условиях задачи 98 для случая

( ¯ ¯)

лагранжиана спинорных частиц (фермионов) L ψ, ψ, ∂µψ, ∂µψ . 100. Пусть спинорное поле ψ является изотопическим дубле-

ψ(1)

том ψ = ψ(2) . Из свободного лагранжиана спинорного поля

построить лагранжиан, инвариантный относительно локальных

изотопических преобразований (так называемой группы SU (2)) U (x) = eı 12 τa Λa (x), то есть ψ(x) → U (x)ψ(x) (здесь τa ≡ σa – три матрицы Паули, a = 1, 2, 3). Показать, как меняются при

этом преобразовании калибровочные поля (поля Янга – Миллса), чтобы ковариантная производная осталась инвариантной относительно указанного преобразования.

6.Функции Грина

Внерелятивистской квантовой механике волновая функция в пространственно-временной точке 2 определяется через волновую функцию в точке 1 следующим образом:

Ψ(x2, t2) = d3x1K(x2, t2; x1, t1)Ψ(x1, t1) t2 ≥ t1.

Величина K(x2, x1) называется функцией распространения и при t2 = t1 удовлетворяет условию: K(x2, t1; x1, t1) = δ(3)(x2 − x1).

29

Причинная функция Грина уравнения Шредингера:

G(x2, x1) = θ(t2 − t1)K(x2, x1).

Функция Грина G удовлетворяет уравнению:

ı ∂t∂2 − H(x2) G(x2, x1) = ıδ(4)(x2 − x1),

где H(x2) = H0(x2)+ V (x2) – гамильтониан частицы в поле V (x2); H0(x) – гамильтониан свободной частицы. Эквивалентное интегральное уравнение:

G(x2, x1) = G0(x2 − x1) + d4xG0(x2 − x)[−ıV (x)]G(x, x1 ).

Здесь G0(x2 −x1) – функция Грина, отвечающая свободному распространению частицы и подчиняющаяся уравнению:

ı∂t∂2 − H0(x2) G0(x2 − x1) = ıδ(4) (x2 − x1),

Функция Грина K(x2, x1) может быть представлена через волновые функции полного набора стационарных состояний Ψn(x) гамильтониана H:

K(x2, x1) = Ψn(x2, t2)Ψn(x1, t1).

n

Для свободной частицы

30