Ломоносова Сборник задач по квантовой електродинамике 2010

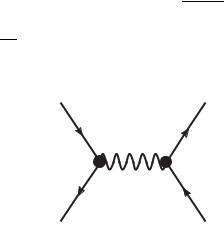
может образовать в вакууме электрон-позитронную пару. Однако фотон может образовать такую пару во внешнем поле, например, в кулоновском поле ядра, которому он может передать часть своего импульса.

Рис. 22

Две диаграммы рис. 22, описывающие этот процесс, топологически эквивалентны диаграммам для тормозного излучения фотона электроном в кулоновском поле ядра (см. рисунок задачи 131). Оба эти процесса связаны между собой соотношением кроссингсимметрии. Нетрудно понять, что из амплитуды тормозного излучения (см. задачу 131) амплитуда для рождения пары может

быть получена путем замены: p2 → p−, p1 → −p+, k → −k, u¯(p2) → u¯(p−), u(p1) → v(p+), ε → ε.

Тогда амплитуда для рождения пары запишется в виде:

где q = p+ + p− − k.

135.Доказательство калибровочной инвариантности проводится по образцу задачи 128.

136.Знаменатели амплитуды рассеяния для Комптон-эффекта на скалярной частице (см. задачу 106) совпадают со знаменателями для Комптон-эффекта на свободном электроне. Потому решение задачи 129 полностью справедливо и для случая скалярных заряженных бозонов.

171

137. Единственная диаграмма рассматриваемого процесса изображена на рис. 23.

p1 p2 q

Рис. 23

В соответствии с правилами Фейнмана, сформулированными в задаче 104, амплитуда процесса имеет вид: T = −e(p2 +p1)µAµ(q). Здесь Aµ(q) – Фурье-образ 4-потенциала электромагнитного поля, имеющего в случае кулоновского взаимодействия лишь одну временную компоненту:

а ее квадрат модуля:

|T |2 = Z2e4 (E1 + E2)2.

16p41 sin4 2θ

Подставим |T |2 в формулу для дифференциального сечения рассеяния:

172

E1 = E2. Полученная формула отличается от соответствующей формулы для рассеяния частиц со спином 1/2 отсутствием множителя (1 −v12 sin2 θ2 ) и полностью совпадает с классической формулой Резерфорда.

138. В силу тождественности частиц в конечном состоянии необходимо симметризовать амплитуду процесса так, чтобы две диаграммы, изображенные на рис. 24, складывались (а не вычитались, как в случае рассеяния тождественных фермионов).

p1 p3 p1 p4

Рис. 24

На основе этих диаграмм выражение для инвариантной амплитуды процесса имеет вид:

Дифференциальное сечение процесса вычисляется стандартным методом. Окончательно для углового распределения полу-

173

чим:

2

где β = mE 2 , E – энергия одной из частиц в ц-системе; v – ее скорость; m – ее масса; θ – угол рассеяния в ц-системе.

139. Процесс определяется единственной диаграммой рис. 25.

Дифференциальное сечение в ц-системе определяется выражением:

Здесь M и m – массы скалярной частицы и электрона; E – энергия каждой из частиц в ц-системе; θ – угол между импульсами позитрона и одной из скалярных частиц. Полное сечение образования пары скалярных частиц:

174

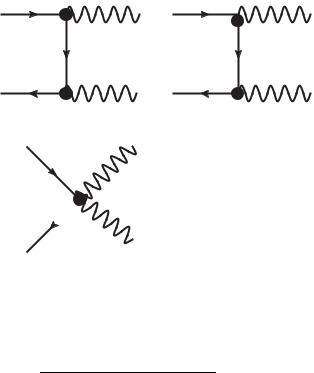
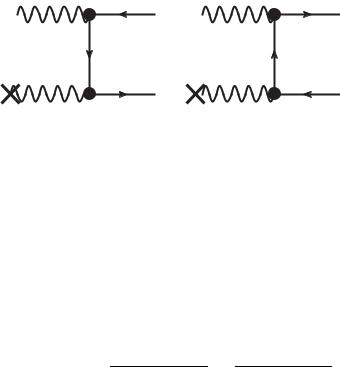
140. Процесс двухфотонной аннигиляции пары скалярных заряженных частиц описывается тремя диаграммами, изображенными на рис. 26.

−p2 k2 e+

Рис. 26

Амплитуда процесса такова (см. задачу 106):

В силу условия Лоренца: (ε1 k1) = (ε2k2) = 0, где ε1,2 – 4-векторы поляризации фотонов, k1,2 – их 4-импульсы. Тогда инвариантная

амплитуда T приобретает совсем простую форму:

175

Дифференциальное сечение процесса, вычисленное в переменных, относящихся к ц-системе, имеет следующий вид:

Здесь θ – угол между импульсом одной из компонент пары и импульсом одного из фотонов, E – энергия каждой из частиц в ц- системе. Полное сечение процесса двухфотонной аннигиляции пары

где β = mE .

141.Доказательство существования инфракрасной расходимости для тормозного излучения скалярных заряженных частиц полностью аналогично рассмотренному в задаче 131.

142.Для построения инвариантной амплитуды в нашем распоряжении имеются 4-векторы поляризации ε1 и ε2, а также 4- импульсы фотонов k1 и k2. С учетом псевдоскалярности распадающегося бозона амплитуда записывается в виде (4-вектор импульса π0-мезона p = k1 + k2):

T = e2f µνχρε1µε2ν k1χk2ρ.

Это выражение явно релятивистски и калибровочно инвариантно (замена ε1,2 → ε1,2 + λk1,2 не приводит к изменению амплитуды).

Феноменологическая константа f введена в амплитуду для соблюдения необходимой размерности. Вероятность распада определяется формулой:

176

Вычислим вероятность распада в единицу времени в системе покоя распадающейся псевдоскалярной частицы (масса частицы M ). Для этого удобно преобразовать амплитуду T к виду:

T= e2f µνχρε1µε2ν k1χpρ

T= e2f M µνχ0ε1µε2ν k1χ = e2f M 0ijlε1iε2j k1l.

Здесь i, j, l = 1, 2, 3. Полученное выражение представляется в трехмерной форме:

T = e2f M (k1[ε1ε2]).

Подставляя эту формулу в выражение для dw и проводя интегрирования с помощью δ-функции, находим:

dw = 14 α2f 2M |(k1[ε1ε2])|2dΩ,

где dΩ – телесный угол, в который испускается один из γ-квантов. Величину (k1[ε1ε2]) можно представить как ijlk1iε1j ε2l, где ijl – абсолютно антисимметричный единичный тензор третьего ранга в трехмерном пространстве. Векторы поляризации ε1,2 можно сразу же выбрать трехмерно поперечными (k1,2ε1,2 = k1,2ε1,2 = 0). Суммирование по поляризационным состояниям фотонов выполняется согласно формуле:

2

ε(jσ)ε(mσ) = δjm − kjkk2m .

σ=1

Вычислим величину

|(k1[ε(1λ) ε(2σ) ])|2 = ijlk1iε(1λj) ε(2σl ) mnsk1mε(1λn)ε(2σs) =

= ijl mnsk1ik1mδjnδls = ijl mjlk1ik1m =

177

При выводе этой формулы учтено, что k1 = −k2, ijlk1ik1j = 0. С учетом полученных результатов имеем:

dw = 18 α2f 2M 3dΩ.

Распределение γ-квантов изотропное. Интегрируя в силу тождественности γ-квантов по половине телесного угла, находим вероятность распада в единицу времени:

w = πα2f 2M 3 .

4

Поскольку вероятность распада в единицу времени имеет в системе единиц, где = c = 1, размерность массы, из полученного

результата для w вытекает, что константа f имеет размерность:

[f ] = [M −1].

143. Инвариантная амплитуда процесса V → P + γ, где V – массивный векторный мезон, P – псевдоскалярный мезон, выписывается из соображений релятивистской и калибровочной инвариантности с учетом псевдоскалярности волновой функции мезона Р :

T = ef αβγδ εαεβ k1γ k2δ .

Здесь εα, εβ – 4-векторы поляризации мезона V и γ-кванта соответственно; k1 – 4-импульс P , k2 – 4-импульс γ. Учитывая закон сохранения энергии-импульса p = k1 + k2 (p – 4-импульс V ) и антисимметрию тензора αβγδ по индексам γ и δ, в приведенной формуле допускается одна из следующих подстановок: k1γ → pγ или k2δ → pδ , которая упрощает вычисления в системе покоя частицы V .

144. Массивные векторные калибровочные бозоны (S = 1), кванты слабого взаимодействия W ± и Z0, играют ведущую роль в теории электрослабого взаимодействия. Уравнение Эйлера – Лагранжа, следующее из лагранжиана массивных калибровочных бозонов (см. также задачу 93), имеет вид:

∂µFµν + M 2Bν = 0,

178

где Bν – 4-потенциал векторного бозона, Fµν = ∂µBν − ∂ν Bµ. Полученное уравнение для 4-потенциала Bν выглядит следу-

ющим образом:

(∂α2Bν + M 2Bν − ∂µ∂ν Bµ) = 0.

Или:

(gµν (∂α2 + M 2) − ∂µ∂ν )Bµ = 0.

Вычислим дивергенцию ∂µ от обеих частей уравнения для Bµ. Так как первое и последнее слагаемые взаимно уничтожаются, получим M 2∂µBµ = 0, т.е.

∂µBµ = 0.

Благодаря данному условию из четырех компонент векторного поля независимыми являются лишь три. Для свободного массивного векторного поля Bµ εµe−ı(kx). В импульсном представлении условие равенства нулю дивергенции принимает вид:

kµεµ = 0,

в силу чего число независимых векторов поляризации уменьшается до трех. С учетом полученного условия уравнение для Bν упрощается и превращается в уравнение Прока:

(∂α2 + M 2)Bν = 0.

Запишем уравнение для Bν в импульсном представлении:

(−k2 + M 2)Bν (k) = 0.

Пропагатором (функцией Грина) векторной массивной частицы в импульсном представлении (как и в случае любых других частиц – фермионов, фотонов и пр.) является обратный оператор по отношению к оператору уравнения в импульсном представлении

179

−(k2 − M 2 + ı )−1 (с фейнмановским доопределением +ı ), умноженный на сумму по полному набору независимых поляризаций калибровочного бозона. (Вспомните, что в фермионном пропагаторе в числителе стоит фактор (pˆ+ m), который тоже представляет сумму по полному набору поляризаций фермиона (см. задачу 101), а числитель пропагатора фотона содержит фактор gµν , который отвечает сумме по полному набору поляризаций фотона с обратным знаком.) Запишем

3

ε(σ)µε(σ)ν = agµν + bkµkν .

σ=1

Действительно, правая сторона этого соотношения в силу симметричности тензора, стоящего в левой его части, выражается через симметричные тензоры gµν и kµkν . Умножим это выражение на gµν и, учитывая, что векторы поляризации с разными типами поляризации ортогональны друг другу ε(σ)ε(σ ) = −δσσ , получим

−3 = 4a + bM 2.

Далее, умножая сумму по поляризациям на kµ, с учетом условия kµεµ = 0 найдем

Окончательно пропагатор массивной вектрной частицы в импульсном представлении принимает вид:

Следует заметить, что опасной при высоких энергиях оказывается вторая, продольная часть пропагатора массивного векторного бозона ( kµkν ), которая резко растет с ростом энергии.

180