Ломоносова Сборник задач по квантовой електродинамике 2010

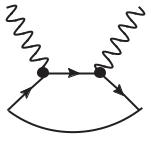
152. Получим дополнительные правила Фейнмана (см. также задачу 112) для вычисления фермион-антифермионной петли. Для этого рассмотрим элемент S-матрицы, соответствующий второму порядку теории возмущений.

(2) = 4 4 ¯ ( )(− ˆ( )) ( − )(− ˆ( )) ( )

Sf i d x3d x4ψf x4 ıeA x4 S0 x4 x3 ıeA x3 ψi x3 .

Фейнмановская диаграмма, соответствующая Sf(2)i , изображена на рис. 28.

Рис. 28

Чтобы получить фермион-антифермионную петлю, надо замкнуть фермионные концы диаграммы (см. рисунок). Аналитически это означает, что мы получим функцию Грина (пропагатор) с вкладом антифермионных состояний, причем при замыкании надо положить i = f и просуммировать по полному набору состояний с i = f ≡ n.

Здесь индексы m и k – матричные, они нумеруют строки и столбцы биспиноров. Знак (−) связан с присутствием в суммировании только состояний античастиц. Тогда элемент S-матрицы приобретет вид:

(2)= 4 4 [(− ˆ( )) ( − )(− ˆ( ))] [− ( − )]

S d x3d x4 ıeA x4 S0 x4 x3 ıeA x3 km S0 x3 x4 mk .

191

(2) = − 4 4 Sp [(− ˆ( )) ( − )(− ˆ( )) ( − )]

S d x3d x4 ıeA x4 S0 x4 x3 ıeA x3 S0 x3 x4 .

Итак, дополнительные правила Фейнмана для фермион-антифер- мионной петли:

(a)Умножение на (-1) для каждой петли;

(b)Взятие следа по спинорным индексам.

Используя полученные правила Фейнмана, для поляризационного оператора Πµν получим следующее выражение в импульсном представлении:

Здесь одна δ-функция закона сохранения 4-импульса, стоящая в одной из вершин диаграммы, используется для взятия интеграла по 4-импульсам какой-либо из фермионных линий, а другая будет присутствовать общим множителем, отражающим закон сохранения энергии-импульса всего процесса в целом. Ее мы опустили. Перемножив все множители в числителе и взяв от них по общим правилам след, получим следующее выражение:

Нетрудно заметить, что полученное выражение расходится квадратично.

153. Для дальнейшего вычисления формулы для Πµν , полученной в предыдущей задаче, воспользуемся фейнмановской параметризацией. «Трюк», придуманный для этой цели Фейнманом, основан на очевидном тождестве

192

Положим в интеграле для Πµν a = (p − k)2 − m2, b = p2 − m2 (малую добавку ı пока опустим).

Преобразуем выражение в знаменателе, дополнив его до полного квадрата:

((p − k)2 − m2)z + (p2 − m2)(1 − z) =

=(p2 − 2pkz + k2z − m2) + k2z2 − k2z2 =

=(p − kz)2 + k2z(1 − z) − m2.

Введем новую переменную интегрирования p˜ = p−kz. С помощью этой переменной выражение для Πµν преобразуется к виду:

F = −2p˜µkν z − 2p˜ν kµz + p˜µkν + p˜ν kµ + pk˜ (2z − 1)gµν . Интегралы, содержащие в числителе слагаемые, линейные по p˜, обращаются в нуль, так как являются интегралами от нечетной функции по всему импульсному 4-пространству. Интеграл от первого слагаемого в числителе Πµν можно упростить. Так как выражение p˜µp˜ν симметрично по индексам µ и ν, то результат интегрирования должен содержать симметричный тензор, а единственным симметричным тензором в пространстве Минковского является метрический тен-

193

занного выше Πµν приобретает вид:

[( p˜2 + m2)gµν + 2kµkν z(1 − z) − k2gµν z(1 − z)]

2 .

(p˜2 + l)2

154. Потребуем калибровочной инвариантности поляризационного оператора Πµν (см. задачи 124, 128), то есть потребуем, чтобы kν Πµν = 0:

Только благодаря калибровочной инвариантности исчезает квадратично расходящееся слагаемое, пропорциональное

d4p˜ 2p˜2 2 , линейной расходимости тоже не возникает (см. зада-

(p˜ +l)

чу 153) – остается только логарифмическая расходимость. В КЭД в общем случае не существует расходимостей выше логарифмических. Расчет петлевых диаграмм представляется громоздкой, но хорошо разработанной процедурой. Наряду с изложенным здесь методом фейнмановской параметризации существуют и другие

194

способы вычисления расходящихся интегралов, например, метод размерной регуляризации, процедура вычитания бесконечностей

идругие.

Сиспользованием калибровочной инвариантности выражение для поляризационного оператора упрощается:

Из сравнения полученного выражения с общим видом поляризационного оператора, сконструированного в задаче 151, следует, что полученное здесь выражение содержит правильную тензор-

ную структуру (kµkν − k2gµν ), а оставшийся интеграл определяет

Π0(k2):

155. Вычислим интеграл для Π0(k2), полученный в предыдущей задаче. В подынтегральной функции p˜2 = p˜20 − p˜21 − p˜22 − p˜23, d4p˜ = dp˜0dp˜1dp˜2dp˜3. Повернем контур интегрирования по переменной p˜0 с действительной оси на угол π2 против часовой стрелки в комплексной плоскости p˜0, как показано на рис. 29. Такой поворот называется поворотом Вика. При этом повороте полюса подынтегральной функции (см. задачу 152) в выражении для Πµν не пересекаются контуром интегрирования, и поэтому поворот математически корректен. Крестиком на рисунке отмечены полюса

подынтегральной функции. Положим p˜0 = ıp˜4, тогда d4p˜ = ıd4p , p˜2 = −(p˜21 + p˜22 + p˜23 + p˜24) = −p 2. Пространство для 4-вектора p

стало евклидовым. Соотношение для Π0(k2) запишется в виде:

195

Im p˜0

π

2

Re p˜0

евклидовом пространстве. Обозначим 4-объем в таком пространстве V4 = C4p4, dV4 = 4C4p3dp. Чтобы найти C4, воспользуемся интегралом:

С другой стороны, тот же интеграл можно вычислить в сферических координатах в 4-мерном пространстве

Сравнивая выражение для J, вычисленное двумя способами, найдем C4 = π22 .

После этого вычисление искомого интеграла I не представляет

196

Второй интеграл в полученном выражении не содержит расходимости, а первый расходится логарифмически. Заменим в нем верхний бесконечный предел интегрирования большим «обрезающим» квадратом импульса L2 и ограничимся при вычислении основным логарифмически расходящимся слагаемым:

Вводя α = e2/4π и проведя интегрирование по z в первом слагаемом, окончательно получим:

156. В случае низких энергий |k2| m2 в формуле для Π0(k2),

выведенной в предыдущей задаче, можно упростить второе слагаемое ln [1 − (k2/m2)z(1 − z)] ≈ (−k2/m2)z(1 − z), и Π0(k2) принимает вид:

197

Экранирование заряда, происходящее за счет поляризации вакуума, имеет физические следствия и при низких энергиях. В случае достаточно малых |k2| кулоновское взаимодействие, например, можно приближенно записать в виде:

Данный результат был впервые получен Уилингом. В конфигурационном пространстве для бесконечно тяжелого ядра с зарядом (−Ze), расположенного в начале координат, это выражение дает следующую поправку:

Разложение потенциала в окрестности нуля в конфигурационном пространстве приводит к сингулярности. Однако нас обычно интересует лишь среднее значение потенциала в невозмущенных состояниях, на котором не сказывается замена реальной поправки, имеющей форму острого пика при малых r, на δ-функцию. Следует отметить, что это усиление при малых r согласуется с представлением о том, что на малых расстояниях восстанавливается неэкранированное взаимодействие с затравочным зарядом. Лэмб обнаружил, что поправка, связанная с поляризацией вакуума, понижает s-уровень водородоподобного атома на величину порядка -27 МГц.

При высоких энергиях |k2| m2 второе слагаемое в Π0(k2) упрощается следующим образом:

(в конкретных приложениях −k2 ≥ 0). Тогда Π0(k2) дается выражением:

198

Обсуждение полученных формул будет проведено в задачах 157

–158.

157.Определим квадрат физического, наблюдаемого заряда

как коэффициент при кулоновском статическом потенциале 4πr1 на больших расстояниях, то есть в случае мягких кулоновских фотонов с |k| → 0. Очевидно, что мягкий фотон с большой длиной волны «видит» электрон в целом, заэкранированный частицами, образующимися в процессе виртуального образования пар окружающим его фотонным полем. Этот заряд мы будем называть фи-

2

зическим, перенормированным зарядом, для которого 4eπ = 1371 . Рассмотрим процесс рассеяния электрона кулоновским полем

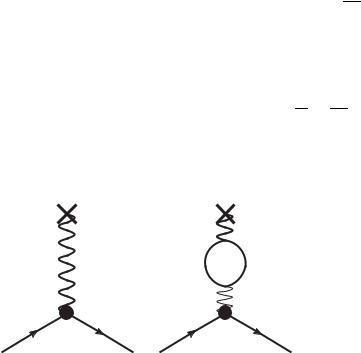
ядра с учетом образования одной петли поляризации вакуума – первой неисчезающей радиационной поправки к фотонному пропагатору (рис. 30 а, б ).

Здесь A0(k) = −Zk2e , k = p2 − p1. Покажем что продольная часть поляризационного оператора, пропорциональная kµk0, не дает вклада в рассматриваемый процесс. Действительно,

199

kµu¯(p2)γµu(p1) = u¯(p2)(pˆ2 − pˆ1)u(p1) = 0 в силу уравнений Дирака: pˆ1u(p1) = mu(p1), u¯(p2)pˆ2 = mu¯(p2).

После подстановки поперечной части Πµ0(k) амплитуда приобретает вид:

За счет поляризационной петли произошло видоизменение фотонного пропагатора D(0) = k12 → k12 [1 − Π0(k)]. Однако физиче-

ски эффект поляризации вакуума приводит к изменению заряда за счет его экранирования, т.е. к перенормировке заряда. Поэтому изменение фотонного пропагатора при |k2| → 0 фактически перенормирует заряд электрона, превращая его из ненаблюдаемого, затравочного заряда e0 в физический, наблюдаемый заряд

Полученная формула определяет перенормировку заряда в однопетлевом приближении, а величина Z3 = [1 − Π0(0)] называется константой перенормировки в однопетлевом приближении.

Заметим, что реальный фотон не индуцирует виртуальных токов e+e− в вакууме (см. пояснение в конце задачи 158).

158. Происхождение перенормировки связано с тем обстоятельством, что состояние системы в теории возмущений описывается с помощью невозмущенных, «голых» полевых функций, хотя в реальном физическом мире каждая заряженная частица обладает своим полем, и мы не можем выключить взаимодействие между различными полями. По этой причине возникают поправки к «затравочным» заряду и массе. Поэтому, так как на опыте могут наблюдаться только физические заряд и масса, мы должны выражать наблюдаемые величины в терминах их перенормированных значений.

В некотором смысле вопросы расходимостей и перенормировки разделены. Однако все локальные релятивистские теории поля

200