Статы Экзамен / Статы / statukr

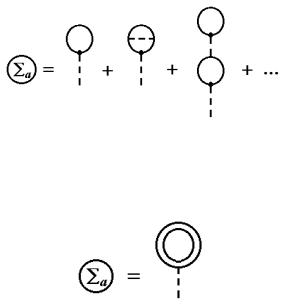
лінія приєднується до вхідної і вихідної ліній. Позначимо суму таких діаграм a (рис. 11.9). Суму інших діаграм

позначимо b .

Рис. 11.9. Діаграми для функції a

З рис. 11.9 видно, що підсумовування частин діаграм без зовнішньої штрихової лінії еквівалентно подвоєнню петлі, показаному на рис. 11.10.

Рис. 11.10. Графічне зображення доданка a

Подвійній петлі відповідає точний вираз для густини електронів n ,T . У результаті маємо

Процедура обчислення звелася до підсумовування нескінченної сукупності діаграм для b .

11.8. Наближення Хартрі – Фока

На жаль, підсумувати всі діаграми, які входять у b , для

реальної системи взаємодіючих частинок неможливо. Помітний прогрес у теорії систем багатьох частинок був дося-

430

гнутий лише шляхом вибіркового підсумовування певної сукупності діаграм, важливих у даній задачі. Тут ми розглянемо найпростіший приклад такого підсумовування.

У розкладі обмежимося діаграмами на рис. 11.11. Така апроксимація називається наближенням Хартрі–Фока.

Рис. 11.11. Діаграми для у наближенні Хартрі – Фока

Перший доданок на рис. 11.11 обумовлений прямою міжчастинковою взаємодією, а другий – обмінною. Подвійна лінія в другому доданку означає, що між актами взаємодії частинка рухається в полі інших частинок.

Використовуючи правила відповідності, запишемо суму на рис. 11.11 в аналітичному вигляді

де p і s – імпульсна та енергетична змінні, які зіставля-

ються з подвійною лінією в другому доданку на рис. 11.11. Функція (11.97) у розглянутому наближенні не залежить від s . Вхідна в (11.97) сума пов'язана з функцією розпо-

Зрівняння Дайсона (11.95) випливає, що функція Гріна

внаближенні Хартрі – Фока збігається з вільною функцією

431

але тепер залежність енергії «частинки» від імпульсу E p стає більш складною:

Ми прийшли до картини незалежних «частинок» із законом дисперсії (11.100), ідеальний газ яких імітує систему взаємодіючих частинок. Такі «частинки» називаються квазічастинками. Їх спектр збігся з полюсом аналітичного продовження функції (11.99) з дискретних точок zs i s

на площину комплексної енергії. Цей результат справедливий і в більш складних випадках. Полюс, як правило, виявляється комплексним: Ep i p . Величина p обумовлює

згасання квазічастинок у системі взаємодіючих частинок. З формули (11.100) видно, що в наближенні Хартрі – Фока згасання відсутнє.

Поняття квазічастинки – одне з найважливіших у статистичній фізиці. Її можна уявляти собі як частинку, оточену хмарою інших частинок. Наприклад, у системі електронів на фоні позитивного заряду електрон відштовхує від себе інші електрони. У результаті навколо електрона утворюється хмара позитивного заряду, яка рухається за ним. Позитивний заряд екранує заряд електрона, зменшуючи його взаємодію з іншими електронами.

Використовуючи результати підрозділу 11.3 і формулу (11.99), переконуємося в тому, що функція розподілу f

дорівнює

432

Величини E p і f p можуть бути визначені з рівнянь

(11.100) і (11.101), які необхідно розв’язувати сумісно. Застосуємо ці рівняння до виродженого електронного газу.

Компонента Фур'є енергії кулонівської взаємодії електронів (6.90) при q 0 стає нескінченною. Однак доданок

0 n у (11.100) можна не враховувати, тому що він ком-

пенсується рівномірно «розмазаним» позитивним зарядом, який забезпечує електричну нейтральність системи. Щоб переконатися в цьому, запишемо гамільтоніан електрон– електронної взаємодії (6.80) у вигляді

Якщо скористатися комутаційними співвідношеннями (6.83), доданок з q 0 у формулі (11.102) стане рівним

– оператор числа електронів. Власне значення оператора

(11.103) дорівнює

де враховано N 1, а нульова компонента Фур'є функції

433

Вираз (11.104) збігається з енергією статичного однорідно розподіленого в об’ємі V негативного заряду. Точно таку ж енергію має і позитивний заряд. До неї необхідно додати енергію взаємодії електронів з фоном позитивного заряду. Вона в два рази більша величини (11.104) і відрізняється від неї знаком. Отже, ці три доданки у виразі для енергії компенсуються.

При нульовій температурі розподіл (11.101) перетворюється в сходинку Фермі, а обмінний внесок в енергію квазічастинки (11.100) виявляється рівним

де pF – імпульс Фермі (5.10), а – функція Хевісайда

(1.7). Можна показати, що обмінна енергія виродженого електронного газу в наближенні Хартрі – Фока дорівнює

обм 4

де N – повне число електронів у системі. Цей вираз збігається з формулою (6.66), отриманою іншим методом.

Розглянемо внесок хартрієвського доданка 0 n у тиск

газу нейтральних частинок, які підкоряються законам класичної механіки. У цьому наближенні обмінний внесок в енергію (11.100) відсутній. Використовуючи термодинамічну тотожність (2.92), представимо похідну тиску P за хімічним потенціалом у вигляді

434

де n – густина газу. При фіксованій температурі звідси одержуємо

Для обчислення густини скористаємося розподілом Максвелла – Больцмана (4.26):

Диференціюючи це співвідношення при постійній температурі і з огляду на (11.107), одержуємо

dP kTdn 12 0 d n2 .

Після інтегрування цього рівняння знаходимо

де враховано P 0 при n 0. Ми одержали рівняння Ван- дер-Ваальса (6.33), у якому власні розміри частинок не враховані. Постійна a, яка враховує взаємодію частинок,

дорівнює

a 12 0 2 0 drr2 r ,

якщо частинки слабо притягуються одна до іншої на будьякій відстані r.

11.9. Ефективна взаємодія. Поляризаційний оператор

Діаграми для власно-енергетичної функції можна спростити, якщо ввести поняття ефективної взаємодії частинок. Для цього розглянемо штрихові лінії на рис. 11.5, 11.6. Видно, що можна виділити частини діаграм, які містять

435

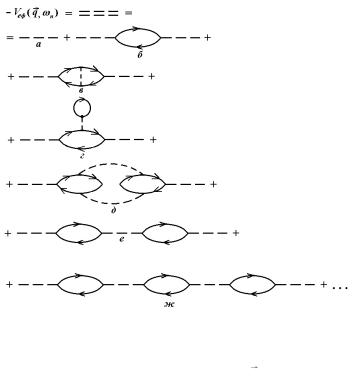
одну вхідну і одну вихідну штрихові лінії. Їх можна обчислювати самостійно, використовуючи отримані в підрозділі 11.6 правила відповідності, а потім вставляти в діаграми для функції Гріна або власно-енергетичної функції. Діаграми, які мають одну вхідну та одну вихідну штрихові лінії взаємодії, називаються поляризаційними діаграмами. Їх сума називається ефективним потенціалом взаємодії. Зображуючи його подвійною штриховою лінією, одержуємо для цієї суми діаграми на рис. 11.12.

Рис. 11.12. Діаграми для ефективної взаємодії

Зіставляючи ці діаграми з аналітичними виразами, ми мо-

дає вхідній і вихідній лініям взаємодії. Тоді в дужках залишиться сума діаграм без штрихових кінців. Такі частини діаграм називаються поляризаційними частинами. Серед

436

поляризаційних частин є неприводимі і приводимі. Неприводимою називається поляризаційна частина, яку не можна розбити на дві незв'язані поляризаційні частини шляхом видалення однієї лінії взаємодії. На рис. 11.12 діаграми б д мають неприводимі поляризаційні частини. Поляризаційні частини діаграм е, ж приводимі. Сума всіх непри-

водимих поляризаційних частин називається поляризаційним оператором. Позначимо його буквою і зобразимо фігурою на рис. 11.13. Тут показано декілька діаграм для поляризаційного оператора.

Рис. 11.13. Діаграми для поляризаційного оператора

Як і в підрозділі 11.7, поляризаційний оператор дозволяє представити ряд на рис. 11.12 у вигляді

Зіставляючи окремі члени цього ряду з аналітичними виразами, одержуємо

437

Формули (11.108) і (11.109) пов'язують ефективну взаємодію із взаємодією ізольованих частинок і з поляризаційним оператором. Функція (11.110), задана для парних мацубарівських частот, називається мацубарівською діелектричною функцією. Її аналітичне продовження з дискретної сукупності точок на верхню напівплощину комплексної частоти дає запізнюючу функцію

регулярну у верхній напівплощині. Вона є окремим випадком узагальненої сприйнятливості, розглянутої в підрозділі 7.9. Формула (11.109) описує зменшення кулонівської взаємодії електронів у середовищі, обумовлене її поляризацією кулонівським полем. З цієї причини ефективний потенціал (11.109) називається екранованим потенціалом.

Використовуючи ефективний потенціал, можна спростити ряд для власно-енергетичної частини. Щоб переконатися в цьому, розглянемо першу діаграму на рис. 11.7 для власно-енергетичної частини. У розкладі поряд з цією діаграмою є і такі, які відрізняються від неї заміною штрихової лінії на щось більш складне. Штрихова лінія може бути ускладнена так, як показано на рис. 11.12. Підсумовуючи всі такі діаграми, одержимо діаграму на рис. 11.14, яка відрізняється від вихідної заміною одинарної штрихової лінії подвійною.

438