14-es_1 / Высшая математика (РТФ) / умк_Вакульчик_Опред интеграл

a

Замечание 7.8.4. Теоремы 7.8.1, 7.8.2 и их следствия можно при- менять, если знать сходимость интегралов-эталонов. В качестве эталона может выступать

Изучим сходимость еще одного эталонного интеграла

31

сходится, то заданный несобственный интеграл сходится по следствию 7.8.1.

Пример 7.8.5. Исследовать на сходимость несобственный инте-

резке [a,b], за исключением конечного числа точек, вблизи которых функ-

ция неограниченна (имеет разрыв второго рода). Предположим, что f ( x)

неограниченна в левом конце х = а. Тогда несобственным интегралом второго рода называют

ках отрезка [a,b], кроме правого конца х = b, и неограниченна в правом конце х = b, то несобственным интегралом второго рода называют

32

Определение 7.9.4. Если в левой части (7.9.1) – (7.9.3) все преде- лы существуют и конечны, то несобственный интеграл называется сходя-

щимся, в противном случае – расходящимся.

Геометрический смысл несобственного интеграла второго рода.

асимптотой x = c , как показано на рис. 7.9.1

Признаки сходимости несобственного интеграла второго рода.

Замечание 7.9.1. Признаки сходимости несобственных интегра- лов второго рода по формулировке совпадают с признаками сходимости несобственных интегралов первого рода, только сравнение идет с эталона- ми в окрестности точек разрыва. В качестве интегралов-эталонов могут быть использованы интегралы вида

Решение. Подынтегральная функция терпит на отрезке интегрирова- ния разрыв второго рода в точке x = 1.

Первый способ. Вычислим заданный Н. И. по определению 7.9.3. Будем иметь

33

Имеем, что m = 2 < 1, значит, исходный интеграл сходится. 3

Применение определенного интеграла к задачам в геометрии, механике, физике

Две схемы применения определенного интеграла

Первая схема (схема I) основана на определении определенного ин- теграла, как предела интегральной суммы. Этот прием мы рассмотрели для вычисления массы тонкого неоднородного стержня, работы переменной силы, площади криволинейной трапеции и т. п.

Вторая схема (схема II) основана на том, что по условию задачи со- ставляются соотношения между дифференциалами рассматриваемых ве- личин, а затем интегрируется полученное равенство дифференциалов.

7.10. Вычисление площадей плоских фигур в ДПСК

Решение. Изобразим схематически заданную фигуру (рис. 7.10.1). Разобьем ее прямыми, параллельными оси x , на элементарные части ши-

34

риной dy . Выделим в произвольной точке

c

Замечание 7.10.1. Если плоская фигура ограничена таким обра- зом, что не подчиняется ни первой задаче, ни второй, то фигуру разбивают так, чтобы каждую часть можно было вычислить либо по формуле (7.10.1), либо по формуле (7.10.2).

Пример 7.10.1. Вычислить площадь фи-

гуры, ограниченной линией y 2 = x 3 , прямой y = 1, осью Oy.

Решение. Изобразим фигуру, как на

c

Линия y 2 = x 3 задана неявно, значит нужно выразить одну перемен-

ную через другую. Несложные рассуждения приводят к выводу, что одно- значно выражается переменная x:

2

35

Пример 7.10.2. Вычислить площадь плоской фигуры, ограничен-

ной линиями y = 2 - x , y = x + 4 и осью Ox.

Решение. 1. Изучим кривую y = 2 - x – часть параболы y 2 = 2 - x , у которой ветви направлены в левую часть полуплоскости. Координаты вершины параболы (2, 0).

2. Определим точки пересечения заданных линий. Для этого решим

3. Изобразим схематично заданную фигуру (рис. 7.10.3).

4. Вычислим площадь изображенной фигуры. Поскольку она сверху ограничена двумя различными линиями, придется ее разбивать прямой x = −2 на две части. Будем иметь

Упражнение. Оцените полученный результат, исходя из геомет-

рических соображений. Замените в условии кривую y = 2 - x на кривую y 2 = -x + 2 и вычислите самостоятельно площадь полученной фигуры.

36

7.11. Вычисление площади плоской фигуры, заданной параметрически

Если есть плоская фигура, заданная как в задаче 1 или 2 п. 7.10.1, где ограничивающие кривые заданы параметрически, то применяем теорему о замене переменной в определенном интеграле. Тогда вычисление площади осуществляется по формулам (7.10.1) или (7.10.2) с переходом на новую переменную интегрирования t.

Окончательно,

S = 4S1 = 4 × pab = pab. 4

37

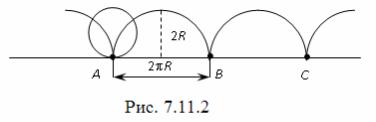
Пример 7.11.2. Вычислить площадь, расположенную под одной аркой циклоиды

Решение. Напомним, что циклоидой называется линия, описываемая точкой окружности, которая катится без скольжения и проворачивания по прямой (рис. 7.11.2).

Из определения следует, что циклоида состоит из ряда арок, причем высота этих арок равна 2R , где R – радиус катящейся окружности, рас- стояния АВ, ВС, … между соседними «точками опоры» равны 2πR .

Вкачестве оси Ox возьмем прямую, по которой катится окружность,

аза начало координат примем положение точки М, описывающей циклои- ду, в тот момент, когда эта точка лежит на оси Ox.

Будем иметь

00

=R 2 2∫π (1 − cost )2dt = 3πR 2.

0

7.12.Вычисление площади криволинейного сектора

вполярной системе координат

Задача 1 . Вычислить площадь криволинейного сектора, т. е. пло-

ской фигуры, ограниченной непрерывной линией ρ = ρ(ϕ) и лучами

ϕ = α, ϕ = β, (α < β) , где ρ и ϕ – полярные координаты.

Решение. Схематично изобразим криволинейный сектор (рис. 7.12.1). Для решения задачи используем схему 2 – « метод дифференциалов»

или «метод отбрасывания бесконечно малых высших порядков».

38

β

О

Рис. 7.12.1

1.Будем рассматривать часть искомой площади S функцией угла j, т. е. S = S (ϕ) , где α ≤ ϕ ≤ β (если ϕ = α, то S (α) = 0 , если ϕ = β, то S (β) = S ).

2.Если текущий полярный угол j получит приращение Δϕ = dϕ , то

соответствующее ему приращение площади S равно площади «элемен- тарного криволинейного сектора» ОАВ. Дифференциал dS представляет собой главную часть приращения S при dϕ → 0 и равен площади круго-

(рис. 7.12.2) относительно полярной оси будем иметь S = 2S1 .

39

Тогда

Решение. Изобразим фигуру, как на рис. 7.12.3.

Найдем сначала площадь половины од-

ного лепестка «розы», т. е. 1 часть всей пло-

Замечание 7.12.1. Если плоская фигура имеет «сложную» форму, то лучами, выходящими из полюса, ее следует разбить на криволинейные сек- торы, к которым применить полученную формулу для нахождения площади.

7.13.Применение определенного интеграла

квычислению пределов (к заданиям на оценку «8» – «9»)

Вычислить пределы:

40