Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

умк_Вакульчик_Опред интеграл

.pdf

Скачиваний:

Добавлен:

18.05.2015

Размер:

3.63 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 2511 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

e	ln 3 x
7) ∫			dx .
	x	2
1

8) ∫arctg x dx .

Ответ: 6e −16 . e

Ответ: π − ln 4 . 4

9) ∫ x 2 sin 2x dx .

	π
	2
10)	∫ x cos x dx .
	0
	e
11)	∫ ln x dx .
	1
	1
12)	∫ x e 2 x dx .
	0
	π
	2
13)	∫ x sin 2x dx .
	0
	2π
14)	∫ x cos 2 x dx .
	0
	π	x
15)	∫ x cos	x	dx .
15)	∫ x cos	2	dx .
	0	2
	0

Уровень 2

Ответ: π − 1 . 8 4

Ответ: π −1. 2

Ответ: 1.

Ответ: e 2 + 1 . 4

Ответ: π . 4

Ответ: π2 .

Ответ: 2π − 4 .

π2

	∫
1)	∫	sin			x dx .	Ответ: 2.
	0
	9					Ответ: 4e3 + 2 .
	9		x
2)	∫e		x	dx .
	0							π
	π							π
	2						e	2 −1
3)	∫ e x cos x dx .					Ответ:			.
3)	∫ e x cos x dx .					Ответ:		2	.
	0							2
	0

101

2	x cos x
4) ∫		dx .

π	sin 2 x
3

3x 2 e x

5)0∫ ( x + 2)2 dx .

1arcsin x

6)∫ x + 1 dx .

7) ∫arctg x dx .

3	x dx
8) ∫		.

π	sin 2 x

9) 1∫ x ln (1 + x 2 )dx .

10) ∫ ln (1 + tg x) dx .

11)∫ cos(ln x) dx .

12) 1∫(arcsin x)2 dx .

3		x sin x
13) ∫			dx .

−	π	cos 2 x
	3

14) ∫sin 2x arctg (sin x) dx .

15) ∫ arctg x −1 dx .

Ответ: ln 3 − π + 2π3 . 2 9

Ответ: e3 + 1. 5

Ответ: π2 − 4 .

Ответ: π −1.

	2
Ответ: π −
			3			π +				1	ln		3		.
						π +					ln				.
4	9			2								2
Ответ: ln 2 −							1		.
Ответ: ln 2 −									.
				2
Ответ: π ln 2 .
	8
		π				−1
	e 2					−1
Ответ:								.
Ответ:								.
	2
Ответ:	π2				− 8
Ответ:				.
	4
2π				− ln tg								5π
Ответ: 2														.
Ответ: 2														.
	3											12

Ответ: π −1. 2

Ответ: 16π − 2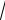3 . 3

102

Домашнее задание

1)Изучить теоретический материал по теме «Несобственные ин- тегралы».

2)Вычислить:

	e3			dx
	∫			dx
а)					.
а)		x			.
	1	x	1 + ln x
	1
	π
	2
	2		cos x − cos 3 x dx .
б)	∫		cos x − cos 3 x dx .

−π

4			dx
в) ∫			dx
						.
	1	+				.
0	1	+		2x + 1
0
2
2		4 − x 2 dx .
г) ∫		4 − x 2 dx .
0
5				dx
д) ∫				dx
							.
	2x		+				.
0	2x		+		3x + 1
0
π

е) ∫ x ln 2 x dx .

π2

ж) ∫ cos 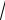x dx .

з) ∫ x 2 e x dx .

Ответ: 2 .

Ответ: 4 . 3

Ответ: 2 − ln 2 .

Ответ: π .

Ответ: 1 ln112 . 5

Ответ: 14 (e 2 −1).

Ответ: – 4.

Ответ: e − 2 .

III.Несобственные интегралы. Сходимость, вычисление

1.В начале занятия выяснить вопросы по выполнению домашнего задания и, в случае необходимости, разобрать решение задачи на доске.

Затем выполнить упражнение:

1	dx	1	x −2dx = −	1	1
∫		= ∫				= −1 −1 = −2 .

−1 x 2		−1		x	−1

103

Ответ неверен, почему? Обратить внимание, что при введении опре- деленного интеграла предполагалось, что выполняются условия: 1) преде- лы интегрирования a и b являются конечными; 2) подынтегральная функ- ция f(x) ограничена на отрезке [a;b] . В этом случае определенный интеграл называется собственным. Если хотя бы одно из указанных условий не вы- полняется, то интеграл называется несобственным.

2. Рассмотреть интегралы с бесконечными пределами (I рода). Пусть функция f(x) непрерывна при x Î[a;+¥) . Тогда несобственный интеграл от

функции f(x) в пределах от а до +∞ определяется равенством:

+∞	f (x)dx = lim	b
∫	f (x)dx = lim	∫ f (x)dx .	(III.1)
a	b→∞	a
a		a

Если предел в правой части равенства (III.1) существует и конечен, то несобственный интеграл называется сходящимся, если же этот предел не существует или бесконечен, то инте- грал называется расходящимся. Гео- метрически несобственный интеграл от неотрицательной функции ( f ( x) ³ 0)

выражает площадь бесконечной криво- линейной трапеции, ограниченной сверху графиком функции y = f ( x) ,

слева – отрезком прямой x = a , снизу – осью Ох (рис. III.1).

В случае сходящегося интеграла эта площадь будет конечной, расхо- дящегося – бесконечной.

Если F(x) – первообразная для f(x), то

	+∞		f (x)dx = lim	b	f (x)dx = lim
		∫	f (x)dx = lim	∫	f (x)dx = lim
		a	b→∞	a	b→∞
		a		a
где	F (+∞) = lim F (b) ;
			b→∞
	b		b
	∫	f (x)dx = lim ∫		f (x)dx = lim
	−∞		a→−∞a		a→−∞
где	F (−∞) = lim F (a) .
			a→−∞

( F (b) - F (a)) = F (+¥) - F (a) , (III.2),

( F (b) - F (a)) = F (b) - F (-¥) , (III.3),

104

Аналогично определяется несобственный интеграл с обоими беско- нечными пределами:

+∞	c	+∞		c	b
∫ f	( x)dx = ∫ f ( x)dx + ∫ f ( x)dx = lim			∫	f ( x)dx + lim ∫ f ( x)dx ,	(III.4)
−∞	−∞	c	a→−∞a		b→+∞ c
где с –	любая точка из интервала (−∞;+∞) .
			+∞
Несобственный		интеграл	∫ f (x)dx		называется сходящимся,	если
			−∞

сходятся оба интеграла в правой части равенства (III.4), или расходящим- ся, если хотя бы один из них не сходится.

Обучающий пример 1. Вычислить несобственные интегралы или установить их расходимость.

+∞ arctg x

а) ∫

dx .

+ x 2

0 1

Решение. Подынтегральная функция

непрерывна

на промежутке

[0;+∞) . Следовательно, по определению

+∞

arctg x

ar ctg

b =

∫

dx = lim

∫ar ctg xd (ar ctg x) = lim

1 + x 2

b→+∞

(arctg 2 b − arctg

0) =

π2

lim

b→+∞ 2

Интеграл сходится.

+∞

б) ∫ cos xdx.

Решение.

+∞

b = lim

(sin b − sin 0) = lim sin b,

∫

cos xdx = lim

∫cos xdx = lim sin x

b→∞

b→+∞

b→∞

b→+∞

т. е. предел не существует. Следовательно, несобственный интеграл рас- ходится.

+∞ 2xdx

в) −∫∞ x 2 + 1 .

Решение. Представим исходный интеграл в виде суммы двух инте- гралов, получим

105

+∞

2xdx

+ 1)

(x + 1)

∫

= ∫

∫

= lim

∫

+ lim

∫

x 2 + 1

−∞ x 2 + 1

a→−∞ a

b→+∞

x 2 + 1

= lim

(ln(x 2 + 1))

0 + lim

(ln(x 2 + 1))

b =

a→−∞

a b→+∞

= −

a→−∞ (

(

))

b→+∞

(

))

= −∞ + ∞.

lim

2 + 1

lim

+ 1

Исходный интеграл расходится, т. к. расходится каждый из интегра- лов в правой части последнего равенства, а достаточно расходимости только одного из них.

+∞ dx

Обучающий пример 2. Исследовать сходимость интеграла a∫ x α .

Решение. По определению

+∞ dx

(

b −α+1 − a −α+1 ).

∫

= lim

∫ x −αdx =

lim

x −α+1

lim

−α + 1

a x α

b→+∞ a

b→+∞

−α + 1

b→+∞

b −α+1

Допустим, что α > 1, тогда

lim

= lim

= 0 , т. к. α −1 > 0 .

α−1

b→+∞

→+∞ b

lim b −α+1

Значит,

при α > 1 интеграл сходится. Пусть α < 1,

тогда

= ¥ ,

+∞ dx

b→+∞

т. е. при α < 1

b dx

интеграл расходится. Если a =

1, то

∫

= lim ∫

dx =

b→+∞ a x

= lim ln

b = lim (ln

- ln

) = +¥ , т. е. расходится.

b→+∞

x × cos x dx .

Обучающий пример 3. Исследовать сходимость

∫

−∞

Решение. По определению

u = x

du = dx

∫ x × cos x dx =

lim

∫ x × cos x dx =

−∞

a→−∞ a

= cos x dx

v = sin x

x ×sin x

== 0 - lim a sin a +1 - lim cos a .

= lim

0 + cos x

a→−∞

Интеграл расходится, т. к.

lim

cos a, lim

sin a

не существуют.

→−∞

Обучающий пример 4 (повышенный уровень). Исследовать, схо-

+∞

дится ли несобственный интеграл

∫

0 (1 + x)6

106

Решение. Преобразуя подынтегральную функцию, получим

+∞

x 2dx

+∞ (x 2 + 2x +1) - 2x -1

( x +1)2 - 2( x +1) +1

∫

= lim

∫

dx =

(1 + x)6

b→+∞ 0

= lim

b d ( x +1)

- 2 lim

b d ( x +1)

+ lim

b d ( x +1)

∫

(1 + x)4

+ x)5

b→+∞

0 (1

→+∞

0 (1 + x)6

= lim

-1

3(1 + x)

4(1

+ x)

5(1

+ x)

b→+∞

= lim

-1

5 +

= =

2(1 + b)

5(1 + b)

b→+∞ 3(1 + b)

3. На доске студенты выполняют задания.

Вычислить:

3.1. ∫

Ответ: – 1.

−∞ x

+∞

3.2. ∫

Ответ:

−∞ x 2 + 4x + 9

4. Рассмотреть признаки сходимости интегралов с бесконечными

пределами:

+∞

10. Пусть для x Î[a;+¥)

0 ≤ f (x) ≤ g(x) . Если ∫

g(x) dx сходится, то

+∞

сходится и

∫ f (x)dx ,

причем

∫

f (x) dx £ ∫

g(x) dx .

Если расходится

+∞∫ f ( x)dx , то расходится +∞∫

g ( x)dx (признак сравнения).

20. Если для

x Î[a;+¥)

f ( x) > 0, g ( x) > 0

и существует конечный

x→∞ g

( x)

∫

предел

lim

( x)

¹ 0 ,

то интегралы

+∞ f

( x)dx

+∞ g

( x)dx

сходятся или

расходятся одновременно (предельный признак сравнения).

+∞			+∞
30. Если ∫	f ( x)	dx сходится, то сходится и	∫ f ( x)dx (последний в

a			a
этом случае называется абсолютно сходящимся).

107

40. Если при x → +∞ функция f (x) > 0

является бесконечно малой,

порядка α по сравнению с

+∞

f (x)dx сходится при a >1 и

, то интеграл ∫

расходится при a <1 или a =1.

Замечание III.1. Как ранее было показано (обучающий пример 2),

+∞ dx

сходится при a >1 и расходится при a <1

или a =1.

интеграл ∫

Обучающий пример 5. Исследовать на сходимость

+∞

1∫

3 + 2x 2 + 5x 4

Решение.

Применив признак сравнения для

x ³1, имеем 3 + 2x 2 + 5x 4 > x 4 ,

откуда

3 + 2x 2 + 5x 4

x 4

+∞

сходится (α = 4 > 1) , то по признаку сравнения схо-

Так как

∫

дится и исходный интеграл.

∞ sin xdx

Обучающий пример 6.

Исследовать на сходимость

∫

x 2

10 и

30. Имеем

f ( x) =

sin x

Решение.

Применим

признаки

x 2

f ( x) =

sin x

≤

sin x

≤

x 2

+∞

сходится (α = 2 > 1) , то, согласно признаку сравнения,

Так как

∫

∞

sin x

dx . Следовательно, на основании признака 30

сходится и интеграл

∫

∞ sin x

сходится интеграл ∫

dx .

Обучающий пример 7. Исследовать на сходимость

∞

− cos

∫ 1

dx .

108

Решение. Подынтегральная функция

f ( x) =1 - cos

= 2sin 2

поло-

жительна и непрерывна при x ³1. Рассмотрим функцию g ( x) =

, инте-

x 2

+∞

сходится (a = 2 >1) , а так как существует предел

грал от которой

∫

f ( x)

2sin

2 1

∞

lim

= lim

= 2 ¹ 0 ,

то

исходный

интеграл

∫ 1 - cos

x→+∞ g ( x)

x→+∞

x 2

также сходится (предельный признак сравнения).

+∞

3 + 2x

Обучающий пример 8. Исследовать на сходимость

∫

dx .

5 x 3 -1

Решение. Подынтегральная функция непрерывна и положительна

при x ³ 2 . Определим порядок ее малости a относительно

при x → +∞

7 x

+ 2

x 7 7

+ 2

3 + 2x

x 2

1 x 2

5 x 3 -1

x 35 5 1 -

5 x

x 5 5 1 -

x 3

при x → +∞ , а a =

<1,

Здесь второй множитель имеет предел

следовательно, данный интеграл расходится.

5. У доски студенты выполняют задание –

исследовать сходимость

интегралов:

∞

а)

∫

Ответ: сходится.

x ( x -1)( x - 2)

∞

(x +

)

x +1

б)

∫

dx .

Ответ: расходится.

1 x 2 + 25 x 4

∞ 1 - 4sin 2x

в) ∫ dx . Ответ: сходится, причем абсолютно.

1 x 3 + 3 x

109

6. Рассмотреть интегралы от неограниченных функций (II рода).

Если функция f ( x)	непрерывна для x [a;b)		и в точке x = b имеет
бесконечный разрыв, то по определению полагают
b∫	f ( x)dx = lim b−ε∫ f ( x)dx .		(III.5)
a	ε→0	a

Если существует конечный предел в правой части формулы (III.5), то несобственный интеграл называется сходящимся; если этот предел не существует или бесконечен, то интеграл называется расходящимся.

Геометрически несобственный интеграл в случае f ( x) > 0 представ-

ляет собой площадь фигуры, ограниченной графиком функции							y = f ( x) ,
прямой x = a и вертикальной асимптотой x = b .
Если функция	f ( x)	непрерывна для x (a;b]				и в точке x = a имеет
бесконечный разрыв, то
	b		b	f ( x)dx .
	∫	f ( x)dx = lim ∫		f ( x)dx .			(III.6)
	a		ε→0a +ε
Если предел в правой части формулы (III.6) существует и конечен, то
несобственный интеграл называется сходящимся.
Если функция	f ( x)	имеет бесконечный разрыв в точке c [a;b] и
непрерывна при x [a ;c) (c;b] , то по определению
b		c−ε1		+ lim	b	f ( x)dx .
∫ f ( x)dx = lim			∫ f ( x)dx	+ lim	∫	f ( x)dx .	(III.7)
a	ε1→0		a	ε 2 →0	c+ε 2
a			a		c+ε 2
Несобственный интеграл			b∫ f ( x)dx	( f (c) = ∞ , a < c < b ) называется
			a

сходящимся, если оба предела в правой части равенства (III.7) существуют и конечны.

Признаки сходимости несобственных интегралов второго рода по формулировке совпадают с признаками сходимости несобственных инте- гралов первого рода, только сравнение идет с эталонами в окрестности то- чек разрыва. В качестве интегралов-эталонов выступают интегралы вида

b	dx		, которые при m <1,	Н.И.	сходятся	, где c [a;b] .
∫

a	x − c	m	m ³1,	Н.И.	расходятся

110

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 2511 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в папке Высшая математика (РТФ)

#
18.05.20152.77 Mб51умк_Вакульчик_Неопределенный интеграл.pdf
#
18.05.20153.63 Mб42умк_Вакульчик_Опред интеграл.pdf
#
18.05.20154.76 Mб40умк_Вакульчик_Элементы векторной алгебры.pdf
#
18.05.20155.38 Mб46умк_Вакульчик_Элементы линейной алгебры.pdf
#
18.05.20151.33 Mб47умк_Мальцев_Осн дискретной матем.pdf
#
18.05.20153.75 Mб53умк_Пальчик_Теория вероятностей.pdf
#
18.05.20155.68 Mб35умк_Цывис_Диф.уравнения_Ряды.pdf