Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

умк_Вакульчик_Опред интеграл

.pdf

Скачиваний:

Добавлен:

18.05.2015

Размер:

3.63 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 2510 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

нений

= sin t

= sin t ; можно принять t

= π

и t

= π , но можно так

же

выбрать и

другие значения, например,

5π

и t

2π

x = sin t

В обоих случаях переменная

пробегает

весь

отрезок

;

причем

функция

sin t

монотонна

на

отрезке

Рис. II.1

2π

5π

;

, и на отрезке

;

(рис. II.1).

Покажем, что результаты интегрирования совпадают. В самом деле,

2 +

costdt

3 = ln tg

∫

= ∫

= ln | tg

− ln tg

= ln

1 − x 2

π sin t cos t

π sin t

С другой стороны, учитывая, что на отрезке

2π

;

5π

функция cos t

принимает отрицательные значения, получим

2π

5π

2 +

costdt

∫

= ∫

= ln

2π

1 x

1 − x 2

5π sin t (− cost )

2π sin t

Замечание II.2. Следует подчеркнуть, что нельзя брать t

5π

t 2 =

5π

значение функции x = sin t

т. к. при изменении t на отрезке

;

выходит за пределы отрезка

;

Обучающий пример 5 (повышенный уровень). Вычислить

x sin x

I = ∫

dx .

0 1 + cos 2 x

Решение. Представим этот интеграл в виде суммы двух интегралов:

2	x sin x	π	x sin x
I = ∫		dx + ∫		dx = I1 + I 2 .
	1 + cos 2 x		1 + cos 2 x
0		π
		2

π	x sin x
К интегралу I 2 = ∫	x sin x	dx применим подстановку x = π − t .
К интегралу I 2 = ∫	1 + cos 2 x	dx применим подстановку x = π − t .
π	1 + cos 2 x
2

π			x =	π − t, dx = −dt						(π − t )sin (π − t )

	x sin x				π		π		0
I 2 = ∫		dx =	x =			t =		,	= ∫	1 + cos 2 (π − t )	dt =
				2			2
π	1 + cos 2 x		x =						π
2				π		t = 0.			2

(π − t )sin t

sin t

t sin t

= ∫

dt = π∫

dt −

∫

1 + cos 2 t

+ cos 2 t

1 + cos 2 t .

Следовательно,

x sin xdx

sin tdt

t sin tdt

I = I1 + I 2 = ∫

+ π∫

− ∫

1 + cos 2 x

+ cos 2 t

1 + cos 2 t

Так как первый и третий интегралы отличаются только обозначе-

ниями переменной интегрирования, то

cos t = z, − sin t = dz

sin t dt

I = π∫

t = 0 z = 1,

= −π∫

1 + cos 2 t

1 + z

1 + u

t = π z = 0.

Замечание II.3. Неопределенный интеграл ∫

x sin x

не выра-

+ cos 2 x

жается в элементарных функциях. Однако данный определенный интеграл вычисляется, если прибегнуть к искусственному приему, который пред- ставлен выше.

Обучающий пример 6 (повышенный уровень). Доказать, что все-

гда можно подобрать линейную подстановку x = kt + c (k, c – постоянные) так, чтобы любой данный интеграл с конечными пределами a и b преобра- зовать в интеграл с пределами 0 и 1.

Решение. Прежде всего отметим, что подстановка x = kt + c удовле- творяет условиям теоремы о замене переменной. Так как при х = а должно быть t = 0 и при x = b должно быть t = 1, то для определения величин k и c имеем систему уравнений:

a = k × 0 + c		c = a, k = b - a .
	+ c
b = k ×1

Следовательно,

b∫ f ( x)dx = (b - a)1∫ f ((b - a)t + a)dt .

Обучающий пример 7 (повышенный уровень). Доказать, что ин-

π sin 2kx

теграл ∫

dx при целом k

равен 0.

sin x

Решение.

π sin 2kx

x = p - t, dx = -dt

0 sin 2k (p - t )

π sin 2kt

∫

dx =

x = 0 t = p,

= -∫

dt = -∫

dt = -I .

sin (p - t )

sin x

x = p t = 0.

sin t

Так как определенный интеграл не зависит от обозначения перемен-

ных интегрирования, то I = −I , откуда I = 0 .

Обучающий пример 8 (повышенный уровень).

Вычислить инте-

5π

sin 2x

грал

∫

dx .

π cos

4 x + sin 4 x

Решение. Подынтегральная функция является периодической функ-

цией с периодом π , т. к.

f ( x + p) =

sin 2( x + p)

sin 2x

= f ( x) .

cos 4 ( x + p) + sin 4 ( x + p)

cos 4 x + sin 4 x

Поэтому можно от верхнего и нижнего пределов интегрирования от- нять число π .

5π

∫

	π		π
sin 2x	4	sin 2x	4	tg xdx
	dx = ∫		dx = 2 ∫		=
cos 4 x + sin 4 x		4 x + sin 4 x		2 x (1 + tg 4 x)
	0 cos		0 cos

tg x = t,

= dt

cos 2 x

2tdt

x = 0 t = 0,

= ∫

= arctg t

1 + t 4

x =

t = 1.

Обучающий пример 9. Решить уравнение ∫

ln 2

e x −1 6

Решение. Вычислим интеграл в левой части

e x −1 = t e x = t 2 + 1

x = ln (t

+ 1), dx =

2tdt

∫

1 + t

ln 2 e x −1

x = ln 2 t = 1

x = x

t = e x −1

	e x −1
	e x −1	dt			x
=	∫	dt	= 2arctg t	e −1 =

		1 + t 2
	1	1 + t 2		1

= 2arctg		− 2arctg1 = 2arctg		− 2 π = 2arctg		− π .
	e x −1		e x −1		e x −1
4					2

Имеем уравнение

2arctg e x −1 − π = π ; 2 6

2arctg e x −1 = 2π ; 3

arctg e x −1 = π ; 3

e x −1 = tg π ; 3

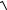
e x −1 = 3 ; e x −1 = 3;

e x = 4 ; x = ln 4 .

3. Выполнить (самостоятельно каждому свой вариант, два студента у доски выполняют свои задания из 1-го и 2-го уровня).

Уровень 1

	8	xdx
1)			.
	∫
		1 + x
	3
	1	dx

2)					.
	0∫ x
		2 + 4x + 5
	1	dx
3)	∫			.


	0	4 − x 2

1 dx

4)0∫ e x + e − x .

	16		dx
	∫		dx
5)				.
5)				.
		x + 4 x
	1
	1		xdx
6)	∫		xdx		.
6)	∫				.
	−		5 − 4x
	1

7dx

7)−∫11 + 3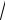 x + 1 .

8)∫sin 3 xdx .

	0
	3,5	dx
	∫	dx
9)			.


	2	5 + 4x − x 2

2dx

10)1∫ x 2 + 2x .

1dx

11)−∫2 x 2 + 4x + 13 .

12)∫ x 42x −1dx .

13)∫ x 2 9 − x 2 dx .

Ответ: 32 . 3

Ответ: arctg 3 − arctg 2 .

Ответ: π . 6

Ответ: arctg e − π . 4

Ответ: 4 ln 9 . 3 2

Ответ: 1 . 6

Ответ: 3ln 3 .

Ответ: 2 . 3

Ответ: π . 6

Ответ: 1 ln 3 . 2 2

Ответ: π . 12

Ответ: 14 . 45

Ответ: 81 π . 16

	9	xdx
14)	∫	xdx	.
14)	∫		.
	1	2x + 7
	1
15)	∫3 x (3 − x)7 dx .
	2

1) Можно ли интеграл

становки x = 2cost ?

Ответ: 28 . 3

Ответ: 19 . 27

Уровень 2

∫2x 3 4 − x 2 dx вычислить с помощью под-

Ответ: нет.

2) Можно ли интеграл ∫ x 2 + 1dx вычислить с помощью подста-

																1
															3
новки x =					1				?									Ответ: нет.
новки x =									?									Ответ: нет.
			sin t
															2
															2
3)						Можно ли интеграл ∫ 3 1 − x 2 dx вычислить с помощью подста-
															0
новки x = cos t ?																		Ответ: нет.
	1				x 2 dx												1
4)	∫												.					Ответ:			.
4)	∫							1)					.					Ответ:			.
	0 ( x +							1)			4						24
Указание.															x + 1 = t .
	ln 2																		4 − π
	ln 2						e x −1 dx .
5)	∫																	Ответ:						.
5)	∫																	Ответ:						.
	0																2
	0
Указание.															e x −1 = t 2 .
										3
	7							x		3	dx
	∫							x			dx
6)														.				Ответ: 3 .
6)														.				Ответ: 3 .
				3 (x 2 + 1)2
		3		3 (x 2 + 1)2
Указание.															x 2 + 1 = t .
	3																		81π
	3									9 − x 2 dx .
7)	∫ x 2																	Ответ:				.
7)	∫ x 2																	Ответ:				.
	−3																8
	−3
	1					t dt												Ответ: −		17
8) ∫						t dt						.								17			.
8) ∫												.											.
	5					5 + 4t											6
	5

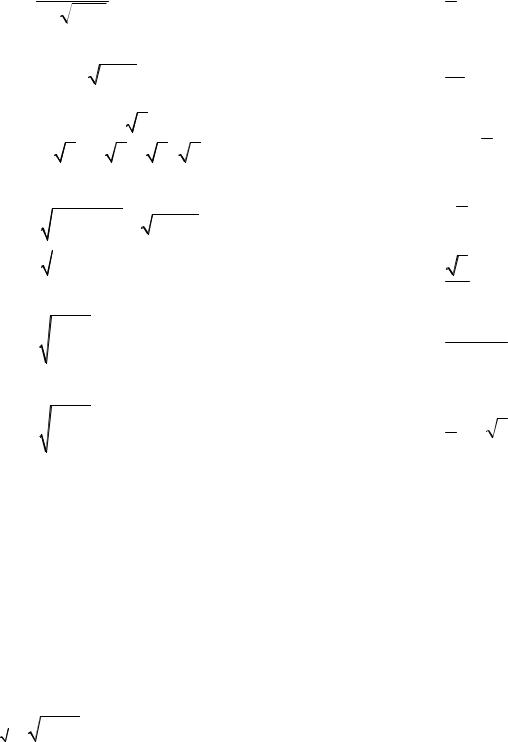
0dx

9)−∫11 + 3 x + 1 .

	2		3 x
10)	∫sin		3 x				cos x dx .
	0
	64						2 +			3
	64						2 +			3	x
11)	∫														dx .
11)	∫														dx .
	1 (6 x + 23 x + x ) x
	4					( x −1)dx
12)	∫					( x −1)dx										.


		(3x − 4)2 − 3
	1 3												+ 1
	1 3											3x − 4	+ 1

	6	x	2		− 9
13)	∫	x			− 9			dx .
13)	∫	x 4						dx .
	3	x 4
	3
	3			x
14)	∫			x		dx .

		6
	0	6		− x
	0
Указание.											x = 6sin 2 t .
	1
	1			x
15)	∫			x		dx .

		4
	0	4		− x
	0
Указание.											x = 4sin 2 t .
															Уровень 3
1) Вычислить									50∫	f ( z ) dz :					1∫ f (50z ) dz .
									0					0

Ответ: 3 (ln 4 −1) . 2

Ответ: 8 . 21

Ответ: 30ln 3 − 6 . 2

Ответ: 2 1 . 4

Ответ: 3 . 72

Ответ: 3(π − 2) . 2

Ответ: 2 π − 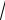3 . 3

Ответ: 50.

Указание. В первом интеграле перейти к пределам интегрирования от 0 до 1, используя формулу x = kt + c из обучающего примера 5.

2) Решить уравнение:

Ответ: x = 2 .

∫

t 2 −1 12

3) Вычислить сумму интегралов

−5

2 2

( x+5)

9 x−

∫ e

dx + 3∫e

3 dx .

Ответ: 0.

−4

Указание. Преобразуйте каждый из интегралов в интеграл с преде-

лами от 0 до 1. Заметим, что каждый из интегралов ∫e( x+5)2 dx и

	2	2
9 x−
9 x−	3
∫e	3

dx в отдельности не берется в элементарных функциях.

1 ln (1 + x)							π
4) ∫		dx .					Ответ: ln 2 .

0 1 + x 2						8
Указание.	а) примените подстановку				x = tg t ;
				sin t + π
			2
б) преобразуйте сумму 1 + tg t =					4		;

cost
π	π − z .
4
в) к интегралу ∫ ln cost dt примените подстановку t =
0	4
0

Этот пример, как и предыдущий, интересен тем, что неопределенный

ln (1 + x)

интеграл ∫ 1 + x 2 dx не выражается в элементарных функциях.

4. Отметить, что если для нахождения первообразной применяется метод подстановки, то можно в полученной первообразной не возвращать- ся к прежней переменной, но тогда обязательно надо определить пределы интегрирования новой переменной.

Однако при возникновении затруднений с определением пределов интегрирования новой переменной, можно первообразную выразить через исходную переменную, а затем применить формулу Ньютона – Лейбница с пределами интегрирования.

Например: ∫

x = t 2 ,t =

2tdt

= 2∫

tdt

∫

= ∫

= 2∫

=2ln

t + 1

+ C =

(

t +

x + x

dx = 2tdt

+ t

)

= 2ln x + 1 + C .

4	dx		= 2	( ln		+ 1	)	4 = 2(ln		+ 1	− ln		+ 1	) = 2ln	3
∫																.
					x				4			1
	x +
1		x						1						2

5. Сформулировать теорему интегрирования по частям в опреде-


ленном интеграле: если функции u = u ( x)			и v = v ( x) имеют непрерывные
производные на отрезке [a;b] , то имеет место формула

	b		b
	∫u dv = u v	ba − ∫v du		.


	a		a

Заметить, что формулу Ньютона – Лейбница можно применять к ка- ждому слагаемому в отдельности, не дожидаясь нахождения всей первооб- разной.

Обучающий пример 10. Вычислить ∫e ( x + 1)ln x dx .

Решение. Применим формулу интегрирования по частям.

∫e ( x + 1)ln x dx

e	x 2		dx
−∫			+ x
		2		x

1

ln x = u

dx = du

( x + 1)dx = dv v = ∫( x + 1)dx =

+ x ln x

−

+ x

e 2

x 2

e 2

e 2 + 5

+ e −

0 −

+ x

+ e −

− e +

+ 1

Обучающий пример 11. Вычислить

J = ∫ e ax sin bx dx .

u = sin bx du = b cosbx dx

b −

Решение. J = ∫ e ax sin bx dx =

e ax sin bx

e axdx = dv v =

e ax

−

∫ e ax cosbx dx = −

J1 .

Применим теперь формулу интегрирования по частям к интегралу J1 .

u = cosbx

du = −bsin bxdx

b +

J1 = ∫ e ax cosbx dx =

e ax cosbx

dx = dv

v =

π aπ

b b

e b

∫ e ax sin bx dx = −

−

J .

a 0

aπ

−

b 2

Тогда

J = −

1 =

be b

J .

a 2

aπ

b e

+ 1

b e

+ 1

a 2 + b

Отсюда

J +

J =

aπ

+ 1

J =

a 2 + b 2

В частности, при a = b = 1 получаем

∫e x sin x dx = 12 (e π + 1).

6.Выполнить (самостоятельно, каждому свой вариант, два студента

удоски выполняют свои задания).

Уровень 1

e−1

1)∫ ln ( x + 1)dx .

	1	− x dx .
2)	∫ x e	− x dx .
	0
	2
3)	∫ x ln x dx .
	1
	π
4)	∫ x sin x dx .
	0
	0		− x dx .
5)	∫ x e		− x dx .
	−1

6) 2∫ln (x 2 + 4)dx .

Ответ: 1.

Ответ: 1 − 2 . e

Ответ: 2ln 2 − 3 . 4

Ответ: π .

Ответ: – 1.

Ответ: π − 4 + 6ln 2 .

100

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 2510 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в папке Высшая математика (РТФ)

#
18.05.20152.77 Mб51умк_Вакульчик_Неопределенный интеграл.pdf
#
18.05.20153.63 Mб42умк_Вакульчик_Опред интеграл.pdf
#
18.05.20154.76 Mб40умк_Вакульчик_Элементы векторной алгебры.pdf
#
18.05.20155.38 Mб46умк_Вакульчик_Элементы линейной алгебры.pdf
#
18.05.20151.33 Mб47умк_Мальцев_Осн дискретной матем.pdf
#
18.05.20153.75 Mб53умк_Пальчик_Теория вероятностей.pdf
#
18.05.20155.68 Mб35умк_Цывис_Диф.уравнения_Ряды.pdf