14-es_1 / Высшая математика (РТФ) / умк_Вакульчик_Опред интеграл
.pdf
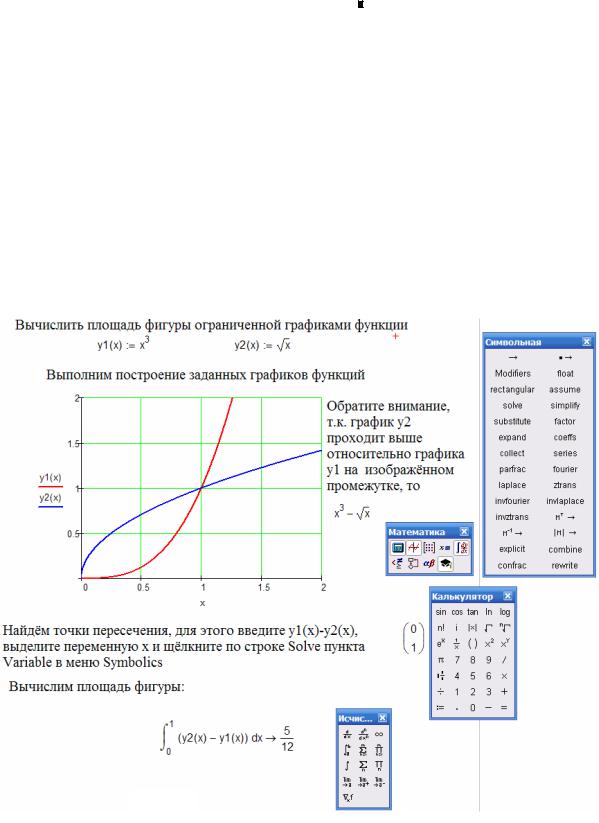
Рис. П.1
Отметим, что, используя математический пакет Maple, Вы можете произвести вычисление несобственного интеграла, как в представленном примере (рис. П.2).
Рис. П.2
162


Рис. П.4 |
Рис. П.5 |
Рис. П.6 |
Появится символ интеграла с несколькими место заполнителями, в которые нужно ввести нижний и верхний пределы интегрирования, подынтеграль- ную функцию и переменную интегрирова- ния. После этого выберите панель кальку- лятора и с ее помощью введите подынте- гральную функцию (рис. П.7).
Символ интеграла Вы можете вы- звать и другим способом: щелкните в сво- бодном месте и наберите знак &.
Обратите внимание на то, что опера- тор определенного интеграла содержит че- тыре маркера, которые следует заполнить в
Рис. П.7 соответствии с математической формулой. Чтобы получить результат интегрирования,
⌠ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
следует ввести знак равенства или символьного равенства: ⌡ |
|
|
|
|
|
d |
|
. |
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
Например, определенный интеграл x ×ln( x) от 0 до 1 может быть вы- числен следующим образом:
1. После появления символа интеграла щелкните на поле внизу и наберите 0. Щелкните на верхнем поле и нажмите клавишу 1. Так задаются верхний и нижний пределы интегрирования.
⌠1
 d
d
⌡0
164