Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

умк_Вакульчик_Опред интеграл

.pdf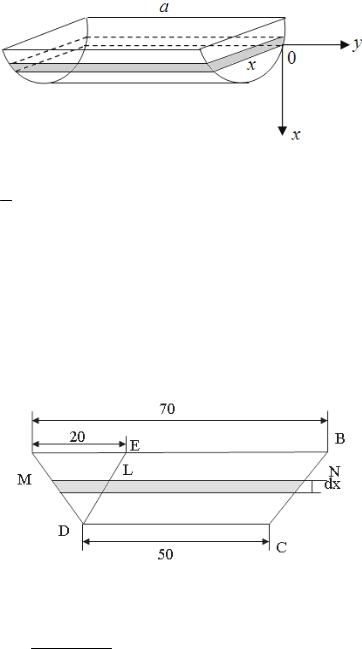

Скачиваний:

Добавлен:

18.05.2015

Размер:

3.63 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1516 / 2516 17 18 19 20 21 22 23 24 25 > Следующая >>>

3. На доске одновременно три студента решают задачи. Студент с помощью преподавателя и аудитории решает задачу 3.1. Студенты творче- ского уровня обучения задачи 3.2 и 3.3 решают самостоятельно. Решение этих задач обсуждается после решения задачи 3.1.

3.1. Найти работу, затраченную на выкачивание воды из корыта, имеющего форму полуцилиндра, длина которого а, радиус r (рис. VI.10).

Рис. VI.10

Ответ: 2 γgar 3 . 3

3.2. Найти давление бензина, находящегося в цилиндрическом ба- ке высотой h = 3,5 м и радиусом основания r = 1,5 м, на его стенки, если

γ = 900кг/м3.

Ответ: 161700 π (Н).

3.3. Вертикальная плотина имеет форму трапеции, верхнее основа- ние которой равно а = 70м, нижнее b = 50м, а высота h = 20м. Найти силу давления воды на плотину (рис. VI.11).

Рис. VI.11

Ответ: P = (a + 2b)h 2 ≈ 110853000 (H ) . 6

4. Преподаватель у доски решает следующие задачи:

4.1. (повышенный уровень). Какую работу затрачивает подъемный кран при извлечении железобетонной надолбы со дна реки глубиной 5 м,

151

Если надолба имеет форму правильного тетраэдра с ребром 1 м, а плот- ность железобетона 2500 кг/м3 (рис. VI.12).

Рис. VI.12

Решение. Высота тетраэдра h =							6			м, объем тетраэдра V =			2	м3. Вес
Решение. Высота тетраэдра h =							3			м, объем тетраэдра V =			12	м3. Вес
							3						12
надолбы в воде
P =		1			× 2500 ×9,8 -	1			×1000 ×9,8 =1225			(Н),
		1		2		1		2			2
				2				2			2
1	12		12
	12		12

поэтому работа на извлечение надолбы до момента появления на поверх- ности воды ее вершины составляет


			6

A =1225	2 (5 - h) =1225 2 5	-		» 7247,5 (Дж).
A =1225	2 (5 - h) =1225 2 5	-		» 7247,5 (Дж).
1			3
			3

Теперь найдем работу А2 на извлечение надолбы из воды. Пусть вершина тетраэдра вышла на высоту (5 + y), тогда объем малого тетраэдра,

вышедшего из воды			3	y 3	, а вес тетраэдра
вышедшего из воды		8			, а вес тетраэдра
		8
P =	2500 ×9,8						-	1			-	1	y 3		×1000 ×9,8(Н).
	2500 ×9,8					2		1		2		1		3
						2				2				3
2		12							8
		12						12	8

Следовательно,

									6
h	24500		9800		9800				3
h	24500		9800		9800	y 3			3	(1225 2	+12253 3y 3 )dy =
A2 = ∫		2 -		2 +			3	dy = ∫
A2 = ∫	12	2 -	12	2 +	8		3	dy = ∫
0	12		12		8				0

152

	1225		4			6

= 1225 2 y +		3y			3 ≈ 1650, 26 (Дж).
	4
				0

Тогда A = A1 + A2 = 7247,5 + 1650,26 = 8897,76 (Дж).
4.2. Вычислить координаты центра тяже-			y
сти однородной плоской фигуры, ограниченной			y
сти однородной плоской фигуры, ограниченной
линиями y = 6 − x 2 , y = 2 .
Решение. Изобразим фигуру на рис. VI.13.			2
Решение. Изобразим фигуру на рис. VI.13.			2
Указание. Из однородности	и симмет-			x
ричности данной фигуры следует,	что xc = 0 .
		-2 0 2


Для определения yc = 0 воспользуйтесь фор-
мулой VI.15.
Ответ: xc = 0, yc = 3,6 .		Рис. VI.13

Домашнее задание

1.Решить задачи.

а) Скорость тела меняется по закону v = 0, 03t 2 м/с. Какой путь прой- дет тело за 10 с? Чему равна средняя скорость движения?

Ответ: 10 м, 1 м/с.

б) Какую работу затрачивает подъемный кран при извлечении мед- ного конуса из морской воды? Конус с вертикальной осью погружен в воду так, что его вершина находится на поверхности воды. Высота кону- са H = 1 м, радиус основания R = 1 м, плотность меди γ1 = 8900 кг/м3, а морской воды γ2 = 1020кг/м3 .

1	πR 2 H	2	γ1	−	3	γ		≈ 8519π(Дж) .
Ответ:							2
					4
3

2. Выполнить задания из внеаудиторной контрольной работы.

VII. Решение нулевого варианта

из внеаудиторной контрольной работы

1. Вычислить с точностью до двух знаков после запятой:

3	x2dx
а) ∫		.
	6
1	1 + x

153

Решение. Для вычисления первообразной подынтегральной функции воспользуемся методом подведения под знак дифференциала, получим

3	x 2dx		1	3	dx3		1				=	1
		=				=			3 \|	3			(arctg 3		- arctg1) = 0, 20 .
								arctg x						3

1∫ 1+ x 6 3 1∫ 1+ (x3 ) 2							3		1	3

Ответ: 0,20.

б) ∫ xe −2xdx .

Решение. Применим формулу интегрирования по частям

∫udv = uv -∫vdu . Тогда

1									u = x,				du = dx,																		1			1
2		−2x							u = x,				du = dx,													1			−2x		1		2				1		−2x
∫		−2x																								1			−2x				2				1		−2x
	xe			dx =					dv = e				−2x		dx, v = -				1		−2x		= -				xe				2		+∫					e		dx =
	xe			dx =									−2x						1	e	−2x		= -			2	xe				2		+∫				2	e		dx =
0																			2	e						2					0		0				2
0																																	0


			1			1		1			1			1							1			1			1			1					1
															)e −2 x	1
																		= -				-			+			= -				+				= 0, 07 .
	= -				×		×			+		×(-					2
	= -				×		×			+		×(-					2
			2 2 e 2										2			0					4e 4e 4									2e 4
																0

Ответ: 0,07.

2. Вычислить несобственные интегралы или доказать их расходимость.

0		dx
а) ∫		dx	.
а) ∫			.
−	3	4x + 3
	3

4

Решение. Подынтегральная функция имеет точку разрыва второго

рода при x = - 3 . Таким образом, имеем несобственный интеграл от неог-

раниченной функции, вычислим его по определению:

0			dx						0					dx						1		0				d (4x + 3)
∫			dx			= lim				∫				dx				= lim		1				∫		d (4x + 3)				=
∫						= lim				∫								= lim						∫						=
−	3		4x + 3				ε→0		−	3	+ε			4x +		3 ε→0 4						−		3	+ε		4x + 3
	3									3														3

4									4													4
													0

		=		2											=		1		lim (				+ 4e) =					3	.

					lim			4x + 3					3								3
					lim			4x + 3					3								3
		4			ε→0							-		+ e			2 ε→0									2
		4			ε→0							-	4	+ e			2 ε→0									2
													4

Ответ: интеграл сходится.

∞

б) −∞∫ x 2 + 2x + 2

154

Решение. Заданный интеграл является интегралом по бесконечному промежутку. Для его вычисления разобьем отрезок интегрирования на два промежутка и воспользуемся определениями Н.И. первого рода:

∞

∫

= ∫

∫

+ 2x + 2

2x + 2

−∞

2x + 2

+ lim

lim

∫

+ 2x +

A→−∞ A x

B→∞

x 2 + 2x + 2

+ lim

lim

∫

+ 1) 2 +

A→−∞ A (x + 1) 2 + 1

B→∞

x + 1 = t, x = t −1, dx = dt,

α 1 = A + 1, β1 = 1, α 2 = 1,

B+1

β2

= B + 1

= lim

∫

+ lim

∫

t 2 + 1

A→−∞ A+1 t

→∞

B + 1

lim

(arctg t

) + lim (arctg t

)

A→−∞

+ 1

B→∞

= lim ( π − arctg A + 1) +

lim (arctg B + 1 − π) =

π + π + π − π = π .

A→−∞

B→∞

2 4

Ответ:

интеграл сходится.

3. Вычислить (с точностью до двух знаков после запятой) площадь

фигуры, ограниченной указанными линиями:

y2 = 9x, y = 3x . Построить

схематически фигуру.

Решение. Изобразим фигуру, ограниченную

линиями: y2 = 9x , y = 3x (рис. VII.1).

Найдем пределы интегрирования, для этого

решим уравнение

9x = 9x2 9x − 9x2 = 0 9x(1 − x) = 0 .

Отсюда будем иметь x = 0 или x = 1.

Вычислим площадь фигуры. Для этого вос-

S =

( x)

− y ( x) dx .

пользуемся формулой

∫

Рис. VII.1

Будем иметь

S = 1

− 3x)dx = 31

1 −

1) = 3(

(

xdx = 3(

−

) =

xdx − 3

∫

Ответ:

1/2.

155

4. Вычислить (с точностью до двух знаков после запятой) объем те- ла, полученного вращением фигуры

			3	t вокруг оси Oy. Сделать схе-

	F : x = 7cos
	y = 7sin3 t,
	матический рисунок.
		Решение. Изобразим схематически за-
	данную фигуру – астроиду (рис. VII.2).
		Для нахождения объема полученной
	фигуры воспользуемся следующей формулой:
		t1`		2 dy . В нашем случае имеем
Рис. VII.2	V y = p ∫ (x(t))
		t2

( x (t )) 2

Значит,

=49cos 6 t , dy = 7 ×3sin 2 t × costdt = 21sin 2 t × costdt ,

x= 0, t = p/2; x = 7, t = 0.

2																			2
V y = -2p∫ 49cos 6 t × 21×sin 2 t × costdt																	= -2058p∫ (1 - sin 2 t)3 sin 2 td (sin t) =
0																			0
	π
= -2058p	2		- 3sin 2 t + 3sin 4 t - sin 6 t)sin 2 td (sin t) =
= -2058p	∫ (1		- 3sin 2 t + 3sin 4 t - sin 6 t)sin 2 td (sin t) =
	0
	π
	2
= -2058p∫ (sin 2 t - 3sin 4 t																	+ 3sin 6 t - sin 8 t)d (sin t) =
π	0					π													π										π
π						π													π										π
2						2													2									2
= -2058p( ∫ (sin 2 td (sin t) - 3						∫ (sin 4 td (sin t) + 3∫ (sin 6 td (sin t) -																							∫ (sin	8 td (sin t)) =
0						0													0									0
	sin		3		t			p				3		sin 5 t				p	3	sin 7 t		p			sin	9	t		p


= -2058p(							2			-								2 +				2	-						2 ) =
= -2058p(							2			-								2 +	7			2	-						2 ) =
	3						0			5								0	7			0	9						0
							0											0				0							0
= -2058p(-		1		+				3	-		3		+		1	) = -2058p(-					16			) » 328,40 .
= -2058p(-				+					-				+			) = -2058p(-					315			) » 328,40 .
	3					5				7				9							315
Ответ: 328,40	ед3 .

156

5. Вычислить силу давления воды на вертикальную треугольную пластину (треугольник равнобедренный) с основанием 2 м, высотой Н = 1 м, опущенную в воду вершиной вниз так, что основание находиться на по- верхности воды (γ = 9,81 кН/м3). Изобразить графически.

Решение. Изобразим схематически пластину (рис. VII.3). Рассмотрим горизонтальную полоску на произвольной глубине x,

имеющую толщину, равную dx. Для удобства рассуждений рассмотрим еще один схематический чертеж (рис. VII.4). Так как dx достаточно мало, то, приближенно принимая эту полоску за прямоугольник, находим диф- ференциал площади dS = MN × dx . Выразим ширину элемента разбиения MN через x и данные задачи.

				Рис. VII.3	Рис. VII.4
	Из			подобия треугольников DBMN и	DABC	получаем
MN	=	x	,	MN = 2x , тогда dS = 2xdx . Вычислим элементарную силу дав-
2	=		,	MN = 2x , тогда dS = 2xdx . Вычислим элементарную силу дав-
2	1

ления воды на эту полоску, воспользуемся при этом формулой P = gShg .

Будем иметь dP = ggdS × x = gg × 2xdx × x . Тогда

1	x		3	1		2		2		2
1			3

P = 2gg ∫ x	2dx = 2gg			0	=		gg . Отсюда P =		gg =		9,812	= 64,16 .
P = 2gg ∫ x	2dx = 2gg	3			=	3	gg . Отсюда P =	3	gg =	3	9,812	= 64,16 .
		3				3		3		3
0
0

Ответ: 64,16 Н.

6. Найти координаты центра масс однородной плоской фигуры, ограниченной линиями y = x +1 , y = 0, x = 0 . Построить схематически чертеж.

Решение. По условию задачи изобразим схе-

Рис. VII.5

матически заданную фигуру – рис. VII.5.

Массу пластины найдем из формулы m = b∫g[ f1(x) - f 2 (x)]dx . Подставляя

				a
данные задачи, будем иметь
0		0						2	0		2

						3
m = ∫ g(	x +1 - 0)dx = g ∫		x +1d (x +1) = g		(x +1)	3	×			= g		.
m = ∫ g(	x +1 - 0)dx = g ∫		x +1d (x +1) = g		(x +1)		×	3	-1	= g	3	.
−1		−1						3	-1		3
−1		−1

157

∫γx[ f1(x) − f 2 (x)]dx

Формула координаты x центра масс имеет вид x

В нашем случае

u = x, du = dx

0 -

xc =

∫ x

dx =

dv =

= x

(x +1)3

∫

(x +1)3

dx =

x +1

−1

-1

−1

v =

(x +1)3

0 = -

= -

(x +1)5

-1 5

Формула координаты у центра масс имеет вид

b∫g[ f1(x) + f 2 (x)]×[ f1(x) - f 2 (x)]dx

yc =

			3	0												3	0							3		0	0
	=			∫						×			dx =					∫		(x +1)dx =						( ∫ xdx + ∫
Тогда yc						x +1						x +1
Тогда yc			4			x +1						x +1
			4	−1										4				−1						4 −1			−1
				=			3	(	x2		0 + x				0 ) =			3	(-		1	+1) =	3		.
							3		x2									3			1		3

					4 2						-1				-1		4			2		8
		-	2	3
Ответ:				;	.
Ответ:				;	.
			5	8

7. Найти длину кривой, заданной уравнениями y = ln sin x

dx) =

( p £ x £ p) . 3 2

																b
																b		1 + ( y¢) 2 dx . Вы-
Решение. Длину кривой найдем из формулы															l = ∫			1 + ( y¢) 2 dx . Вы-
																a
числим y¢ = (ln sin x)¢ =			1	cos x = ctg x . Отсюда будем иметь
числим y¢ = (ln sin x)¢ =			sin x	cos x = ctg x . Отсюда будем иметь
			sin x
π				π						π											p
π				π						π											p
2				2		1				2	1						x				2
2				2						2
l = ∫	1 + ctg 2 xdx = ∫								dx = ∫				dx	= ln(tg					)				=
l = ∫	1 + ctg 2 xdx = ∫				sin 2 x				dx = ∫				dx	= ln(tg					)		p		=
π				π	sin 2 x					π sin x								2			p
3				3						3											3
= ln(tg p) - ln(tg p) = ln1 - ln
							3	= -ln			3	= -ln		1		= ln						=		1	ln 3.
							3				3			1						3				1
																				3
4	6					3				3				3									2
Ответ:	1	ln 3 .
Ответ:		ln 3 .
	2

158

8. Найти неопределенные интегралы:

а) ∫

dx .

+ 3x

Решение. Воспользуемся методом подведения под знак дифферен-

циала, получим: ∫

∫

d (3x3 +1)

dx =

ln(1

+ 3x

) + C .

+ 3x

1 + 3x

б) ∫arcsin 2xdx .

Решение. Воспользуемся формулой интегрирования по частям

∫udv = uv -∫vdu . Для заданного интеграла будем иметь

u = arcsin 2x, du =

2dx

x × 2dx

∫arcsin 2xdx =

= x × arcsin 2 x - ∫

1 - 4x2

dv = du,

v = x

1 - 4 x 2

∫

d (1 - 4x2

)

= x × arcsin 2x +

1 - 4x2

+ C .

1 - 4x2

в) ∫cos2 3xdx .

Решение. В подынтегральном выражении понизим степень, получим

∫cos2 3xdx = ∫

1 + cos 6x

dx =

∫dx +

∫cos 6xd 6x =

x +

sin 6x + C .

г) ∫

+ 23

dx .

(x +1)(x

+ 6x +13)

Решение. Разложим подынтегральную функцию на простейшие дроби:

x2 + 23

Bx + C

(D = – 16 < 0).

x +

2 + 6x +13

(x +1)(x2 + 6x +13)

1 x

Определим

произвольные

постоянные.

Составим

уравнение

x2 + 23 = A(x2 + 6x +13) + (Bx + C)(x +1) .

Отсюда,

придавая

переменной

значения x = −1,

x = 0 и приравнивая коэффициенты при x2 в левой и пра-

вой частях равенства, будем иметь

x = −1

24 = 8A, A = 3

x = 0

23 =13A + C, C = 23 -13 ×3 = -16

1 = A + B, B =1 - A =1 - 3 = -2.

Таким образом,

x 2 + 23

2x +16

+1)(x 2 + 6x +13)

x +

x 2 + 6x +13

159

Вычислим далее интегралы от найденных дробей:

2x +16

x + 3 = t,

d (x +1)

2(t - 3) +16

∫

dx - ∫

dx =

x = t - 3,

= 3∫

- ∫

dt =

x +1

(x + 3) 2 - 9 +13

x +1

t 2 + 4

dx = dt

= 3ln

x +1

∫

d (t 2 + 4)

-10∫

= 3ln

x +1

- ln

t 2 + 4

- 5arctg

t 2 + 4

x + 3

= 3ln

x +1

- ln

x 2 + 6x +13

- 5arctg

+ C .

Задания к зачету (нулевой вариант)

¶f ,

¶f , если

f ( x, y ) = e

+ cos 2xy + 9x 7 y 2 .

Вычислить

¶x

¶y

Вычислить:

а)

∫cos 2 7xdx ; ∫sin 2 7xdx ; ∫cos3 5xdx ; ∫sin 5 4xdx ;

б) ∫

;

∫

;

∫

;

∫

; ∫

;

+ 9x 2

- 9x 2

7 + 9x 2

7 - 9x 2

9x 2 - 7

∫

xdx

;

9x 2 - 7

в)

∫ xe −3xdx ; ∫ x × ln 5xdx ; ∫ x × cos3xdx ; ∫ x ×sin7xdx ;

∫

3 -

; ∫tg (3 - 2x)dx ;

г)

; ∫sin

dx ;

∫

+ 9x

+ 9x)2011

×5

3x3

×5

x +15 - 2

∫ x

dx ; ∫arcsin xdx ;

∫ x

∫

д)

dx ;

dx .

4 x +15

160

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1516 / 2516 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в папке Высшая математика (РТФ)

#
18.05.20152.77 Mб51умк_Вакульчик_Неопределенный интеграл.pdf
#
18.05.20153.63 Mб42умк_Вакульчик_Опред интеграл.pdf
#
18.05.20154.76 Mб40умк_Вакульчик_Элементы векторной алгебры.pdf
#
18.05.20155.38 Mб46умк_Вакульчик_Элементы линейной алгебры.pdf
#
18.05.20151.33 Mб47умк_Мальцев_Осн дискретной матем.pdf
#
18.05.20153.75 Mб53умк_Пальчик_Теория вероятностей.pdf
#
18.05.20155.68 Mб35умк_Цывис_Диф.уравнения_Ряды.pdf