умк_Вакульчик_Опред интеграл

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Tn = ∑ ti ≈ ∑

2g(H − xi )

где по условию задачи точки xi

заключены на отрезке [0;H].

.pdf

Скачиваний:

Добавлен:

18.05.2015

Размер:

3.63 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 1415 / 2515 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

b∫γ ( x) x

M y

1 + ( f / ( x))2

(VI.9)

b∫γ ( x) f ( x)

M x

1 + ( f / (x))2

(VI.10)

где т –

массу дуги находим по формуле

m = b∫γ ( x)

dx .

1 + ( f / ( x))2

(VI.11)

2.5.

Для

плоской

фигуры,

ограниченной

кривыми

y = f1(x),

y = f 2 ( x ),

f1(x) ≤ f 2 (x) и прямыми x = a, x = b, (a ≤ x ≤ b) стати-

ческие моменты выражаются формулами:

M x

b∫γ ( x)( f 22 ( x) − f12 ( x)) dx ,

(VI.12)

M y = ∫ x γ ( x)( f 2 ( x) − f1 ( x)) dx .

(VI.13)

Координаты центра масс плоской фигуры вычисляются по формулам:

xc = M y m

	1	b
	1	∫ x γ ( x)( f 2	( x) − f1 ( x))dx
=	2	∫ x γ ( x)( f 2	( x) − f1 ( x))dx
	2	a		,	(VI.14)
		a

		b∫γ ( x)( f 2 (x) − f1(x)) dx

						1	∫γ ( x)( f 22 ( x) − f12 ( x))dx
y	c	=	M x	=	2			.	(VI.15)
							b
			m
							∫γ ( x)( f 2 (x) − f1(x)) dx

Обучающая задача 1. Материальная точка М движется прямоли- нейно со скоростью v(t) = 3t2 + 2t + 2 (м/с). Найти путь, пройденный точ- кой за промежуток времени [0;3] . Чему равна средняя скорость движения

за этот промежуток?

Решение. Согласно формуле (VI.1) имеем

S = ∫(3t 2 + 2t + 2)dt = (t 3 + t 2 + 2t ) 30 = 27 + 9 + 6 = 42 (м),

0
vср	=	S	=	42	= 14(м/с) .
vср	=		=		= 14(м/с) .
		t 3

141

Обучающая задача 2. Котел имеет форму параболоида вращения. Радиус его основания R = 3м, глубина H = 5м. Котел наполнен жидкостью, плотность которой γ = 0,8 (г/см3). Вычислить работу, которую нужно за- тратить, чтобы выкачать жид-

кость из котла.

	Решение. Сечение котла
	плоскостью Oxy есть парабола
	(рис. VI.2), уравнение которой
	y = ax 2 . Точка N(3;5) принад-
	лежит параболе, поэтому ее ко-
	ординаты удовлетворяют урав-
	нению параболы, т. е. 5 = а×32,
Рис. VI.2	отсюда a =	5	.

	9

Тогда y = 5 x 2 – уравнение параболы. 9

Работа, затрачиваемая на поднятие тела весом Р на высоту h, равна Рh. Но различные слои жидкости в котле находятся на различных глубинах и высота поднятия до края котла различных слоев неодинакова. Для решения задачи применяем так называемый «метод дифференциалов» (общая схема II).

1.Работа, затрачиваемая на выкачивание слоя жидкости, толщи- ной y, y Î[0; H ], есть функция от y, т. е. A = A(y).

2.Находим главную часть приращения A при изменении y на ве-

личину dy, т. е. находим дифференциал dA функции A(y).

Ввиду малости dy считаем, что «элементарный слой» жидкости на-

ходится на одной глубине (5 –

y) от края котла (см. рис. VI.2).

Тогда

dA = dР(5 − y), dР = γgdV ,

где dР –

вес этого слоя; g –

ускорение свободного падения; g – плотность

жидкости,

dV –

объем «элементарного слоя» жидкости.

Очевидно,

dV = px 2dy ,

т. к. элементарный слой представляет собой

цилиндр с высотой dy , радиусом основания х.

Так как из уравнения параболы x 2 =

y ,

то dV = p

ydy .

Тогда dР = gg

ydy, а

dA = gg

y(5 - y)dy.

142

Учитывая, что 0 ≤ y ≤ 5 , получим

5	9p		y (5 - y )dy =				9p			5	(5 y - y 2 )dy =				9p					5 y		2		y	3	5
5										5												2			3	5
A = ∫gg								gg		∫							gg						-			=
A = ∫gg								gg		∫					5		gg			2			-			=
0	5					5				0					5					2			3
0										0																0
		9p		125		125				9 ×125			1			1			75							0
		9p		125		125				9 ×125			1			1			75
	=			gg	-				=			pgg		-				=			πγg .
	=	5		gg	-	3			=		5	pgg	2	-				=	2		πγg .
		5		2		3					5		2			3			2

Подставив вместо g = 800 кг/м3, g = 9,8 м/с2, получим

A = 75 p ×800 ×9,8 = 30000 ×9,8p » 294300(Дж). 2

Обучающая задача 3. Найти давление воды (плотность g ) на верти- кальный прямоугольный шлюз с основанием 18 м и высотой 6 м.

Решение. Введем систему координат, как указано на рис. VI.3.

О		y
x	М	N
x		dx
		dx

Рис. VI.3

Давление жидкости на различные слои шлюза разное: зависит от глу- бины погружения x. Для решения задачи применим «метод дифференциа-

ла» (общая схема II).		P есть функция от x: P = P ( x) –
1.	Пусть часть искомой величины	P есть функция от x: P = P ( x) –
давление	на часть прямоугольника,	соответствующая	отрезку [0; x] ,
x Î[0;6] .
2.	Дадим аргументу приращение dx. Функция P ( x)		получит прира-

щение dP (на рис. VI.3 это полоска – слой толщиной dx). Найдем диффе- ренциал dP этой функции. Ввиду малости dx будем приближенно считать полоску прямоугольником, все точки которого находятся на одной глубине x.

Тогда по закону Паскаля dP = gg MN × dx × x = gg ×18xdx .

3.Интегрируя полученное равенство в пределах от x = 0 до x = 6,

получим

6	6	x	2	6	6

P = ∫gg18xdx =18gg ∫ xdx =18gg				= 9gg x 2		= 324gg(кН) .
		2
0	0			0	0

143

Обучающая задача 4. При условиях предыдущей задачи найти, на какой глубине x = c надо разделить шлюз горизонтальной прямой, чтобы давление воды на верхние и нижние части шлюза было одинаково.

Решение. Определим давление воды на каждую часть шлюза, интег- рируя dр в пределах от 0 до c и в пределах от c до 6, затем приравниваем интегралы друг другу:

; получим уравнение x 2

c = x 2

6 .

18gg ∫ xdx =18gg ∫ xdx =

» 4, 23(м).

Отсюда c 2 = 36 - c 2 , 2c 2 = 36, c 2 =18, c = 3

Обучающая задача 5. Найти коорди-

наты центра масс однородной дуги полуок-

ружности и момент инерции относительно

оси Ох (рис. VI.4).

– R

Решение.

Применим формулу

(VI.10),

учитывая, что γ(x) = 1. Согласно формуле

Рис. VI.4

(VI.5), имеем

R 2 - x 2

= 2R 2 .

M x = ∫

1 +

dx = R ∫

dx = R x

−R

R 2 - x

− R

−R

l = πR ,

Так как l –

длина дуги полуокружности с радиусом R, то

а т. к. γ = 1, то т = l.

Тогда yc =

M x

2R 2

, xc = 0, т. к. центр масс находится на оси

симметрии, а осью симметрии является ось Oy. Находим момент инерции дуги относительно оси Ox по формуле (VI.7)

I x = ∫ (R 2 - x 2 )

1 +

dx = R ∫

R 2 - x 2 dx =2R ∫ R 2 - x 2 dx =

2 - x 2

−R

x = R sin t,

dx = R cos t dt,

- R 2 sin 2 t

= 2R 2

= 0, x

= R

= 2R ∫

R 2

× R cost dt

∫ cos 2 t dt =

= p

= 0, t 2

2 p +

= pR 2 .

= R 2 ∫2 (1 + cos 2t ) dt = R

2 t +

sin 2t

2 = R

sin p

144

	Обучающая задача 6. Найти центр тяжести фигуры, расположенной
в первой четверти и ограниченной эллип-																															y	3
сом	4x 2 + 9 y 2 = 36												и	окружностью																		3				x	2	+ y	2
сом	4x 2 + 9 y 2 = 36												и	окружностью																		2				x		+ y	= 9
x 2 + y 2 = 9			(рис.						VI.5).					Положить, что												4x2 + 9y2 = 36						2
x 2 + y 2 = 9			(рис.						VI.5).					Положить, что												4x2 + 9y2 = 36
γ(x) = 1.																																								x
	Решение. Вычислим сначала статиче-																													0								3
ские	моменты						по				формулам							(VI.12),
ские	моменты						по				формулам							(VI.12),													Рис. VI.5
(VI.13), учитывая, что γ(x) = 1.																															Рис. VI.5
(VI.13), учитывая, что γ(x) = 1.
	M x		=		1 ∫ (			f 22 (x) - f12 (x)) dx =											1 ∫		(9 - x 2 ) - 4 (9 - x 2 ) dx =
						3														3
				2 0															2 0									9
				1		3				5					1				5					3			5				x 3		3
												2										3
												2										3
			=			∫	5	-			x		dx =			5x -					x					=		x -					= 5 ,
			=	2		∫	5	-		9	x		dx =		2	5x -			27		x					=	2	x -					= 5 ,
				2						9					2				27								2			27
						0															- 2			0									0
						0																		0
M y	= ∫ x ( f 2 (x) - f1(x))dx = ∫ x																9 - x 2
M y	= ∫ x ( f 2 (x) - f1(x))dx = ∫ x																9 - x 2								9 - x 2 dx = 1 ∫ x 9 - x 2 dx =
	3													3																				3
	0													0								3								3 0
								1									1 × 2(9				- x		2	)		3	3								3		3
																										3	3

= - 1 ∫(9 - x 2 )																										2		= - 1
= - 1 ∫(9 - x 2 )								− 2 d (9 - x 2 ) = -																				= - 1			×(9 - x 2 )2						= 3.
		3

	6	0															6				3							9									0
		0
																											0


Так как γ(x) = 1, то масса фигуры численно совпадает с ее площадью.
	Площадь четверти круга радиуса 3 равна																										9p		, а площадь четверти эл-
	Площадь четверти круга радиуса 3 равна																												, а площадь четверти эл-

липса с полуосями а = 3 и b = 2 равна 1 pab = 3p , поэтому площадь рас- 4 2

сматриваемой фигуры S = 9p - 3p = 3p. Таким образом,

M y

;

M x

Обучающая задача 7. Водопроводная труба имеет диаметр 6 см, один ее конец соединен с баком, в котором уровень воды на 100 см выше верхнего края трубы, а другой закрыт заслонкой. Найти полное давление на заслонку.

145

Решение. Заслонка представляет собой круг радиусом 3 см. Разобьем площадь этого круга на элементы – полоски, параллельные поверхности воды. Площадь одного такого элемента, находящегося на расстоянии y от центра, равна (с точностью до бесконечно малых высшего порядка)

dS = 29 - y 2 dy . Найдем силу давления, испытываемую этим элементом:

dP = 2gg (103 - y ) 9 - y 2 dy =1960(103 - y ) × 9 - y 2 dy

(здесь γ = 1 г/см3). Следовательно,

	3		(103 - y )										y				9		y
	3					9 - y 2 dy =1960 103										9 - y 2 +
P =1960 ∫																		arcsin		+
P =1960 ∫																		arcsin		+
	−3													2		2			3
y				9			y		1				3		3


		9 - y 2 +								(9		2 )2
+103					arcsin			+			- y					= 980 ×927p » 0,09p .
+103				2	arcsin			+	3		- y					= 980 ×927p » 0,09p .
2				2	3				3
															−3
															−3

Ответ: » 0,09p(Дж).

Обучающая задача 8 (повышенный уровень). Найти давление во-

ды на поверхность шара диаметром 4 м, если его центр находится на глу- бине 3 м от поверхности воды.

Решение. Проведем через центр шара вертикальную плоскость и выбе- рем на ней прямоугольную систему координат Oxy, как показано на рис. VI.6.

3м

Рис. VI.6

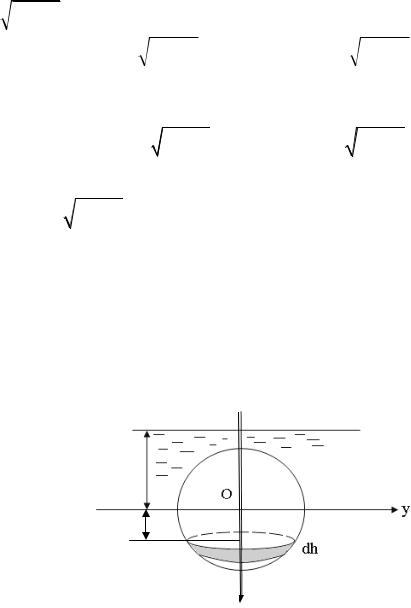
Рассечем шар на глубине h горизонтальной плоскостью. Тогда дав- ление воды на отсеченную часть поверхности шара будет некоторой функ- цией P(h).

При изменении h на величину dh площадь S отсеченной поверхности шара как площадь поверхности вращения вокруг оси Oу изменится на ве- личину dS = 2πydl , где dl – дифференциал дуги окружности, а давление p(h) изменится на величину dp = 2πhydl .

146

Выразив dр через одну переменную x и интегрируя в пределах от x = −2 до x = 2 , найдем давление воды на всю поверхность шара. Из урав-

нения окружности x 2 + y 2 = 4 найдем y¢ = - x и затем

dl =

dx = 1 +

x 2

dx =

x 2 + y 2

dx =

dx;

1 + ( y¢) 2

y 2

Из рисунка находим h = 3 + x . Следовательно,

р = 2p ∫2 (3 + x) y ×

dx = 4p ∫2 (3 + x)dx = 2p(3 + x) 2

» 470880p(H) .

−2

Давление на верхнюю половину поверхности шара получим, интег- рируя dр в пределах от – 2 до 0:

р = 2p(3 + x ) 2	0	»156960p(H) .

1	−2

Давление на нижнюю половину поверхности будет

р2 = 2p(3 + x)2 2 » 313920p(H) .

Обучающая задача 9 (повышенный уровень). Шар лежит на дне бассейна глубиной H = 14 дм. Найти работу, необходимую для извлечения шара из воды, если его радиус R = 3 дм, а удельный вес δ = 2.

Решение. При подъеме шара до поверхности воды сила P1 , совер- шающая работу, постоянна и равна разности между весом шара и весом вытесняемой им воды:

P =	4	pR 3d -	4	pR 3	=	4	pR 3 (d -1) .

1	3	3			3

Поэтому работа A1 , необходимая для поднятия шара до поверхности воды, определяется элементарным путем, как произведение силыP1 на вы-

соту подъема( H - 2R) :

A = P		(H - 2R) =	4	pR 3 (d -1)( H - 2R) .

1	1	3

При дальнейшем подъеме шара сила Р, со-
вершающая работу, будет изменяться в зависимо-
сти от высоты х надводной части шара (рис VI.7):
		P(x) = Pш − Pв ,
где Pш –	вес шара; Pв – вес воды, вытесняемой
подводной частью шара, численно равный объему
шарового сегмента с высотой h = 2R – x .					Рис. VI.7

147

Так как объем шарового сегмента вычисляется по формуле:

V= pH 2 R - 1 H ,

то в нашем случае

	2		1			p	(2R - x)	2	( R + x) =	p	(x	3		2		3	).
Pв = pH		R -		H	=								- 3Rx		+ 4R
Pв = pH		R -	3	H	=	3				3			- 3Rx		+ 4R
			3			3				3

Очевидно и работа, совершаемая силой Р(х), будет некоторой функ- цией А(х). Допуская, что при подъеме шара еще на малую высоту dx сила Р(х) остается неизменной, найдем приближенную величину приращения работы:

dA = P ( x)dx = ( Pш - Pв )dx = p3 (4R 3 (d -1) - x 3 + 3Rx 2 )dx .

Интегрируя dA в пределах от x = 0 до x = 2R, найдем работу A2 , ко-

торую надо совершить, чтобы шар, поднятый со дна бассейна до поверх- ности, полностью извлечь из воды:

(4R 3 (d -1) - x 3 + 3Rx 2 )dx =

3 (d -1)x -

+ Rx 3

2R =

∫

=4 pR 4 (2d -1) .

Вся искомая работа:

A = A1 + A2 = 4 pR 3 (R + (d -1)H ) =

=4 p × 27(0,3 + (2 -1) ×1, 4) ≈ 600,4π (Дж). 3

Обучающая задача 10 (повышенный уровень). Прямоугольный резервуар с площадью горизонтального сечения S = 6м2 наполнен водой до высоты Н = 5 м. Определить время, в течение которого вся вода вытечет из резервуара через небольшое отверстие в его дне площадью S1 = 0,01 м2,

если принять, что скорость истечения воды равна 0,62gh , где h – высота уровня воды над отверстием; g – ускорение силы тяжести.

Решение. Согласно общей схеме I, разобьем искомое время Т на большое число маленьких промежутков t1 , t2 , …, t n и пусть за каж-

148

дый такой промежуток уровень воды в резервуаре понижается на величину

x = H (рис. VI.8). n

Если допустить, что в течение каждого малого промежутка времени ti скорость истечения воды через от-

верстие в дне остается постоянной, рав- ной ее значению в начале промежутка

0,62g(H − xi ) , то прибавление в объ-

еме воды, вытекающей с такой скоро- стью через отверстие в дне за промежу- ток ti , равно объему опорожнившейся

за этот же промежуток части резервуа-								Рис. VI.8
ра, получим приближенно равенство								Рис. VI.8
ра, получим приближенно равенство
							ti ≈ S x .
			0,6S1		2g(H − xi )		ti ≈ S x .
Откуда	ti	≈		S x		.



			0,6S1 2g(H − xi )

Приближенное значение всего искомого времени Тп будет равно сумме

Убедившись, что с возрастанием n погрешность полученного при- ближенного значения Т стремится к нулю, найдем точное значение Т как предел интегральной суммы (*) при n → +∞ , т. е. как соответствующий определенный интеграл:

−

0 =

T =

( H − x)

2 dx =

( H − x)

∫

0,6S1

0,6S1 2g

Подставляя числовые значения параметров S = 6, H = 5,

S1 = 0,01,

g = 9,81, получим T ≈ 1019 с ≈ 16,99 мин.

Если бы убыль воды в резервуаре постоянно возмещалась, т. е. если бы уровень воды в нем оставался неизменным, то и скорость истечения во-

ды была бы постоянной, равной 0,62gh . В этом случае в каждую секун-

ду через отверстие в дне резервуара будет вытекать объем воды 0,62gH .

149

Поэтому при указанном предположении объем воды, вмещающийся в ре-

Сопоставление этого результата с предыдущим показывает, что время истечения Т без возмещения убыли воды в резервуаре, в два раза больше времени истечения T1 при постоянном возмещении убыли воды; T = 2T1 .

Обучающая задача 11. Цилиндр высотой H = 1,5 м и радиусом R = 0,4 м наполнен газом под атмосферным давлением (10330 кг/м2) и за- крыт поршнем. Определить работу, затрачиваемую на изотермическое сжа- тие газа при перемещении поршня на расстояние h = 1,2 м внутрь цилиндра.

Решение. При изотермическом изменении состояния газа, когда его температура остается неизменной, за- висимость между объемом V и давле- нием р газа выражается формулой pV = c = const (Закон Бойля – Мари- отта) рис. VI.9.

Поэтому, если поршень будет вдвинут на х м внутрь цилиндра (см.

рис. VI.9), то давление р(x) газа на единицу площади поршня будет


	c		c
p(x) =		=			,
	V ( x)		S ( H − x)
а давление на всю площадь S поршня будет
P(x) = Sp(x) =			c
				.

H − x

Полагая, что работа, затрачиваемая при продвижении поршня на х м есть некоторая функция А(х), и допуская, что при дальнейшем продвиже- нии поршня на малое расстояние dx испытываемое им давление p(х) оста- ется неизменным, найдем дифференциал функции А(х):

dA ≈ р(x)dx =	c
		dx .

	H − x

Всей искомой работе А соответствует изменение х от 0 до h, поэтому

h = c ln

A = c∫

= −c ln

H − x

H − h

При H = 1,5 м, R = 0,4 м, h = 1,2 м, p0 =10330 кг/м2 найдем

V0 = πR 2 H = 0, 24π м3; с = p0 ×V0 = 2479, 2p . А ≈ 122951,7 (Дж).

150

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 1415 / 2515 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в папке Высшая математика (РТФ)

#
18.05.20152.77 Mб51умк_Вакульчик_Неопределенный интеграл.pdf
#
18.05.20153.63 Mб42умк_Вакульчик_Опред интеграл.pdf
#
18.05.20154.76 Mб40умк_Вакульчик_Элементы векторной алгебры.pdf
#
18.05.20155.38 Mб46умк_Вакульчик_Элементы линейной алгебры.pdf
#
18.05.20151.33 Mб47умк_Мальцев_Осн дискретной матем.pdf
#
18.05.20153.75 Mб53умк_Пальчик_Теория вероятностей.pdf
#
18.05.20155.68 Mб35умк_Цывис_Диф.уравнения_Ряды.pdf