Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

умк_Вакульчик_Опред интеграл

.pdf

Скачиваний:

Добавлен:

18.05.2015

Размер:

3.63 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 2324 / 2524 25 > Следующая >>>

7. Найти вторые частные производные указанной функции. Убедиться в

том, что	′′	′′
том, что	zxy	= z yx .

z= arcsin ( x − y ) .

8.Исследовать на экстремум следующую функцию:

z = 3x3 + 3y3 − 9xy + 10 .

Ответ: zmin (1, 1) = 7. 9. Найти наибольшее и наименьшее значения функции z = z ( x, y ) в об-

ласти D, ограниченной заданными линиями.

	z = 2x3 − xy2 + y2 , D: х = 0, х = 1, у = 0, у = 6.
	Ответ:	zнаиб. (0, 6) = 36, zнаим. (0, 0) = 0.
	Вариант 7
1.	Найти область определения функции z = arccos( x + y ) .

2.	Найти частные производные функции	z = ctg xy3 .
3.	Найти полный дифференциал функции	z = ln (3x2 − 2 y2 ) .
4.	Вычислить значение производной сложной функции u = u(x, y), где x = x(t),
	y = y(t) при t = t0 с точностью до двух знаков после запятой.
	u = x y , x = et , y = ln t , t		0	= 1.
			0

Ответ: 1.

5.Вычислить значения частных производных функции z(x, y), заданной неявно, в точке М0(х0, у0) с точностью до двух знаков после запятой.

z3 + 3xyz + 3 y = 7 ,	М0(1, 1, 1).
Ответ:	′	(1, 1, 1) = −0,5,	′	(1, 1, 1) = − 1.
	zx		z y

6.Найти уравнения касательной плоскости и нормали к заданной поверх- ности S в точке М0(х0, у0, z0).

S: x2 + y 2 + z2 − 6 y + 4z + 4 = 0 , М0(2, 1, −1).

Ответ: 2x − 2 y + z −1 = 0 .

7. Найти вторые частные производные указанной функции. Убедиться в

том, что	′′	′′
том, что	zxy	= z yx .

z= arctg ( x + y ) .

8.Исследовать на экстремум следующую функцию:

z = 2x3 + 2 y3 − 6xy + 5 .

Ответ: zmin (1, 1) = 3.

231

9.Найти наибольшее и наименьшее значения функции z = z ( x, y ) в об-

ласти D, ограниченной заданными линиями.

z = x2 + y 2 − 2x − 2 y + 8 , D: х = 0, у = 0, х + у – 1 = 0.

	Ответ: zнаиб. (0, 0) = 8,			zнаим. (0,5; 0,5) = 6,5.
	Вариант 8
1.	Найти область определения функции z = 3x +		y		.

			− x
		2		+ y
2.	Найти частные производные функции	z = e− x2 + y2 .
3.	Найти полный дифференциал функции	z = 5xy2 − 3x3 y4 .
4.	Вычислить значение производной сложной функции u = u(x, y), где x = x(t),
	y = y(t) при t = t0 с точностью до двух знаков после запятой.
	u = e y −2 x , x = sin t , y = t3 ,	t0 = 0 .

Ответ: − 2.

x2 + y 2 + z2 − z − 4 = 0 , М0(1, 1, − 1).

Ответ:	′	(1, 1,	−1) = 0,67,	′	(1, 1,	− 1) = 0,67.
	zx			z y

6.Найти уравнения касательной плоскости и нормали к заданной поверх- ности S в точке М0(х0, у0, z0).

S: 2x2 − y2 + z 2 − 4z + y = 13 , М0(2, 1, −1).

Ответ: 8x − y − 6z − 21 = 0 .

7. Найти вторые частные производные указанной функции. Убедиться в

том, что	′′	′′
том, что	zxy	= z yx .

z= sin (x2 − y).

8.Исследовать на экстремум следующую функцию:

z = x3 + y2 − 6xy − 39x + 18 y + 20 .

Ответ: zmin (5, 6) = − 86. 9. Найти наибольшее и наименьшее значения функции z = z ( x, y ) в об-

ласти D, ограниченной заданными линиями.

z = x2 + 2xy − y2 − 4x , D: х – у + 1= 0, х = 3, у = 0.

Ответ: zнаиб. (3, 3) = 6, zнаим. (2, 0) = − 4.

232

	Вариант 9

1.	Найти область определения функции z =	9 − x2 − y2 .
2.	Найти частные производные функции	z = ln (3x2 − y4 ).
3.	Найти полный дифференциал функции	z = arcsin ( x + y ) .
4.	Вычислить значение производной сложной функции u = u(x, y), где x = x(t),
	y = y(t) при t = t0 с точностью до двух знаков после запятой.

u = x2e− y , x = sin t , y = sin 2 t , t0	= π .
	2
	Ответ: 0.

ez + x + 2 y + z = 4 ,	М0(1, 1, 0).
Ответ:	′	(1, 1, 0) = − 0,5,	′	(1, 1, 0) = − 1.
	zx		z y

6.Найти уравнения касательной плоскости и нормали к заданной поверх- ности S в точке М0(х0, у0, z0).

S: x2 + y2 + z 2 + 6 y + 4x = 8 , М0(− 1, 1, 2).

Ответ: x + 4 y + 2z − 7 = 0 .

7. Найти вторые частные производные указанной функции. Убедиться в

том, что	′′	′′
том, что	zxy	= z yx .

z= cos(xy2 ).

8.Исследовать на экстремум следующую функцию:

z = 1 + 6x − x2 − xy − y2 .

Ответ: zmax (4, -2) = 13.

9.Найти наибольшее и наименьшее значения функции z = z ( x, y ) в об-

ласти D, ограниченной заданными линиями.

z = 5x2 − 3xy + y 2 , D: х = 0, х = 1, у = 0, у = 1.

Ответ: zнаиб. (1, 0) = 5, zнаим. (0, 0) = 0.

Вариант 10

1. Найти область определения функции z = ln (x2 + y2 − 3).

		y
2. Найти частные производные функции	z = arccos		.

		x

233

3.	Найти полный дифференциал функции	z = arctg (2x − y ) .
4.	Вычислить значение производной сложной функции u = u(x, y), где x = x(t),
	y = y(t) при t = t0 с точностью до двух знаков после запятой.
	u = ln (e− x + e y ) , x = t 2 , y = t3 , t0 = −1.

Ответ: 2,5.

3x − 2 y + z = xz + 5 ,	М0(2, 1, − 1).
Ответ:	′	(2, 1, – 1) = 4,	′	(2, 1,	− 1) = − 2.
	zx		z y

6.Найти уравнения касательной плоскости и нормали к заданной поверх- ности S в точке М0(х0, у0, z0).

S: x2 + y2 + z2 − xy + 3z = 7 , М0(1, 2, 1).

Ответ: 3y + 5z −11 = 0 .

7. Найти вторые частные производные указанной функции. Убедиться в

том, что	′′	′′
том, что	zxy	= z yx .

z = tg x . y

8. Исследовать на экстремум следующую функцию z = 1 + 15x − 2x2 − xy − 2 y2 .

Ответ: zmax (−4, −1) = −97. 9. Найти наибольшее и наименьшее значения функции z = z ( x, y ) в об-

ласти D, ограниченной заданными линиями.

z = x2 + 2xy − 4x + 8 y , D : х = 0, х = 1, у = 0, у = 2.

Ответ: zнаиб. (1, 2) = 17, zнаим. (1, 0) = −3.

УРОВЕНЬ II

Вариант 1

1.Проверить, удовлетворяет ли указанному уравнению данная функ-

ция и.

2 ∂2u + 2xy

∂2u

+ y

2 ∂2u

= 0 ,

u =

∂x∂y

∂y2

∂x2

Вычислить приближенно sin 2 1,55 + 8e0,015

= 1,571, y0

= 0

Ответ: 3,02.

234

3.Найти производную функции z = x2 − y2 в точке М(1, 1) в направ-

лении вектора S , составляющем угол α = 60° с положительным на- правлением оси Ох.

Ответ: −0,7.

4.Найти экстремум функции z = x2 + y2 , если х и у связаны уравне-

нием x + y = 1. 4 3

	=	144		36	48
Ответ: zmin			в		,	.
		25
			25		25

Вариант 2

1.Проверить, удовлетворяет ли указанному уравнению данная функ-

ция и.

x ∂u + y

∂u = 3(x3 − y3 ),

u = ln

+ x3 − y3 .

∂x

∂y

Вычислить приближенно

arctg

1,02

0,95

Ответ: 0,82

Найти производную функции u = arcsin

в точке М(1, 1, 1)

x2 + y2

в направлении вектора MN , где N(3, 2, 3).

Ответ: 1 . 6

4.Найти наименьшее и наибольшее значения функции z = 1 − x2 − y2 в круге ( x −1)2 + ( y −1)2 ≤ 1.

Ответ: zнаим. = −2(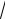2 + 1) , zнаиб. = 2(2 −1) .

Вариант 3

1.Проверить, удовлетворяет ли указанному уравнению данная функ-

	ция и.	∂2u +	∂2u = 0 , u = ln (x2	+ ( y + 1)2 ).
		∂x2	∂y2
2.	Вычислить приближенно		1,024,05 .
	Найти производную функции u = ln (x2 + y 2 + z 2 )			Ответ: 1,08.
3.	Найти производную функции u = ln (x2 + y 2 + z 2 )			в точке М(1, 2, 1)

в направлении вектора r = 2i + 4 j + 4k .

Ответ: 7/9.

235

4.Из всех прямоугольников с заданной площадью S найти такой, пе- риметр которого имеет наименьшее значение.

Ответ: квадрат, Pнаим. = 4S .

Вариант 4

1.Проверить, удовлетворяет ли указанному уравнению данная функ-

ция и.

∂2u

= (1 + y ln x)

∂u , u = x y .

∂x∂y

∂x

Вычислить приближенно

1,022 + 0,052

Ответ: 1,013.

Найти

величину

и направление

градиента функцииu =

где

( x , y

) .

r = x

2 + y 2 + z2

в точке M

, z

Ответ:

grad u

, cos α = −

, cosβ = −

, cos λ = −

M 0

где r =

+ y

2 + z

2 .

4.Найти размеры прямоугольного параллелепипеда, имеющего при данной полной поверхности S максимальный объем.

Ответ: куб с ребром S . 6

Вариант 5

1.Проверить, удовлетворяет ли указанному уравнению данная функ-

ция и.

x ∂u + y

∂u = 2u , u =

∂x

∂y

x + y

Вычислить приближенно

1,041,99 + ln1,02

Ответ: 1,05.

Найти производную функции u =

в направлении вектора

= 6i + 3 j − 6k

в произвольной точке.

Ответ: 1/3.

4.Определить размеры прямоугольного параллелепипеда данного объ- ема V, имеющего поверхность наименьшей площади.

Ответ: куб с ребром 3V .

236

Вариант 6

1.Проверить, удовлетворяет ли указанному уравнению данная функ-

	ция и.	x	2 ∂2u + y	2 ∂2u = 0 ,		u = exy .
			∂x2	∂y 2
				ln (3		+ 4		−1).
2.	Вычислить приближенно				1,03		0,98

Ответ: 0,005.

3.Найти производную функции u = xy 2 + z3 − xyz в точке М(1, 1, 2) в

направлении, образующем с осями координат углы соответственно в

60°, 45°, 60°.

						Ответ: 5.
4.	Исследовать на экстремум функцию				z = xy при	условии
	x2 + y 2 = 2a2 .
	Ответ: z		max	= a2	в точках (а, а) и (−а, −а);
			max
	z	min		= −a2	в точках (а, −а)	и (−а, а).
		min

Вариант 7

1.Проверить, удовлетворяет ли указанному уравнению данная функ-

	ция и.	a2 ∂2u =		∂2u	,	u = sin 2 ( x − ay ) .
			∂x2	∂y2
2.	Вычислить приближенно		1,042,02 .

Ответ: 1,08.

3.Найти производную функции u = xyz в точке А(5, 1, 2) в направле-

нии, идущем от этой точки к точке В(9, 4, 14).

Ответ: 98 .

Исследовать на экстремум функцию

z =

при

условии

x y

Ответ: z

max

в точке ( a

2 , a

2 );

= −

в точке (− a

, − a

min

2 ).

237

Вариант 8

1.Проверить, удовлетворяет ли указанному уравнению данная функ-

	ция и.	x2 ∂2u − y	2 ∂2u	= 0 ,	u = y	y	.
	ция и.	x2 ∂2u − y	∂y2	= 0 ,	u = y		.
		∂x2	∂y2			x
2.	Вычислить приближенно изменение функции z =							x + 3y	при измене-
2.	Вычислить приближенно изменение функции z =								при измене-
								y − 3x
	нии х от х1 = 2	до х2 = 2,5	и у	от у1 = 4 до у2 = 3,5.
									Ответ:7,5.

3.Найти производную функции u = x2 y2 z2 в точке А(1, -1, 3) в направ-

лении, идущем от этой точки к точке В(0, 1, 1).

Ответ: −22.

4.Разложить положительное число а на три положительных слагае- мых так, чтобы произведение их было наибольшим.

Ответ: x = y = z.

Вариант 9

1.Проверить, удовлетворяет ли указанному уравнению данная функ-

	ция и.	∂2u +	∂2u +	∂2u = 0 , u =			1	.
	ция и.	∂2u +	∂2u +	∂2u = 0 , u =				.
		∂x2	∂y2	∂z 2			x2 + y2 + z 2

2.	Вычислить приближенно				4,052 + 3,072	.
							Ответ: 5,082.
3.	Температура	тела	в	пространстве			задается	функцией

T = x2 y + yz − exy . Найти скорость изменения температуры в точке

М(1, 1, 1) в направлении от этой точки к началу координат.

Ответ: 2e − 5 . 3

4.Представить положительное число а в виде произведения четырех положительных множителей так, чтобы их сумма была наименьшей.

Ответ: все четыре множителя равны между собой.

Вариант 10

1.Проверить, удовлетворяет ли указанному уравнению данная функ-

ция и.	a	2 ∂2u		=	∂2u		,	u = e	− cos( x+ay )	.
		∂x	2		∂y	2

238

2.	Вычислить приближенно	arctg	1,02	.

		0,95

Ответ: 0,82.

3.Найти производную функции z = arctg ( xy ) в точке М(1, 1) в направ-

лении биссектрисы первого координатного угла.

									Ответ:	2	.
									Ответ:	2	.
										2
4.	Найти	наименьшее	и	наибольшее	значения				функции
	z = e− x2 − y2 (2x2 + 3y2 ) в круге x2 + y 2 £ 4 .
		Ответ: zнаим. = 0		в точке (0, 0);	zнаиб.	=	3	в точках (0, ±1).
		Ответ: zнаим. = 0		в точке (0, 0);	zнаиб.	=		в точках (0, ±1).
							e

УРОВЕНЬ III

1.Доказать, что функция

x3 y

если x6 + y2 ¹ 0,

f ( x, y) =

x6 + y2

0, если x = y = 0,

разрывна

при х = у = 0,

но имеет частные производные в точке

О(0, 0).

Доказать, что для функции

xy (x2 - y2 )

если x2 + y 2

¹ 0,

+ y2

f ( x, y ) =

если x = y = 0,

выполняется неравенство

f xy′′

(

0,0) ¹ f yx′′

(0,0) .

Найти

наибольшее

наименьшее

значения

функции

z =

x + y

- 1 - x2 - y 2

в области ее непрерывности.

Ответ: zнаим. = −1,

zнаиб. =

2 .

Записать

уравнение

yz¢¢

+ 2z¢

новых

переменных

u =

v = x − y .

u 2 (u -1)

2u (u -1)

2(u -1)

Ответ:

z¢¢

+ 2uz¢¢

z¢¢

z¢

- 2z¢

u -1 vv

239

5. Записать в полярных координатах выражение ∂2 z + ∂2 z .

∂x2 ∂y 2

Ответ:

∂2 z

1 ∂2 z

1 ∂z

∂ρ2

ρ2 ∂ϕ2

ρ ∂ρ

Найти

уравнение касательной плоскости

эллипсоиду

y 2

z 2

= 1, отсекающей на осях координат равные отрезки.

Ответ: ± x ± y ± z =

a2 + b2 + c2 .

7.Доказать, что касательная плоскость к поверхности xyz = a3 в любой ее точке образует с координатными плоскостями тетраэдр постоян- ного объема. Вычислить этот объем.

Ответ: V = 9 a3 . 2

8.Найти стороны треугольника данного периметра 2р, который при вращении вокруг одной из своих сторон образует тело наибольшего объема.

				Ответ: a = b =						3 p			, c =				p			.
				Ответ: a = b =									, c =							.
					4											2

					1											3
					1											3
9.	На эллипсе x2 + 4 y2 = 4 даны две точки A − 3,					и B							1,					.
9.	На эллипсе x2 + 4 y2 = 4 даны две точки A − 3,					и B							1,					.
					2											2
	Найти на этом эллипсе третью точку			С, такую, чтобы треугольник
	АВС имел наибольшую площадь.
								−1 −							−1
							3	−1 −						3	−1
				Ответ: C							;							.
				Ответ: C	2						;		2					.
					2								2
10.	Найти условный экстремум функции			u = x + y + z			при условиях
	xyz = 8,	xy	= 8 .
	xyz = 8,		= 8 .
		z

				Ответ: x = y = 24								,	z =				2		.
									6								2
									6							3
																3

11.Найти второй дифференциал d 2 z в точке (2, 1, 2) для функции, за- данной неявно уравнением 3x2 y2 + 2xyz 2 − 2x3z + 4 y3z − 4 = 0 .

Ответ: −31,5dx2 + 206dxdy − 306dy 2 .

240

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 2324 / 2524 25 > Следующая >>>

Соседние файлы в папке Высшая математика (РТФ)

#
18.05.20152.77 Mб51умк_Вакульчик_Неопределенный интеграл.pdf
#
18.05.20153.63 Mб42умк_Вакульчик_Опред интеграл.pdf
#
18.05.20154.76 Mб40умк_Вакульчик_Элементы векторной алгебры.pdf
#
18.05.20155.38 Mб46умк_Вакульчик_Элементы линейной алгебры.pdf
#
18.05.20151.33 Mб47умк_Мальцев_Осн дискретной матем.pdf
#
18.05.20153.75 Mб53умк_Пальчик_Теория вероятностей.pdf
#
18.05.20155.68 Mб35умк_Цывис_Диф.уравнения_Ряды.pdf