Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

умк_Вакульчик_Опред интеграл

.pdf

Скачиваний:

Добавлен:

18.05.2015

Размер:

3.63 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 2513 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

4. Если фигура ограничена	прямыми y = c , y = d	и кривыми
x = g1 ( y ) , x = g 2 ( y ) ( g1 ( y ) £ g 2 ( y )	для y Î[ c; d ] ) (рис. IV.4), то ее пло-
щадь определяется формулой
S = d∫( g 2 ( y ) - g1 ( y ) )dy .		(IV.5)
c

	Рис. IV.3		Рис. IV.4
			x = x (t ),
5.
5.	Если кривая задана параметрическими уравнениями
			y = y (t ).

y (t ) ³ 0 ,	t Î[ t1,t2 ] , то площадь криволинейной трапеции, ограниченной
прямыми x = a , x = b , осью абсцисс и кривой, находится по формуле
	t
	S = ∫2	y (t ) x¢(t )dt ,	(IV.6)
	t1
где t1 и t 2 определяются из условий x (t1 ) = a ,			x (t 2 ) = b .
6.	Площадь криволинейного сек-
тора, ограниченного кривой, заданной в
полярных координатах уравнением
r = r(j) и двумя полярными радиусами
ϕ = α , ϕ = β ( α < β ) (рис. IV.5), выража-

ется формулой				Рис. IV.5
ется формулой
	1	β	(j) dj .
S =	1	∫r2		(IV.7)
S =		∫r2		(IV.7)
2		α

121

7. Если фигура ограничена двумя полярными радиусами ϕ = α ,

ϕ = β и кривыми r = r1 (j) , r = r2 (j) , где r1 (j) £ r2 (j) для jÎ[ a,b ]

(рис. IV.6), то ее площадь находится по формуле

S = 1 ∫(r22 (j) - r12 (j)) dj . (IV.8) 2 α

Рис. IV.6

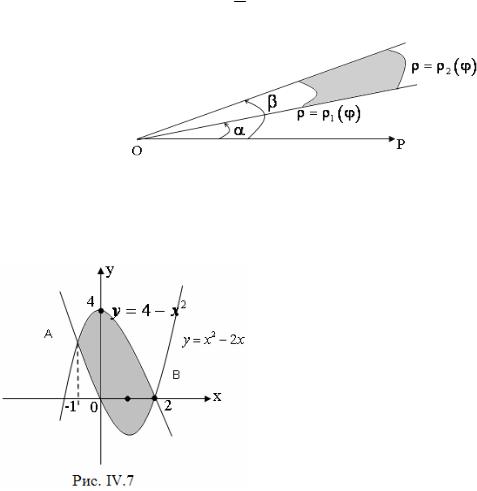
Обучающая задача 1. Вычислить площадь фигуры, ограниченной параболами y = 4 - x 2 и y = x 2 - 2x .

Решение. Найдем точки пересечения данных кривых. Для этого решим систему

уравнений:
	- x	2	,
y = 4	- x		,	- x 2 ,
			x 2 - 2x = 4	- x 2 ,
y = x	2 - 2x.
		2x 2 - 2x - 4 = 0 ,
			x 2 - x - 2 = 0
		x1 = 2 , x2 = −1.

Определив точки пересечения парабол A(-1; 3 ) и B ( 2;0 ) , построив эти точки и параболы (рис. IV.7), видим, что

4 - x 2 ³ x 2 - 2x при x Î[-1;2] . Площадь данной фигуры находим по формуле

S = b∫( f 2 ( x) - f1 ( x)) dx .

		a
	2	((4 - x 2 ) - (x 2 - 2x))dx =
	S = ∫	((4 - x 2 ) - (x 2 - 2x))dx =
	−1
2	(4 + 2x - 2x 2 )dx = = 4x + x 2 -		2	x 3	2	= 9 (ед2.).
					2

∫
∫			3
−1			3		−1
−1					−1

122

Обучающая задача 2. Вычислить площадь фигуры, ограниченной
параболами x = -2 y 2 , x =1 - 3y 2 .
Решение. Решая систему уравнений,
построим эти параболы (рис. IV.8)
x = -2 y 2 ,	Найдем ординаты точек пе-
	Найдем ординаты точек пе-
x =1 - 3y 2.
ресечения кривых y1 = −1,					y2 = 1.
Так	как		1 - 3y 2 ³ -2 y 2				при
y Î[-1;1] , то воспользовавшись формулой								Рис. IV.8
S = d∫( g 2 ( y ) - g1 ( y ) )dy , получим								Рис. IV.8
S = d∫( g 2 ( y ) - g1 ( y ) )dy , получим
c								(- y 2 +1)dy =
1					1		1
S = ∫ ((1 - 3y 2 ) - (			-2 y 2 )) dy = ∫ (- y 2 +1)dy = 2∫
−1						−1	0
		y 3		1	4	(ед2.).
		y 3		1	4
= 2	-		+ y	=
= 2	-	3	+ y	=	3
		3			3
				0
				0
Обучающая задача 3. Найти пло-
щадь фигуры (рис. IV.9), ограниченной эл-
липсом x = a cost,								Рис. IV.9
y = bsin t.

Решение. Оси координат совпадают с осями симметрии данного эл- липса (см. рис. IV.9), поэтому они делят его на четыре одинаковые части. Четвертую часть искомой площади S, расположенную в первом квадранте, найдем как площадь криволинейной трапеции, прилежащей к оси Ох.

y (t ) x¢(t )dt . Если x = 0 , то t = p ; ес-

Находим

по формуле S = ∫2

ли x = a , то t = 0 . Будем иметь

- cos 2t

= ∫bsin t (-a sin t ) dt = ab ∫ sin

2 t dt

= ab ∫

dt =

ab p

pab

t -

sin 2t

- 0

(ед

.).

2 2

123

Тогда искомая площадь

S = 4 × 1 S = 4 × pab = pab . 4 4

Отсюда при a = b получается формула для площади круга

S = pa 2 .

Обучающая задача 4. Вычислить площадь фигуры, ограниченной

лемнискатой Бернулли r = a

2cos 2j

Решение. Искомая фигура изображена на

рис. IV.10.

Применяя формулу

S =

∫r2 (j) dj , и

Рис. IV.10

учитывая, что фигура состоит из четырех оди-

наковых частей, имеем

S = 4 ×

∫ (a

2cos 2j

)2 dj =

2a 2 × 2 ∫ cos 2j dj = 2a 2 sin 2j

4 =

= 2a 2 sin p = 2a 2 (ед2.).

Обучающая задача 5. Найти площадь фигуры, вырезаемой окруж-

ностью r =

sin j

ρ = 1 + cos ϕ (рис. IV.11).

из кардиоиды

Решение. Найдем сначала точки пересече-

ния этих кривых. Для этого решим систему

3 sin j,

r =

j1 =

ϕ2 = π .

откуда

r =

1 + cos j,

Площадь заданной фигуры равна сумме

двух площадей, одна из которых представляет

Рис. IV.11

круговой сегмент, а другая сегмент кардиоиды,

причем сегменты примыкают друг к другу по лу-

чу j = p . Дуга ВАО описывается концом полярного радиуса ρ кардиоиды

при изменении полярного угла ϕ от p до π , а дуга ОСВ – концом поляр- 3

ного радиуса ρ окружности при 0 £ j £ p . 3

124

		π				π
Поэтому S =	1	3	2	ϕ dϕ +	1	π	(1 + cos ϕ)2 dϕ =
	1	∫ 3 sin	2		1	∫
		∫ 3 sin				∫
2		0			2	π
						3

			sin 2j			π						j		sin 2j			π
	3					3		1									π			3		2
	3					3		1												3		2
=		j -					+		j + 2sin j +				+				π	=			(p - 3 ) (ед			.).
=		j -					+		j + 2sin j +			2	+					=		4	(p - 3 ) (ед			.).
	4			2		0		2				2			4					4
						0										3
																3
4. У доски студенты решают задачи:
4.1. Найти				площадь						между	параболой
y = -x 2 - 2x + 3 , касательной в точке M ( 2; -5 ) и
осью ординат.
Решение. Уравнение касательной в точке
M ( 2; -5 )		имеет			вид				y + 5 = -6( x - 2)						или
y = 7 − 6x . Ветви параболы направлены вниз,															по-
этому парабола				лежит				под		касательной,					т. е.						Рис. IV.12
7 - 6x ³ -x 2 - 2x + 3 на отрезке [ 0;2 ]											(рис. IV.12).										Рис. IV.12
7 - 6x ³ -x 2 - 2x + 3 на отрезке [ 0;2 ]											(рис. IV.12).
Следовательно,
2										2								x	3				2		8
2										2									3				2
S = ∫((7 - 6x) - (-x 2 - 2x + 3))dx = ∫ (x 2 - 4x + 4)dx =																				-	2x 2 + 4x		=			.
S = ∫((7 - 6x) - (-x 2 - 2x + 3))dx = ∫ (x 2 - 4x + 4)dx =																		3		-	2x 2 + 4x		=			.
0										0								3						3
0										0													0
																							0
4.2. Вычислить площадь фигуры, ограниченной осью Ох и одной ар-

x = a (t - sin t ),

кой циклоиды

y = a (1 - cost )

(рис. IV.13).

Ответ: 3pa 2 (ед2.).

Рис. IV.13

Указание. Находим площадь фигуры по формуле S = ∫ y (t ) x¢(t )dt .

Если x = 0 , то t = 0 ; если x = 2πa , то t = 2π .

125

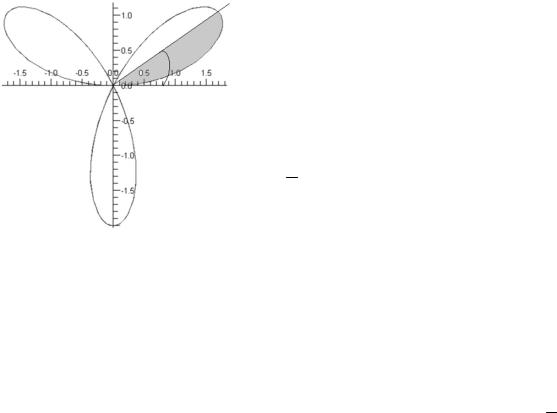
4.3. Найти площадь фигуры, огра- ниченной «трехлепестковой розой»

ρ = a sin 3ϕ .

Ответ: πa 2 . 4

Указание. Используя формулу

S = 1 ∫ρ2 (ϕ) dϕ , найдите шестую часть

2 α

искомой площади (выделена на рис.

IV.14).

Рис. IV.14

Домашнее задание

1.Изучить темы «Вычисление длины дуги кривой», «Вычисление объемов тел и площадей поверхностей вращения».

2.Найти площади фигур, ограниченных данными линиями:

а) y = 2x − x 2 , y = −x .

б) осью Ох и одной аркой циклоиды

x = 2	(t − sin t ),

	(1 − cost ).
y = 2	(1 − cost ).

в) одним лепестком «розы» ρ = a cos 2ϕ , a > 0 .

Повышенный уровень.

г) (x 2 + y 2 )3 = a 2 x 2 y 2 .

Ответ: 4 1 . 2

Ответ: 12.

Ответ: πa 2 . 8

V. Вычисление длин дуг кривых.

Вычисление объемов тел и площадей поверхностей вращения

1. Выяснить вопросы по выполнению домашнего задания и в случае надобности решить вызвавшие затруднения задачи на доске. Рассмотреть формулы вычисления длины дуги кривой.

1.Если дуга кривой задана уравнением y = f ( x) в промежутке [a;b]

ифункция y = f ( x) имеет непрерывную производную в указанном проме-

126

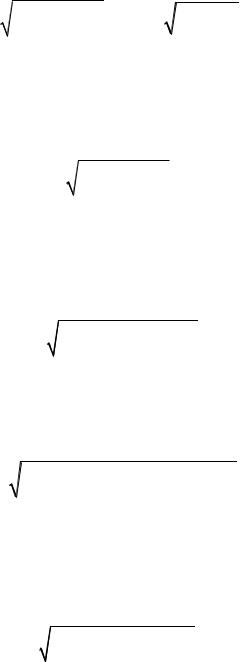
жутке, то длина дуги кривой, содержащейся между двумя точками с абс- циссами x = a , x = b , определяется по формуле

b		b
	1 + ( f ′( x))2

l = ∫		dx = ∫ 1 + ( y′)2 dx	(V.1)
a		a

2. Если кривая задана уравнением x = g ( y ) в промежутке [ c; d ] и

функция x = g ( y ) имеет непрерывную производную в этом промежутке, то длина дуги кривой определяется по формуле

d
l = ∫ 1 + (g′( y ))2 dy .	(V.2)

3. Если кривая задана параметрическими уравнениями				x = x (t ) ,
y = y (t ) , t [t1;t 2 ] , где x (t ) ,		y (t ) – непрерывно дифференцируемые функ-
ции, то длина дуги кривой вычисляется по формуле
	t
	t		( x′(t ))2 + ( y′(t ))2 dt .
l = ∫2			( x′(t ))2 + ( y′(t ))2 dt .	(V.3)
	t1
Если дуга – пространственная кривая x = x (t ) , y = y (t ) ,				z = z (t )
t [t1;t 2 ] , то ее длина определяется формулой
t
t		(t ))2 + ( y′(t ))2 + (z′(t ))2 dt .
l = ∫2 ( x′		(t ))2 + ( y′(t ))2 + (z′(t ))2 dt .		(V.4)
t1

4. Если задано полярное уравнение кривой ρ = ρ(ϕ) , ϕ[α;β] , где

ρ(ϕ) и ρ′(ϕ) непрерывны на отрезке [α;β] , то длина дуги кривой вычисля-

ется по формуле

l = β∫		dϕ .
	(ρ(ϕ))2 + (ρ′(ϕ))2		(V.5)
α

Обучающая задача 1. Вычислить длину дуги полукубической пара- болы y 2 = ( x −1)3 между точками A(2;−1) и B (5; −8) .

Решение. Разрешаем данное уравнение относительно y и находим y′ :

3				3	1
y = ± ( x −1)		;	y′ = ±		( x −1)		.
	2					2

			2

127

Знаки ± в выражении у указывают, что кривая симметрична оси Ох; точки А и В, имеющие отрицательные ординаты, лежат на той ветке кри- вой, которая расположена ниже оси Ох.

Подставляя в формулу I = ∫ 1 + ( y¢)2 dx , получим

		xB						5
		xB			1 + ( y¢)			5
l = ∫					1 + ( y¢)		2 dx = ∫ 1 +
		x A					2
	1		5	1
=			∫	(9x - 5)			d (9x - 5) =
						2
						2
18			2
			2

	9	( x -1) dx =					1	5		dx =
	9						1	∫	9x - 5
4								∫	9x - 5
4					2			2
								2
1		3				5
						5

			(9x - 5)				» 7,63 (ед. длины).
				2
27				2		2
27

Обучающая задача 2. Вычислить длину дуги развертки окружности

x = a (cost + t sin t ),
	от t = 0 до t = 2π .
	от t = 0 до t = 2π .
y = a (sin t - t cos t ).

Решение. Дифференцируя по t, получим

x¢t = (a (cos t + t sin t ))¢ = a (-sin t + sin t + t cos t ) = at cost ,

y¢t = (a (sin t - t cos t ))¢ = a (cost - cost + t sin t ) = at sin t ,

откуда

2π

(x¢(t ))2 + ( y¢(t ))2

a 2t 2 cos 2 t + a 2t 2 sin 2 t dt =

l =

∫

dt = ∫

2π

= ∫ at

cos 2 t + sin 2 t dt = ∫ at dt = a

= 2p2a (ед. длины).

Обучающая задача 3. Вычислить длину дуги кривой r = a cos 3 j .

Решение. Половина этой кривой (рис. V.1) описывается концом по-

лярного радиуса при изменении ϕ от 0 до

p .

Из

данного

уравнения

кривой

r = a cos 3 j

находим производную

r¢(j)

2 j

= 3a cos

-sin

= -a cos

sin

и дифференциал ее дуги

128

dl =

dj =

a 2 cos 6 j + a 2 cos 4 j sin 2 j

dj = a cos 2 j dj .

r2 + (r¢)2

Тогда длина всей кривой

2 j

l = 2a ∫

cos

dj = a ∫

+ cos

dj =

= a j +

sin

ap (ед. длины).

2. У доски студенты решают задачи.

2.1.

Вычислить длину дуги кривой y = ln sin x от x

= p до x

Указание. Воспользоваться формулой

l =

∫ 1 + ( f ¢( x))2 dx =

∫ 1 + ( y¢)2 dx .

Ответ: 2ln 3 .

2.2.

x = a cos

Ответ: 6а ед. длины.

Найти длину астроиды

y = a sin 3 t.

( x¢(t ))2 + ( y¢(t ))2 dt ,

Указание. Воспользовавшись формулой l = ∫2

найдите в силу симметрии фигуры

длины кривой t Î 0;

2.3.Найти длину кардиоиды r = a (1 + cos j).

Указание. В силу симметрии фигуры найдите половину длины кри- вой jÎ[0;p] .

Ответ: 8а.

Обучающая задача 4. Найти длину петли кривой x = 3 t 2 , y = t - t 3 .

Решение. Найдем пределы интегрирования. Проведем анализ располо- жения кривой. Обе функции x (t ) и y (t ) определены при всех значениях t.

Так как функция x = 3t 2 ³ 0 , то кривая лежит в правой полуплоскости.

При изменении знака параметра t величина x (t ) не изменяется, а y (t ) меня-

ет знак. Значит, кривая симметрична относительно оси Ох. Кроме того,

129

функция x (t ) принимает одно и тоже значе-

ние не более чем два раза. Отсюда следует, что точки самопересечения кривой лежат на оси Ох, т. е. их можно определить из уравне-

ния у = 0 (рис. V.2).

На рисунке стрелками показано то на- правление, в котором текущая точка M ( x, y )

пробегает кривую при изменении t от −∞ до ∞ . Но у = 0 при t1 = 0 , t 2 = 1, t3 = −1. Так как x (t 2 ) = x (t3 ) = 3 , то точ-

ка (3;0) является единственной точкой самопересечения кривой. Следо-

вательно, мы должны интегрировать в пределах от t 2 = −1 до t3 = 1.

Дифференцируя параметрические уравнения кривой по t, получим

′	′	2
xt = 2 3 t ,	yt = 1 − 3t		, откуда


	( x′t )2 + ( y′t )2
dl =				dt = 12t 2 + 1 − 6t 2 + 9t 4 dt = 9t 4 + 6t 2 + 1 dt =

= (3t 2 + 1)2 dt = (3t 2 + 1)dt .

Следовательно,

1	(1 + 3t 2 )dt = (t + t 3 )	1−1
l = ∫			= 4 (ед. длины).
−1
−1

3. Вычисление объемов тел и площадей боковых поверхностей тел вращения. Рассмотреть вычисление объемов тел с помощью определенного интеграла.

10. Если площадь S ( x) сечения тела плоскостью, перпендикулярной к оси Ох, является непрерывной функцией на отрезке [a;b], то объем части

тела, заключенный между плоскостями x = a и x = b , перпендикулярными к оси Ох (рис.V.3), находится по формуле

V = b∫S ( x) dx .	(V.6)
a

20. Объем тела вращения, образо- ванного вращением вокруг оси Ох (или оси Оу) криволинейной трапеции, огра-

130

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 2513 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в папке Высшая математика (РТФ)

#
18.05.20152.77 Mб51умк_Вакульчик_Неопределенный интеграл.pdf
#
18.05.20153.63 Mб42умк_Вакульчик_Опред интеграл.pdf
#
18.05.20154.76 Mб40умк_Вакульчик_Элементы векторной алгебры.pdf
#
18.05.20155.38 Mб46умк_Вакульчик_Элементы линейной алгебры.pdf
#
18.05.20151.33 Mб47умк_Мальцев_Осн дискретной матем.pdf
#
18.05.20153.75 Mб53умк_Пальчик_Теория вероятностей.pdf
#
18.05.20155.68 Mб35умк_Цывис_Диф.уравнения_Ряды.pdf