Neutron Scattering in Biology - Fitter Gutberlet and Katsaras

458 H.D. Middendorf

nanotechnology, and the biosciences. If these aims will be realized, the future looks bright indeed!

Acknowledgments

I wish to thank colleagues at ISIS, ILL, PSI, KEK, and ANL for information and helpful comments on draft versions of this chapter. C. Corsaro, A. Deriu, M. Kataoka, C.K. Loong, S.F. Parker, K. Shibata, M.G. Taylor, and M.T.F. Telling kindly provided figures.

References

1.H.D. Middendorf, Annu. Rev. Biophys. Bioeng. 13 (1984), 425

2.M. B´ee, Quasielastic Neutron Scattering (Adam Hilger, Bristol, 1988)

3.P. Martel, Progr. Biophys. Mol. Biol. 57 (1992), 129

4.H.D. Middendorf, A. Miller, in Neutrons in Biology, B.P. Schoenborn, R.B. Knott (Eds.), (Plenum, New York, 1996), pp. 239–265

5.S. Cusack, H. B¨uttner, M. Ferrand, P. Langan, P. Timmins (Eds.), Biological Macromolecular Dynamics (Adenine Press, NewYork, 1997)

6.H.D. Middendorf, in Neutron Scattering from Novel Materials, A. Furrer (Ed.) (World Scientific, Singapore, 2000), pp. 141–158

7.F. Gabel, D. Bicout, U. Lehnert, M. Tehei, M. Weik, G. Zaccai, Qu. Rev. Biophys. 35 (2002), 327

8.H.D. Middendorf, R.L. Hayward, J. Neutron Res. 10 (2002), 123

9.N. Niimura, K. Shibata, H.D. Middendorf, J. Neutron Res. 10 (2002), 163

10.H.D. Middendorf, J. Neutron Res. 13 (2005), 79

11.C.G. Windsor, Pulsed Neutron Scattering (Taylor & Francis, London, 1981)

12.J. Newport, B.D. Rainford, R. Cywinski (Eds.), Neutron Scattering at a Pulsed Source (Adam Hilger, Bristol, 1988)

13.S. Ikeda, Appl. Phys. A 74 (2002), S15

14.T.E. Mason, R.K. Crawford, G.J. Bunick, A.E. Ekkebus, D. Belanger, Appl. Phys. A 74 (2002), S11

15.A. Taylor, Physica B 276–278 (2000), 36

16.F. Mezei, Neutron News 5 (1994), 2

17.B. Farago, in Time-of-Flight Neutron Spin Echo, in Neutron Spin Echo Spectroscopy, F. Mezei, C. Pappas, T. Gutberlet (Eds.) (Springer, Berlin, 2003)

18.C.J. Carlile, J. Penfold, Neutron News 6 (1995), 5

19.R.E. Lechner, Appl. Phys. A 74 (2002), S151

20.R. Bewley, R. Eccleston, Appl. Phys. A 74 (2002), S218

21.H.D. Middendorf, J. Phys. V-C3 France 5 (1995), 387; Physica B 226 (1996), 113

22.M.-C. Bellissent-Funel (Ed.): Hydration Processes in Biology (IOS Press, Amsterdam, 1999)

23.M.T.F. Telling, S.I. Campbell, D.D. Abbley, D.A. Cragg, J.J.P. Balchin, C.J. Carlile, Appl. Phys. A 74 (2002), S61

24.K. Shibata, I. Tamura, K. Soyama, M. Arai, H.D. Middendorf, N. Niimura, High E ciency Indirect Geometry Crystal Analyzer TOF Spectrometer: DYANA, in Proc. ICANS-XVI (ICANS-XVI, D¨usseldorf-Neuss, 2003)

25.C. Andreani, A. Filabozzi, F. Menzinger, A. Desideri, A. Deriu, D. DiCola, Biophys. J. 68 (1995), 2519

26.U.N. Wanderlingh, M. Cutroni, L. De Francesco, in Biological Macromolecular Dynamics, S. Cusack , H. B¨uttner, M. Ferrand, P. Langan, P. Timmins (Eds.) (Adenine Press, New York, 1997), pp. 171–174

27.C. Tengroth, L. B¨orjesson, W.W. Kagunya, H.D. Middendorf, Physica B 266 (1999), 27

28.L. Foucat, J.-P. Renou, C. Tengroth, S. Janssen, H.D. Middendorf, Appl. Phys. A 74 (2002), S1290

29.A. Deriu, F. Cavatorta, D. Cabrini, C.J. Carlile, H.D. Middendorf, Europhys. Lett. 24 (1993), 351

30.H.D. Middendorf, D. DiCola, F. Cavatorta, A. Deriu, C.J. Carlile, Biophys. Chem. 47 (1994), 145

31.A. Faraone, C. Branca, S. Magaz, G. Maisano, H.D. Middendorf, P. Migliardo, V. Villari, Physica B 276–278 (2000), 524

32.I. Ohmine, H. Tanaka, P.G. Wolynes, J. Chem. Phys. 89 (1998), 5852

33.H.E. Rorschach, D.W. Bearden, C.F. Hazlewood, D.B. Heidorn, R.M. Nicklow, Scanning Microscopy 1 (1987) 2043.

34.A. Deriu, Neutron News 11 (2000), 26

35.H.D. Middendorf, U.N. Wanderlingh, M.T.F. Telling, OSIRIS Exp. RB14292 (2004)

36.W. Doster, S. Cusack, W. Petry, Phys. Rev. Lett. 65 (1990), 1080

37.H. Nakagawa, H. Kamikubo, I. Tsukushi, T. Kanaya, M. Kataoka, J. Phys. Soc. Jap. 73 (2004), 491

38.D. Kern, E.R. Zuiderweg, Curr. Opin. Struct. Biol. 13 (2003), 748

39.H.D. Middendorf, Physica B 182 (1992), 415

40.Y. Izumi, K. Sakai, H. Oshino, M. Kataoka, Physica B 213–214 (1995), 772

41.M. Kataoka, M. Ferrand, A.V. Goupil-Lamy, H. Kamikubo, J. Yunoki, T. Oka, J.C. Smith, Physica B 266 (1999), 20

42.M. Kataoka, H. Kamikubo, J. Yunoki, F. Tokunaga, T. Kanaya, Y. Izumi, K. Shibata, J. Phys. Chem. Solids 60 (1999), 1285

43.M. Arai, Adv. Colloid Interface Sci. 71–72 (1997), 209

44.S.F. Parker, J. Neutron Res. 10 (2002), 173

45.S. Magaz`u, V. Villari, P. Migliardo, G. Maisano, M.T.F. Telling, H.D. Middendorf, Physica B 301 (2001), 130

46.C. Branca, S. Magaz`u, G. Maisano, S.M. Bennington, B. Fak,˙ J. Phys. Chem. B 107 (2003), 1444

47.F. Fillaux, J.P. Fontaine, M.-H. Baron, G. Kearley, J. Tomkinson, Chem. Phys. 176 (1993), 249

48.G.J. Kearley, F. Fillaux, M.H. Baron, S.M. Bennington, J. Tomkinson, Science 264 (1994), 1285

49.R.L. Hayward, H.D. Middendorf, U. Wanderlingh, J.C. Smith, J. Chem. Phys. 105 (1995), 5525

50.J. Baudry, R.L. Hayward, H.D. Middendorf, J.C. Smith, in Biological Macromolecular Dynamics, S. Cusack , H. B¨uttner, M. Ferrand, P. Langan, P. Timmins (Eds.) (Adenine Press, New York, 1997), pp. 46–49

460H.D. Middendorf

51.M.T.F. Telling, C. Corsaro, U.N. Wanderlingh, H.D. Middendorf, Eur. Biophys. J., (2005), submitted.

52.U.N. Wanderlingh, C. Corsaro, R.L. Hayward, M. B´ee, H.D. Middendorf, Chem. Phys. 292 (2002), 445

53.G.J. Kearley, Spectrochimica Acta 48A (1992), 349

54.J. Ulicny, M. Ghomi, H. Jobic, P. Miskovsky, A. Aamouche, J. Molec. Struct. 410 (1997), 497

55.G.J. Kearley, M.R. Johnson, M. Plazanet, E. Suard, J. Chem. Phys. 115 (2001), 2614

56.H.D. Middendorf, W. Montfrooij, S.M. Bennington, MARI Exp. RB5527 (unpubl. data).

57.M.G. Taylor, S.F. Parker, P.C.H. Mitchell, J. Molec. Struct. 651–653 (2003), 123

58.C.-K. Loong, C. Rey, L.T. Kuhn, C. Combes, Y. Wu, S.-H. Chen, M.J. Glimcher, Bone 26 (2000), 599

59.H.D. Middendorf, R.L. Hayward, S.F. Parker, J. Bradshaw, A. Miller, Biophys.

J.69 (1995), 660

60.F. Cavatorta, A. Deriu, N. Angelini, G. Albanese, Appl. Phys. A 74 (2002), S504

61.H.D. Middendorf, S.F. Parker, TFXA Exp. RB9726 (unpubl. data)

62.Z. Dhaouadi, et al., J. Phys. Chem. 97 (1993), 1074

63.M. Ghomi, A. Aamouche, H. Jobic, C. Coulombeau, O. Bouloussa, in Biological Macromolecular Dynamics, S. Cusack , H. B¨uttner, M. Ferrand, P. Langan,

P.Timmins (Eds.) (Adenine, New York, 1997), pp. 73–78

64.M.-P. Gaigeot, N. Leulliot, M. Ghomi, H. Jobic, C. Coulombeau, O. Bouloussa, Chem. Phys. 261 (2000), 217

65.M. Plazanet, N. Fukushima, M.R. Johnson, Chem. Phys. 280 (2002), 53

66.J. Mayers, Phys. Rev. B 41 (1991), 41; Phys. Rev. Lett. 71 (1993), 1553

67.R. Senesi, et al, Physica B 276 (2000), 200

68.U.N. Wanderlingh, A.L. Fielding, H.D. Middendorf, Physica B 241–243 (1998), 1169

69.H.D. Middendorf, R.L. Hayward, U.N.Wanderlingh, Nuovo Cimento 20 D (1998), 2215

70.U.N. Wanderlingh, F. Albergamo, R.L. Hayward, H.D. Middendorf, Appl. Physics A 74 (2002), S1283

71.A. Deriu et al, VESUVIO Exp. RB14697 (unpubl. data)

20

Brownian Oscillator Analysis of Molecular

Motions in Biomolecules

W. Doster

20.1 Introduction

Dynamic analysis of biomolecules often works by the principle of di erence spectroscopy: What is the qualitative di erence in structural flexibility of a protein with and without ligand? This method, illustrated elsewhere in this book, is quite useful considering the complexity of biomolecules. Sometimes, however, di erences between di erent samples are easier to obtain than reproducable identical results. This chapter is addressed to students of biophysics, who would like to proceed further. We present a modern statistical analysis of neutron scattering data applied to biomolecules. We start from the simple model of the harmonic oscillator, introduce the visco-elastic oscillator and conclude with a model-independent moment expansion of the density correlation function. To illustrate the method, a number of recent results on protein dynamics are presented. The power of neutron scattering is that it provides, both spectral and spatial, information from which one can reconstruct in principle the microscopic trajectory of labeled particles on a picosecond time scale. Such results can be used to test molecular dynamic simulations of biomolecules, and simulations can be used to interpret the neutron scattering spectra. Since protein–water interactions belong to the most interesting questions that can be approached with neutron scattering, we start with a brief outline on this topic.

20.2 Dynamics of Protein–Solvent Interactions

The nature of protein–solvent interactions is central to most basic questions in molecular biophysics ranging from protein folding, protein–ligand association to desease-related formation of protein aggregates. Biological structures owe their existence to a delicate balance of weak hydrophilic and hydrophobic forces, which are mediated by the solvent [1]. Moreover, proteins are dynamical structures, which undergo continuous thermal motion induced by the

462 W. Doster

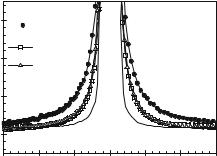
solvent. Dynamic neutron scattering experiments allow probing the protein– water fluctuations on the relevant time scales. In the absence of solvent or in a rigid environment functionally relevant motions are arrested. Water thus acts as a lubricant to protein dynamics. Figure 20.1 shows a neutron scattering spectrum of myoglobin, exposed to three types of environment: vacuum (dehydrated), fully hydrated with D2O (0.4 g g−1) and vitrified in a perdeuterated glucose glass [2].

The wings of the protein spectra appear to be broadened with respect to the resolution function, which is the signature of structural fluctuations on a picosecond time scale. It is obvious that the spectral broadening is more pronounced with the hydrated sample. The excess broadening derives from water-plasticized translational motions of side chains. That the spectra of the dehydrated and the glucose-vitrified protein display a finite and similar width, indicates rotational transitions of side chains, which persist irrespective of the protein environment. From a dynamical point of view, liquids and proteins are radically di erent, liquids exhibit short-range order and longrange translational di usion. Molecular displacements in liquids are continuous and isotropic. Proteins in contrast are long-range ordered, but molecular di usion is short-ranged. Internal displacements are discontinuous, rotational, and anisotropic. The protein–water interaction introduces liquid aspects to otherwise solid-like molecules. Molecular displacements in dense liquids are dominated by short-range repulsive interactions. For a molecule to move also requires that the nearest neighbors have to move. This is a collective phenomenon resembling more a continuous search for escape out of a cage rather than a discontinuous jump across an energetic barrier. By-passing the barrier by collecting su cient free volume instead of barrier crossing appears to be the dominant di usion mechanism in the liquid state [3]. The protein–water

Fig. 20.1. Neutron scattering spectra of di usive motions at Q = 1.9 ˚A−1 of myoglobin embedded in three environments as indicated (1 meV = 8 cm−1). Full line: instrumental resolution function (IN6, ILL). A vibrational background was subtracted

interaction causes the protein torsional barriers to fluctuate. The analysis of these motions by dynamic neutron scattering is a classical topic, which has been discussed by many authors, just to cite a small sample [4–6]. The relation between liquids and proteins was discussed in [7–11]. A recent review was published in [12]. The neutron scattering method has the particular advantage to probe the very low frequency range of a few terahertz, where vibrational and relaxational motions overlap. The corresponding spectral features cannot be assigned to vibrations of a particular group. Instead it is dominated by collective motions of many particles. To illustrate the application of neutron scattering to protein–water dynamics we follow a simple physical concept: Protein structural fluctuations are spatially constrained by covalent and van der Waals forces. As a general dynamic model of protein variables. we consider a set of harmonic oscillators which are driven by the random forces of a heat bath, which is essentially the solvent. The generalized protein coordinates Xα then obey a Langevin equation driven by the random forces Rα

We thus pick up the basic idea of a normal mode analysis of proteins, complemented by an appropriate frictional force [13,14]. Neutron scattering provides the tools to study the frictional force. In a dynamic neutron scattering experiment, the protein–water hydrogen atoms serve as a monitor to record the trajectory of the Xα in space and time. The theoretical aspects of the application of the Brownian oscillator model to neutron scattering has been discussed by Kneller [15].

20.3 Properties of the Intermediate Scattering Function

An insightful article on the neutron scattering process was written by Mezei [16]. Neutrons are scattered by the nuclei of the atoms, which are pointlike entities. The scattered beam pattern is thus determined by the superposition (interference) of spherical waves emitted by the individual atoms. The respective scattering amplitudes depend on the individual nuclear crosssections, which for C, N, O, H amount to σc = 5.5, 11.5, 4.2, and 1.76 b (1 b = 10−24 cm2), respectively [17]. The coherent cross-sections, which specify phase-preserving processes, contribute generally less than 10% to the total scattering intensity with protein samples. Three types of disorder generate an incoherent background (a) chemical disorder, neutron waves scattered by di erent types of atoms (N, C, H) or isotopes do not interfere; (b) positional disorder, protein powder samples or protein solutions are rotationally disordered, thus waves scattered by identical atoms in di erent proteins exhibit a random phase relationship; and (c) spin disorder, the neutron cross-section of hydrogen fluctuates depending on whether the respective neutron–proton spins are parallel or antiparallel. The spin-disorder in combination with the

464 W. Doster

negative scattering length of the proton, lead to a large incoherent crosssection, σinc = 80.2 b [17]. Therefore, roughly 90% of the combined scattering cross-section of D2O-hydrated protein samples is incoherent. The scattering function Sinc(Q, ω) thus should be interpreted as the sum of intensities and not as a square of the sum of amplitudes. Finally only those waves can interfere, which originate from one and the same hydrogen atom. This is called “selfinterference” and refers to the average behavior of single particles: The motion of the hydrogen atom modulates the phase of the scattered wave (Doppler shift). The selfscattering trace in time thus reflects the trajectory of individual particles. The coherent fraction corresponds to relative displacements of two distinct atoms. Single particle motions are generally easier to interpret than the relative motion of two distinct particles. One can thus derive most of the relevant dynamical information from incoherent scattering, which has the further advantage to be much more intense. Dynamic analysis of coherent scattering is important with perdeuterated proteins or solutions with D2O. The neutron scattering experiment determines the statistical average of the phase factors at di erent times.

This is the self-intermediate scattering function Is,i(Q, t) defined for each atom (i ) by

We omit the cross-sections, since we consider a system of hydrogen atoms, dominating the scattering intensity. The scattering vector Q is an adjustable parameter, which allows to modify the spatial scale probed by the scattering process. Q = 4π/λn sin(θ/2) defines its length, λn denotes the wavelength of the incident neutrons, and θ is the scattering angle. I(Q, t) can be expressed as the Fourier transform of the van Hove self-correlation function in space,

This even function in space (and time) [17] describes the single particle dynamics of a system averaged over the possible starting points in space. It denotes the probability density, that atom (i ) which is initially at r0 moves to a position r within a time interval t. For a classical system it can be written as

Thus the Q-dependence of Is,i(Q, tres) contains the complete information about the single particle dynamics at any fixed instant of time t = tres (often defined by the energy resolution of the instrument). This argument is stressed because the intermediate scattering function is usually introduced as a correlation function versus time or spectrum versus frequency.

466 W. Doster

– The intermediate scattering function and dynamic structure factor factor-

all atoms. S(Q, ω) denotes the so-called dynamical structure factor, which is the quantity determined by most spectrometers (time-of-flight and backscattering). It is obtained from constant angle cuts at fixed frequency and involves interpolation (see below). The intermediate scattering function is then derived

by numerically transforming S(Q, ω) to the time domain

I(Q, t) = S(Q, ω) exp(iωt)d( ω). (20.12)

If the inequality of Eq. 20.8 holds up to a certain time tmax, then the Fourier transform is only valid in the set of discrete points

Note also that the measured linewidth of a localized process with time constant τloc less than tmax, i.e.,

is independent of Q and is given by its actual value Γloc = 1/τloc. In addition the squared amplitude of such a process is directly given by the integral over the corresponding quasielastic spectrum. A localized motion or glassy state leads to a long-time plateau of the intermediate scattering function, EISF(Q) = I(Q, t → ∞), the so-called elastic incoherent structure factor. Then a purely elastic component (δ-function) arises in S(Q, ω) at ω = 0. The EISF(Q) is the Fourier transform of the displacement distribution G(r, t → ∞). A finite elastic fraction also obtains, if the correlations do not vanish within the time defined by the energy resolution of the spectrometer.

With Eqs. 20.4 and 20.5 one obtains the useful relation

EISF(Q) =| dr · exp(iQr) · p(r − r0) |2 . (20.15)

The elastic fraction, EISF(Q), thus represents the orientationally averaged (single particle) displacement distribution at infinite time.

1Let us – for notational simplicity – assume the usual case of an isotropic sample (not necessarily isotropic dynamics!, see below) which leads to the orientational average of the scalar products in the displacement moments