
sotsiologia
.pdf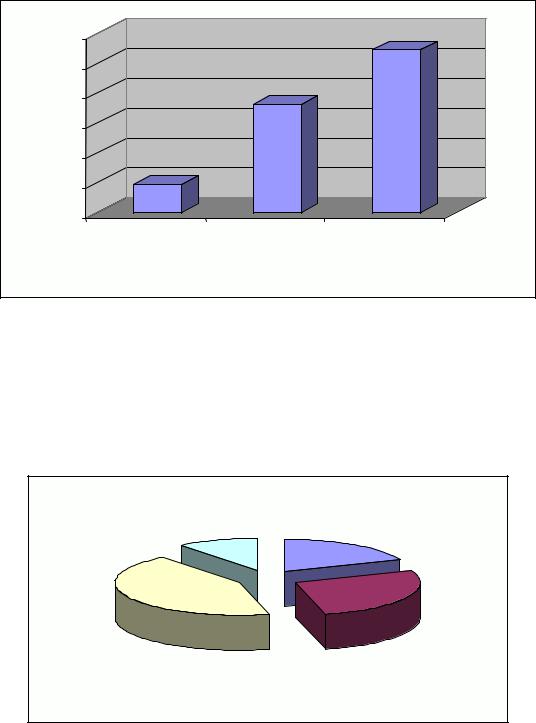
60 % |
|
|
50 % |
|
|
40 % |
|
|
30 % |
|
|
20 % |
|
|
10 % |
|
|
0 % |
|
Высшее |
Среднее общее |
Среднее |
|
|
профессиональное |
|
Рис. 1. Распределение респондентов по уровню образования |
||
Одного общего взгляда на эту диаграмму достаточно, чтобы оценить соотношение численности опрошенных с разным уровнем образования.
На рис. 2 мы видим другую форму графического представления данных. Здесь приведена круговая диаграмма, иллюстрирующая распределение предпочтений, отдаваемых различным учебным дисциплинам.
Математика |
Маркетинг |
Английский |
Социология |
|
язык |
||
|
Рис. 2. Распределение предпочтений, отдаваемых различным учебным дисциплинам
Для данных номинального уровня возможны следующие статистические расчеты: абсолютная частота, процентные отношения, мода.
Мода (модальная категория) – величина признака, которая встречается в изучаемой совокупности чаще, чем другие величины данного признака. Например, если в выборке содержится 60 % православных, 30 % мусульман и 10 % представителей других конфессий, то модальным значени-
150

ем будет «православный». В табл. 1 модельную категорию составляют женщины.
Но у моды как способа показать наиболее типичное, распространенное значение есть определенные недостатки, ограничивающие ее интерпретацию:
–в распределении могут быть две и более моды(соответственно оно является бимодальным или мультимодальным). Например, если в группе из десяти человек четверо не имеют автомобиля (0), четверо имеют один автомобиль (1), один человек имеет две машины и еще один – три, то нам придется указать два модельных значения – «0» и «1»;
–мода чрезвычайно чувствительна к способу группировки значений переменной (то есть классификации, упорядочиванию данных по какомулибо признаку). Объединяя категории ответа, мы резко увеличиваем число наблюдений в отдельных категориях, это открывает широкий простор для манипулирования данными;
–сложно определить моду(и лучше воздержаться от ее вычисления) в том случае, когда частоты для всех наблюдаемых значений почти равны. Например, 48 % болельщиков поддерживают сборную Италии, а
49 % – сборную Бразилии, модальное значение «поддерживает бразильцев» будет не очень модальным1.
И все же во многих случаях вычисление моды и необходимо, полезно. Например, для архитектора, занимающегося планированием жилых домов, знание модального значения жилой площади для размера семьи в данной местности может оказаться весьма важным.
В принципе, та же одномерная статистика, что используется для суммирования данных номинального уровня, может быть применена и для данных рангового уровня. Здесь методы описательной статистки более информативны, для измерений порядкового уровня типичное значение частотного распределения можно выявить с помощью как моды, так и медианы.
Медиана – величина варьирующего признака, делящая совокупность на две равные части, со значениями больше и меньше медианы. Медиану иногда называют «позиционным средним», так как она указывает именно среднюю позицию в упорядоченном ряду наблюдений. Медиана может совпадать или не совпадать с модой.
Можно посмотреть, как определяется медиана на примере распределения ответов на вопрос о том, какова частота использования различных источников информации о работе городской администрации (табл. 3.).
1 См.: Девятко И. Ф. Методы социологического исследования. – М., 2006. – С. 241–242.
151

|
|
|
|
|
|
Таблица 3 |
Источники информации о работе городской администрации |
|
|||||
|
|
|
|
|
|
|
Источники информации |
|
|
Частота / ранг |
|
|
|
Часто |
РегулярноИногда |
|
Никогда |
Не дали |
||
|
|
|
|
|
|
ответа |
|
4 |
3 |
2 |
|
1 |
0 |
Встречи с мэром |
2 |
5 |
39 |
|
282 |
98 |
и работниками |
|
|
|
|
|
|
администрации города |
|
|
|
|
|
|
Городские газеты |
46 |
76 |
171 |
|
71 |
62 |
Общение с коллегами |
30 |
63 |
124 |
|
104 |
105 |
по работе |
|
|
|
|
|
|
Общение с родными, |
45 |
82 |
167 |
|
52 |
80 |
соседями, друзьями |
|
|
|
|
|
|
Радио |
66 |
88 |
142 |
|
64 |
66 |
Телевидение |
133 |
129 |
121 |
|
22 |
21 |
Здесь значения переменных – частоты использования того или иного источника – соотнесены с ранговой шкалой, значения которой меняются от категории «часто» (которой присвоен ранг 4) до «не дали ответа» (ранг 0). С учетом того, что общее число опрошенных (или число наблюдений) равно 426, половина наблюдений составит 213. Это означает, что медиана для такого источника информации, как «встречи с мэром и работниками администрации города» приходится на категорию с рангом1 (никогда); для четырех последующих переменных: «газеты», «коллеги», «семья», «радио» – на категорию с рангом 2 (иногда); для последней переменной – «телевидение» – медиана приходится на категорию 3 (регулярно).
Отметим, что при использовании для измерений порядкового уровня методы описательной статистики более информативны, нежели для измерений номинального уровня.
Для того чтобы полученную числовую информацию можно было представить обобщенно, а также выявить типичные характеристики совокупности, рассчитывают средние величины – это обобщающие показатели.
Их можно рассчитывать по количественным и по качественным признакам. Например, средний возраст сотрудников фирмы, средний стаж работы, средняя заработная плата и .т п., а также типичный для большинства группы мотив получения образования, смены профессии или уровень удовлетворенности работой и т. д.
Важнейшим условием применения средних величин является их расчет на качественно однородной совокупности. Это требование предполагает, например, что мы не будем с целью выявления покупательной способ-
152

ности типичного работника предприятия усреднять заработную плату администрации и низовых работников, размеры которой сильно различаются.
В статистическом анализе применяются различные виды средних величин. Так, достаточно часто используют среднюю арифметическую про-
стую и среднюю арифметическую взвешенную. Вторая применяется, если имеется некоторая повторяемость значений единиц совокупности, и рассчитывается она по формуле
х = å х i n i ,
å n i
где хi – значение показателя, ni – частота (повторяемость признака). Средняя величина рассчитывается не только для количественных при-
знаков, но и для качественных, выраженных в порядковых шкалах. Для определения средних значений строятся индексы. Например, индекс удовлетворенности студентов учебой можно рассчитывать по 5-членной шкале (табл. 4).
|
|
|
|
|
|
Таблица 4 |
||
|
Степень удовлетворенности студентов учебой |
|||||||
|
|
|
|
|
|
|
|
|
Ответ |
|
Частота |
|
Процент |
||||
|
|
|
|
|
|
|
|
|
Да |
|
55 |
|
|
30,0 |
|
||
Скорее да, чем нет |
|
60 |
|
|
32,8 |
|
||
Ни да, ни нет |
|
32 |
|
|
17,5 |
|
||
Скорее нет, чем да |
|
21 |
|
|
11,5 |
|
||
Нет |
|
15 |
|
|
8,2 |
|
||
Итого |
|
183 |
|
|
100,0 |
|
||
Индекс рассчитывается по формуле |
|
|
||||||
I = |
a + 0,5b - 0,5 d - f |
или I = |
n1 + 0,5n 2 |
- 0,5n 4 - n 5 |
, |
|||
a + b + c + d + f |
||||||||
|
|
|||||||
|
|
|
å ni |
|||||
где a, b, c, d, f – пункты порядковой шкалы.
Смысл расчета данного индекса заключается в том, чтобы увидеть, каково соотношение положительных и отрицательных пунктов шкалы. Так, в нашем примере числитель представляет собой разницу между позитивным (85) и негативным (25,5) отношением студентов к учебе.
Индекс нормирован, то есть он изменяется в границах от+1 до –1, где «+1» означает, что все респонденты удовлетворены учебой, «–1» – о полной неудовлетворенности опрошенных.
153

Для 3-членной шкалы данную формулу нужно упростить, то есть от суммы положительных ответов отнять сумму отрицательных и полученный результат разделить на количество опрошенных:
n+ - n-
I = n+ + n0 + n- ,
где n+, n0, n– – положительные, нейтральные и отрицательные значения порядковой шкалы.
Измерения интервального и пропорционального уровней редко ана-
лизируются с помощью прямого указания частот или процентных отношений. Критериями центральной (типичной) тенденции измерений выступают мода, медиана и среднее арифметическое.
Среднее арифметическое – сумма значений переменной, поделенная на число значений. Общая формула для ее вычисления алгебраически выглядит следующим образом:
|
х |
= åхi |
= |
x1 + x2 +... + xi |
, |
|
|
||||
|
|
N |
|
N |
|
где хi – числовое значение i-й |
позиции, а N – общее число наблюдений |
||||
(объем выборки). |
|
|
|
||
Рассмотрим вычисление средней арифметической величины на примере расчета средней посещаемости занятий в студенческой группе по данными проверок деканата. Данные о посещаемости приведены в табл. 5.
Таблица 5
|
Посещаемость занятий студентами |
|
|
|
|
Номер занятия |
|
Число присутствующих |
|
|
|
1 |
|
17 |
2 |
|
21 |
3 |
|
18 |
4 |
|
14 |
5 |
|
20 |
6 |
|
20 |
7 |
|
16 |
8 |
|
17 |
9 |
|
21 |
10 |
|
22 |
Сложив числа в правой колонке и разделив их на10 (число проверок), мы получим, что средняя посещаемость в группе составила18,6. По-
нятно, что полученное число не может иметь реального физического смысла, оно пригодится лишь для сравнения уровня посещаемости в двух
154

группах и более. Хотя и для этой цели полученные величины вначале следует нормировать, разделив их на общую численность студентов каждой группы.
Вычисление средней арифметической величины для переменных, значения которых измеряются не однозначно определенными числами, изменяются вдоль непрерывного ряда значений, имеет свои особенности. Здесь рассчитывается не среднее арифметическое, средневзвешенное. Формула для средневзвешенного значения выглядит следующим образом:
х = åхi = х1n1 +х2n2 +...+хini ,
N N
где хi – числовое значение i-й позиции, ni – число респондентов, наблюдаемых по i-й позиции, а N – общее число наблюдений (объем выборки).
Предположим, что нам требуется вычислить средний возраст опрошенных респондентов (табл. 6).
|
Распределение респондентов по возрасту |
Таблица 6 |
||
|
|
|||
|
|
|
|
|
Возраст, |
Частота |
Процент |
Середина интервала |
niхi |
лет |
ni |
|
хi |
|
18–24 |
46 |
10,1 |
21 |
966 |
25–29 |
55 |
12,0 |
27 |
1485 |
30–39 |
97 |
21,2 |
34,5 |
3346,5 |
40–49 |
115 |
25,2 |
44,5 |
5117,5 |
50–59 |
74 |
16,2 |
54,5 |
4033 |
60–70 |
70 |
15,3 |
65 |
4550 |
Итого |
457 |
100,0 |
∑ |
19 498 |
Вначале мы должны определить середину каждого интервалахi. Это делается путем вычисления простого среднего, то есть сумма крайних значений делится пополам. Затем необходимо умножить это значение на число респондентов соответствующего возрастаniхi, сложить полученные произведения и разделить на общий объем выборки. В результате мы получим средний возраст в 42,6 года.
Показатели разброса данных интервального уровня включают в себя среднее отклонение, дисперсию и среднеквадратическое отклонение.
Среднее отклонение – мера разброса, основанная на отклонении каждого из значений от среднего. Хотя среднее отклонение и выявляет разброс, чаще для его измерения используются дисперсия и среднеквадратическое отклонение.
Дисперсия (от англ. dispersion – разбрасывание, рассеивание) – это рассеяние реально полученных данных вокруг среднего значения. Рассчитается следующим образом:
155

σ 2 = å ( х i - х ) 2 .
N
Среднеквадратическое отклонение представляет собою корень квад-
ратный из дисперсии:
S = 
 å ( хi - х )2 .
å ( хi - х )2 .
N
2
Чем больше разброс данных вокруг среднего, тем выше значения σ и S. Это означает, что если все данные одинаковы, то σ2 и S равны нулю. В зависимости от того, какова дисперсия, мы можем судить, насколько единодушны были в своих оценках респонденты(при меньшем значении дисперсии), или наоборот – насколько сильно они расходятся в своих мнениях (при большем значении дисперсии).
Описанные процедуры анализа одномерного распределения относятся к дескриптивной статистике, но если мы хотим обобщить данные, полученные на отдельных выборках, чтобы описать свойства исходной генеральной совокупности, необходимо обратиться к методам индуктивной статистики, к теории статистического вывода. Переход от числовых характеристик выборки к числовым характеристикам генеральной совокупности называется оцениванием. При одномерном анализе данных чаще всего решают задачу интервального оценивания.
Анализ двумерных распределений (парных распределений)
Хотя результаты одномерного анализа данных часто имеют самостоятельное значение, большинство исследователей уделяют основное внимание анализу связей между переменными. Самым простым и типичным является случай анализа взаимосвязи двух переменных.
Двумерные таблицы расширяют аналитические возможности исследования. Они строятся на основе группировки данных по двум признакам
иявляются основой для выявления взаимосвязей между признаками.
Вгипотезе, как правило, высказывается предположение о наличии связи между двумя и более переменными. С помощью анализа парных распределений мы можем определить, существует ли такая связь, каково ее направление, насколько она сильная, является ли она статистически значимой.
Предположим, мы сформулировали гипотезу: «Чем старше избиратели, тем больше вероятность того, что они примут участие в выборах».
При обработке данных опроса нам необходимо сопоставить значения независимой переменной (возраст респондентов) с соответствующими им
156
значениями зависимой переменной (электоральная активность: участие или неучастие в выборах). С целью сопоставления мы составляем таблицу сопряженности или парного распределения (табл. 7).
|
|
|
|
|
|
|
Таблица 7 |
|
Участие в выборах избирателей различных возрастов |
|
|||||
|
|
(в % от числа ответивших, N = 500) |
|
|
|||
|
|
|
|
|
|
|
|
Возраст |
|
|
Участие в голосовании |
|
Всего |
||
респондентов |
|
|
|
|
|
||
Да |
Нет |
Не помнят |
|
Нет ответа |
|||
|
|
|
|
||||
18–24 |
|
34,8 |
58,7 |
6,5 |
|
0,0 |
100,0 |
25–29 |
|
54,5 |
32,7 |
12,7 |
|
0,0 |
100,0 |
30-39 |
|
59,8 |
27,8 |
9,3 |
|
3,1 |
100,0 |
40–49 |
|
65,2 |
27,8 |
6,1 |
|
0,9 |
100,0 |
50–59 |
|
64,9 |
27,0 |
8,1 |
|
0,0 |
100,0 |
60–70 |
|
70,0 |
25,7 |
4,3 |
|
0,0 |
100,0 |
Старше 70 |
|
58,1 |
30,2 |
7,0 |
|
4,7 |
100,0 |
Так как вывод о наличии взаимосвязи между переменными требует демонстрации различий между подгруппами по уровню зависимой переменной, при анализе таблицы сопряженности можно руководствоваться простыми правилами. Во-первых, нужно определить независимую переменную и в соответствии с принятым определением рассчитать проценты. Если независимая переменная расположена по горизонтали таблицы, мы считаем проценты по столбцу; если независимая переменная расположена по вертикали, проценты берутся от сумм по строке. Во-вторых, сравниваются процентные показатели, полученные для подгрупп с разным уровнем независимой переменной, каждый раз внутри одной категории независимой переменной (например, в категории участвовавших в голосовании). Обнаруженные различия свидетельствуют о существовании взаимосвязи между двумя переменными.
Анализ проводят, отслеживая изменения значений зависимой переменной при переходе ее от одного значения к другому. Процедуру отслеживания можно проводить как по строкам, так и по столбцам. Это позволяет нам сделать выводы:
–о наличии связи между переменными(существует отчетливо выраженная связь между возрастом избирателей и их электоральной активностью);
–направлении этой связи, которая в данном случае является прямой (положительной), поскольку ее можно выразить следующим простым описанием: чем больше возраст, тем выше процент участия представителей этой возрастной группы в голосовании.
Понятие силы связи имеет отношение к тому, насколько существенно различаются наблюдаемые значения зависимой переменной при измене-
157
нии значений независимой переменной. Предположим, что характер голосования одной категории избирателей(к примеру, мужчин) значительно отличается от характера голосования другой категории(женщин), тогда мы можем утверждать, что имеет место сильная связь между двумя переменными. Если степень различия в характере их голосования мала, имеет место слабая связь.
Довольно часто используемым показателем силы связи выступают различные коэффициенты корреляции. Корреляция (от англ. correlation – связь, соотношение) указывает на степень статистической взаимосвязи признаков. Рассмотрим некоторые из них.
Коэффициент Юла [–1, +1] – как мера близости рассчитывается для дихотомических признаков (4-клеточных таблиц 2 х 2). Вне зависимости от знака «1» означает наличие явно выраженной связи между признаками,
а «0» – отсутствие таковой. Оценка значимости осуществляется по критерию χ2.
Для номинальных шкал рассчитывается хи-квадрат (гипотеза о статистической независимости, если 0,05 – то зависимости нет). Коэффициент Крамера [0, +1] – значимость определяется значимостью связи по критерию «хи-квадрат»: если χ2 значим, то и коэффициент значим.
Среди ранговых коэффициентов корреляции наиболее простым для расчета является коэффициент Спирмена [–1, +1] – он используется для определения тесноты связи между признаками, значения которых можно проранжировать. Коэффициент Спирмена, равный «+1», означает полную идентичность в ранжировании двух сравниваемых признаков, а равный «– 1» – ранжирование признаков у двух сравниваемых групп прямо противоположно.
Строго говоря, коэффициент ранговой корреляции показывает, насколько одинаковыми или различными оказываются ответы на один и тот же вопрос со стороны двух сравниваемых между собой групп респондентов.
Для выявления связи между количественными переменными вычисляется коэффициент Пирсона [–1, +1] – коэффициент, равный «0», означает отсутствие связи между признаками. Знак при коэффициенте указывает на направление связи. Так, значения «+1» и «–1» показывают наличие прямой и обратной связи между признаками. Чем ближе значение коэффициента к «1», тем теснее эта связь.
Обнаружив наличие взаимосвязи между двумя переменными и оценив интенсивность этой связи с помощью какого-нибудь коэффициента, социолог стремится проинтерпретировать эту связь в терминах причин и следствий. Однако само по себе наличие связи между двумя переменными еще не доказывает, что эта связь может быть описана моделью«причина– следствие» (например, существует сильная взаимосвязь между престижностью учебного заведения, где было получено образование, и престижностью работы), а нулевой коэффициент сопряженности – еще не свидетель-
158
ство отсутствия всякой причинной зависимости. Учитывая эти обстоятельства, многие исследователи используют несколько более сложные статистические методы анализа, свободные от ограничений.
Контрольные вопросы
1.Что собой представляет анализ данных?
2.Какие методы анализа данных можно выделить? В чем их особен-
ность?
3.Что такое кодирование информации и какие требования к нему предъявляются?
4.Какие статистические расчеты возможны при номинальном, порядковом и интервальном измерении?
5.Что такое средние величины? Какие правила необходимо соблюдать при их расчете?
6.Для каких показателей можно рассчитывать средние величины?
7.Как можно определить силу связи между признаками?
8.Какие виды средних величин используются в анализе данных?
9.Что такое корреляция?
10.Каковы основные показатели направления и силы связи?
159
