
- •Вычисление определителей 2-го, 3-го и высших порядков
- •1. Определитель 2-го и 3-го порядков.
- •2. Определитель произвольного порядка.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Действия над матрицами, вычисление обратной матрицы. Решение матричных уравнений
- •1. Алгебра матриц.
- •2. Обратная матрица.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Решение систем линейных уравнений методом Крамера и Гаусса
- •1. Метод Крамера.
- •2. Метод Гаусса.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Векторная алгебра. Вычисление координат, модуля и направляющих косинусов вектора
- •1. Векторная алгебра.
- •2. Деление отрезка в данном отношении.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Скалярное, векторное и смешанное произведения векторов
- •1. Скалярное произведение векторов.
- •2. Векторное произведение векторов.
- •3. Смешанное произведение векторов.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Прямая линия на плоскости
- •1. Общее уравнение прямой.
- •2. Уравнение прямой в отрезках.
- •3. Каноническое уравнение прямой.
- •6. Параметрические уравнения прямой.
- •7. Прямая с угловым коэффициентом.
- •8. Нормальное уравнение прямой.
- •10. Условия параллельности и перпендикулярности прямых. Нахождение угла между прямыми.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Плоскость и прямая в пространстве
- •1. Общее уравнение плоскости.
- •2. Уравнение плоскости в отрезках.
- •3. Уравнение плоскости, проходящей через три точки, не лежащие на одной прямой.
- •5. Уравнение плоскости, параллельной двум неколлинеарным векторам и проходящей через точку.
- •7. Нормальное уравнение плоскости.
- •9. Общие уравнения прямой.
- •10. Канонические уравнения прямой.
- •12. Параметрические уравнения прямой.
- •13. Взаимное расположение прямых и плоскостей.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Кривые второго порядка
- •1. Эллипс.
- •2. Гипербола.
- •3. Парабола.
- •4. Единое определение кривой второго порядка.
- •5. Полярное уравнение кривой второго порядка.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Предел числовой последовательности. Предел функции
- •1. Предел числовой последовательности.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Раскрытие неопределенностей. Замечательные пределы
- •1. Замечательные пределы.
- •2. Сравнение бесконечно малых.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Непрерывность функции. Точки разрыва функции
- •1. Непрерывность функции.
- •2. Точки разрыва.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Вычисление производных
- •1. Производная и ее геометрический и механический смысл.
- •3. Производные основных элементарных функций.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Производная неявной, параметрически заданной и сложно-степенной функции
- •Задачи для самостоятельного решения
- •Производные высших порядков. Дифференциал функции. Приложения дифференциалов
- •1. Производные высших порядков.
- •2. Дифференциал функции.
- •3. Формула приближенного вычисления.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Правило Лопиталя. Точки экстремума функции.
- •1. Правило Лопиталя.
- •2. Возрастание и убывание функции.
- •3. Точки экстремума функции.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Исследование функций и построение графиков
- •1. Выпуклость и вогнутость функции.
- •2. Точки перегиба функции.
- •3. Асимптоты функции.
- •4. Общий план исследования функции и построение графика.
- •Примеры решения задач
- •Задачи для самостоятельного решения
Примеры решения задач
1. Составить уравнение прямой линии, отсекающей на оси ординат отрезок, величина которого равна 2 , и наклонённой к оси абсцисс под углом в 45°.
Решение: Здесь b = 2 и k = tg45° = 1. Следовательно, используя (6.7), получаем уравнение у = х + 2.
2. Написать уравнение с угловым коэффициентом для прямой линии, заданной уравнением 2х + 3у + 7 = 0.
Решение: Разрешив данное уравнение относительно у, получим:
у
=
–![]() х
–
х
–
![]() .
.
Отсюда
следует, что угловой коэффициент прямой
k
= –![]() ,
а величина отрезка, отсекаемого ею на
оси ординат,b
= –
,
а величина отрезка, отсекаемого ею на
оси ординат,b
= –![]() .
.
3. Составить уравнение прямой, проходящей через точку (–3; 4) и наклонённой к оси Ох под углом в 135°.
Решение:
Используем (6.8). Здесь х![]() =
–3, у
=
–3, у![]() = 4, k
= tg135°
= –1. Следовательно, искомое уравнение
будет
= 4, k
= tg135°
= –1. Следовательно, искомое уравнение
будет
у – 4 = –1 ( х + 3 ),
или
х + у – 1 = 0.
4.
Составить уравнение прямой линии,
проходящей через точки М ![]() иN(2;1).
иN(2;1).
Решение:
Составим уравнение прямой линии по двум
точкам
![]() и (2;1) (формула (6.4)). Искомое уравнение
будет
и (2;1) (формула (6.4)). Искомое уравнение
будет![]() =
=![]() ,
или
,
или![]() =
=![]() ,
или
,
или![]() =
=![]() ,
откуда 5у
–
,
откуда 5у
–
![]() = –х
–
= –х
–![]() ,
илих
+
5у
–
7 = 0.
,
илих
+
5у
–
7 = 0.
5. Уравнение прямой 2х – 3у + 2 = 0 написать в отрезках.
Решение: Перенося свободный член данного уравнения в правую часть равенства, получим:
2х – 3у = –2.
Разделив обе части равенства на –2, будем иметь:
–![]() +
+
![]() = 1, или
= 1, или![]() +
+![]() = 1.
= 1.
6. Уравнение прямой линии 3х – 4у – 5 = 0 привести к нормальному виду.
Решение:
Нормирующий множитель равен: μ =
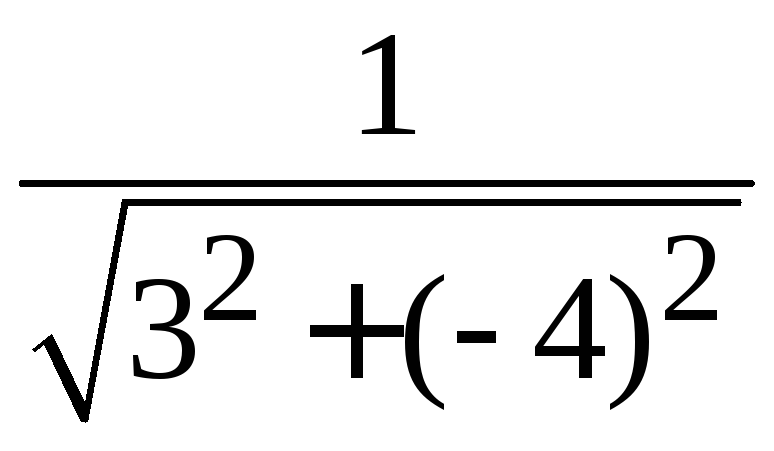 =
=![]() .
Умножая на него данное уравнение,
получим:
.
Умножая на него данное уравнение,
получим:
![]() х
–
х
–![]() у
– 1 = 0.
у
– 1 = 0.
Для
данной прямой имеем: p
= 1, cosα
=
![]() ,sinα
= –
,sinα
= –
![]() .
.
7. Найти угол между прямыми у = 2х – 3 и 3х + у – 2 = 0.
Решение:
Воспользуемся формулой (6.18). Пусть k![]() –
угловой коэффициент прямой у = 2х – 3,
k
–
угловой коэффициент прямой у = 2х – 3,
k![]() = 2,
k
= 2,
k![]() – угловой коэффициент прямой
3х
+
у
–
2 = 0, k
– угловой коэффициент прямой
3х
+
у
–
2 = 0, k![]() = –3. Тогда tgφ
=
= –3. Тогда tgφ
=![]() = 1, откуда φ = 45°.
= 1, откуда φ = 45°.
 8.
Найти уравнения двух прямых, проходящих
через точку М0(1;4),
если одна перпендикулярна, а другая
параллельна прямой l,
заданной уравнением x
– 2y
+ 4 = 0.
8.
Найти уравнения двух прямых, проходящих
через точку М0(1;4),
если одна перпендикулярна, а другая
параллельна прямой l,
заданной уравнением x
– 2y
+ 4 = 0.
Решение:
Обозначим
![]() и
и![]() прямые, первая из которых параллельна,
а вторая перпендикулярна прямой
прямые, первая из которых параллельна,
а вторая перпендикулярна прямой![]() .
Вектор нормали
.
Вектор нормали![]() = (1; –2) является нормалью к прямой
= (1; –2) является нормалью к прямой![]() и направляющим вектором к прямой
и направляющим вектором к прямой![]() .
.
Воспользуемся
формулой (6.5):
![]() илиx
– 2y
+ 7 = 0.
илиx
– 2y
+ 7 = 0.
Далее
воспользуемся формулой (6.3):
![]() или
2х + у –
6 = 0.
или
2х + у –
6 = 0.
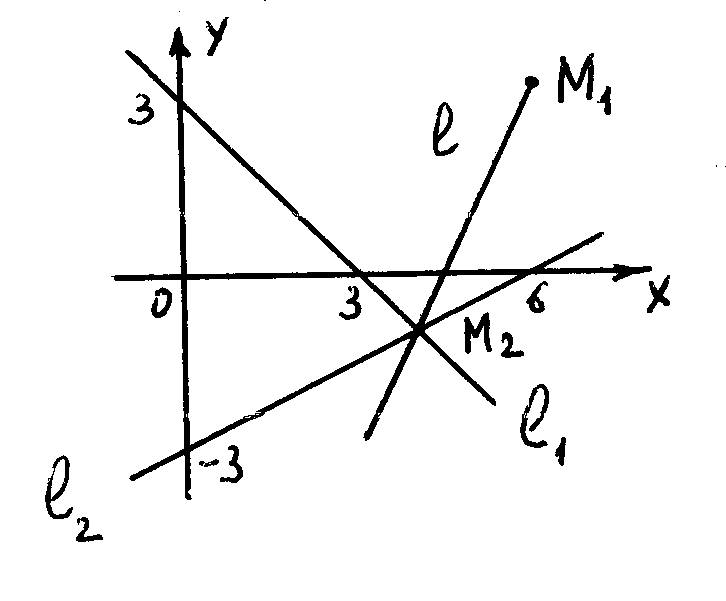
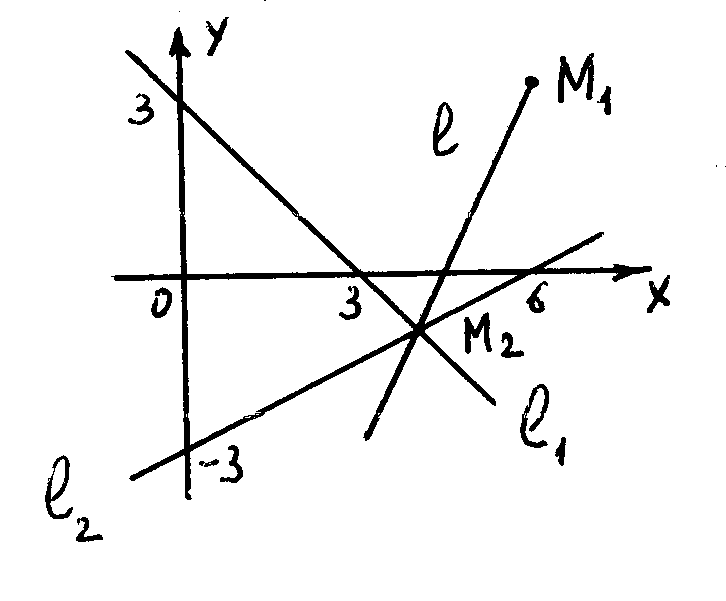
8.
Составить уравнение прямой l,
проходящей через точку М![]() (6;
4) и точку пересечения прямых х
+ у
– 3 = 0, х
– 2у
– 6 = 0.
(6;
4) и точку пересечения прямых х
+ у
– 3 = 0, х
– 2у
– 6 = 0.
Решение:
Координаты точки пересечения дает
решение системы уравнений: Решая эту систему, находимМ
Решая эту систему, находимМ![]() (4;
–1). Имеем координаты двух точек и
используем формулу (6.4). Получаем
(4;
–1). Имеем координаты двух точек и
используем формулу (6.4). Получаем
![]() или
5х
– 2у
– 20 = 0.
или
5х
– 2у
– 20 = 0.
9.
Найти расстояние между параллельными
прямыми l![]() :
3x
– y
+ 2 = 0 и l
:
3x
– y
+ 2 = 0 и l![]() :
6x
– 2y
– 7 = 0.
:
6x
– 2y
– 7 = 0.
Решение:
Выберем произвольную точку на l1.
Пусть x
= 0, тогда у
= 2 или М0(0;
2). Расстояние между прямыми
![]() и
и![]() – это и будет расстояние от точкиМ0(0;
2) до прямой
– это и будет расстояние от точкиМ0(0;
2) до прямой
![]() .
Воспользуемся формулой (6.10):
.
Воспользуемся формулой (6.10):
d
=
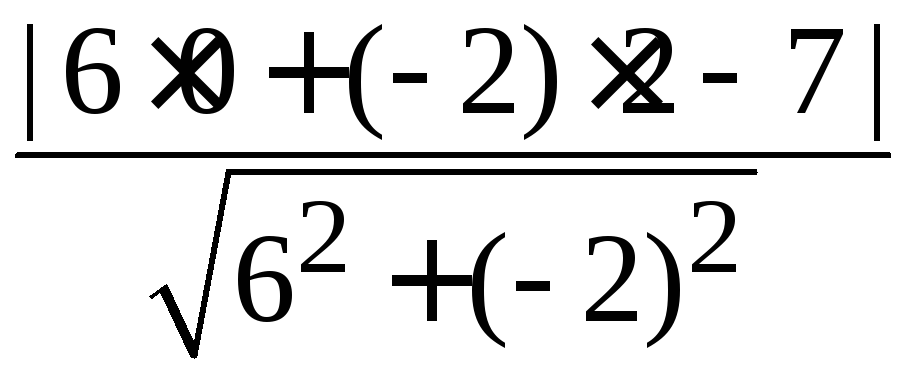 =
=
![]() .
.
10. Даны вершины ABC: A(2; 1), B(–1; –1), C(3; 2). Составить уравнение высоты AM.
Решение:
Запишем уравнение прямой, проходящей
через две точки B
и C,
используя формулу (6.4), получаем
![]() илиВС:
3x
– 4y
– 1 = 0, т.е. угловой коэффициент прямой
ВС
будет k
илиВС:
3x
– 4y
– 1 = 0, т.е. угловой коэффициент прямой
ВС
будет k![]() = =
= =
![]() .
ПрямаяАМ
перпендикулярна прямой ВС,
следовательно, используя (6.19), получаем
угловой коэффициент прямой АМ:
k
.
ПрямаяАМ
перпендикулярна прямой ВС,
следовательно, используя (6.19), получаем
угловой коэффициент прямой АМ:
k![]() =
=
![]() =
=
![]() .
Используем теперь формулу (6.8):
.
Используем теперь формулу (6.8):
y
– 1 =
![]() (x
– 2) или АМ:
4x
+ 3y
– 11 = 0.
(x
– 2) или АМ:
4x
+ 3y
– 11 = 0.
