
- •Вычисление определителей 2-го, 3-го и высших порядков
- •1. Определитель 2-го и 3-го порядков.
- •2. Определитель произвольного порядка.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Действия над матрицами, вычисление обратной матрицы. Решение матричных уравнений
- •1. Алгебра матриц.
- •2. Обратная матрица.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Решение систем линейных уравнений методом Крамера и Гаусса
- •1. Метод Крамера.
- •2. Метод Гаусса.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Векторная алгебра. Вычисление координат, модуля и направляющих косинусов вектора
- •1. Векторная алгебра.
- •2. Деление отрезка в данном отношении.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Скалярное, векторное и смешанное произведения векторов
- •1. Скалярное произведение векторов.
- •2. Векторное произведение векторов.
- •3. Смешанное произведение векторов.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Прямая линия на плоскости
- •1. Общее уравнение прямой.
- •2. Уравнение прямой в отрезках.
- •3. Каноническое уравнение прямой.
- •6. Параметрические уравнения прямой.
- •7. Прямая с угловым коэффициентом.
- •8. Нормальное уравнение прямой.
- •10. Условия параллельности и перпендикулярности прямых. Нахождение угла между прямыми.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Плоскость и прямая в пространстве
- •1. Общее уравнение плоскости.
- •2. Уравнение плоскости в отрезках.
- •3. Уравнение плоскости, проходящей через три точки, не лежащие на одной прямой.
- •5. Уравнение плоскости, параллельной двум неколлинеарным векторам и проходящей через точку.
- •7. Нормальное уравнение плоскости.
- •9. Общие уравнения прямой.
- •10. Канонические уравнения прямой.
- •12. Параметрические уравнения прямой.
- •13. Взаимное расположение прямых и плоскостей.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Кривые второго порядка
- •1. Эллипс.
- •2. Гипербола.
- •3. Парабола.
- •4. Единое определение кривой второго порядка.
- •5. Полярное уравнение кривой второго порядка.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Предел числовой последовательности. Предел функции
- •1. Предел числовой последовательности.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Раскрытие неопределенностей. Замечательные пределы
- •1. Замечательные пределы.
- •2. Сравнение бесконечно малых.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Непрерывность функции. Точки разрыва функции
- •1. Непрерывность функции.
- •2. Точки разрыва.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Вычисление производных
- •1. Производная и ее геометрический и механический смысл.
- •3. Производные основных элементарных функций.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Производная неявной, параметрически заданной и сложно-степенной функции
- •Задачи для самостоятельного решения
- •Производные высших порядков. Дифференциал функции. Приложения дифференциалов
- •1. Производные высших порядков.
- •2. Дифференциал функции.
- •3. Формула приближенного вычисления.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Правило Лопиталя. Точки экстремума функции.
- •1. Правило Лопиталя.
- •2. Возрастание и убывание функции.
- •3. Точки экстремума функции.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Исследование функций и построение графиков
- •1. Выпуклость и вогнутость функции.
- •2. Точки перегиба функции.
- •3. Асимптоты функции.
- •4. Общий план исследования функции и построение графика.
- •Примеры решения задач
- •Задачи для самостоятельного решения
12. Параметрические уравнения прямой.
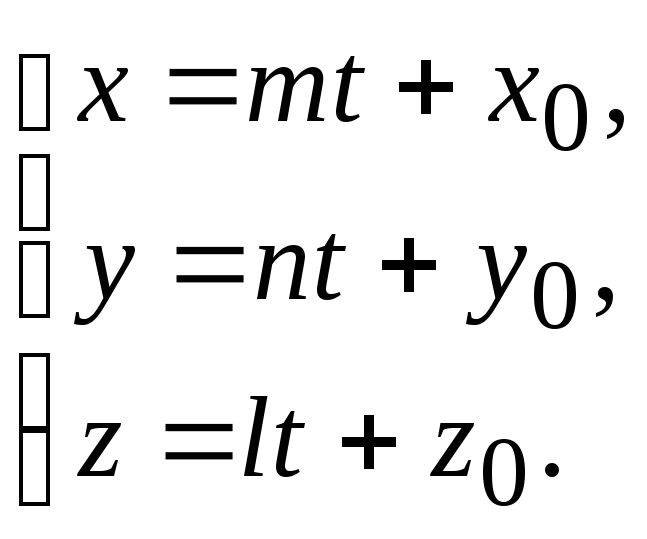 (7.12)
(7.12)
13. Взаимное расположение прямых и плоскостей.
1) Пусть в пространстве заданы плоскость и прямая L:
![]()
Условие параллельности прямой L и плоскости эквивалентно условию перпендикулярности нормали п(А, В, С) к плоскости и направляющего вектора а(l, m, n) прямой L и выражается равенством нулю скалярного произведения векторов п и а, т.е.
Al + Bm + Cn = 0 (7.13)
Условие перпендикулярности прямой L и плоскости эквивалентно условию коллинеарности векторов п и а, т.е.
![]() (7.14)
(7.14)
Как легко убедиться, условие принадлежности прямой L к плоскости выражается двумя равенствами:
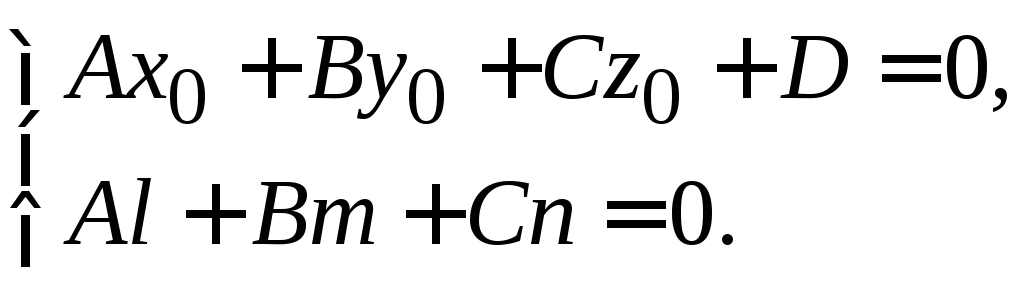 (7.15)
(7.15)
Угол между прямой L и плоскостью находится по формуле:
![]() (7.16)
(7.16)
2) Пусть в пространстве заданы две прямые своими каноническими уравнениями:

Условия
параллельности, перпендикулярности
![]() и
и![]() ,
а также угол между
,
а также угол между![]() и
и![]() определяются с использованием
направляющих векторов
определяются с использованием
направляющих векторов![]() и
и![]() данных прямых.
данных прямых.
Условие
параллельности
![]() (7.17)
(7.17)
Условие
перпендикулярности
![]() (7.18)
(7.18)
Угол
между прямыми
![]() (7.19)
(7.19)
3)
Пусть в пространстве заданы две плоскости
![]() и
и![]() своими общими уравнениями:
своими общими уравнениями:
![]()
Условия
параллельности, перпендикулярности
![]() и
и![]() ,
а также угол между
,
а также угол между![]() и
и![]() определяются аналогично, используя
векторы нормалейп
определяются аналогично, используя
векторы нормалейп![]() ип
ип![]() к плоскостям.
к плоскостям.
Условие
параллельности:
![]() (7.20)
(7.20)
Условие
перпендикулярности:
![]() (7.21)
(7.21)
Угол
между плоскостями:![]() (7.22)
(7.22)
Примеры решения задач
1.
Найти уравнение плоскости p,
проходящей через точку М(2;
2; –3) и параллельной плоскости
![]() :х
– 4у
– 2z
+ 1 = 0.
:х
– 4у
– 2z
+ 1 = 0.
Решение:
Поскольку плоскости параллельны, то
вектор нормали
![]() плоскостиp
плоскостиp![]() будет вектором нормали и для плоскости
p.
Применим формулу (7.6): p:
1(x
– 2) – 4(y
– 2) – 2(z
+ 3) = 0 или х
– 4у
– 2z
= 0.
будет вектором нормали и для плоскости
p.
Применим формулу (7.6): p:
1(x
– 2) – 4(y
– 2) – 2(z
+ 3) = 0 или х
– 4у
– 2z
= 0.
2. Найти уравнение плоскости p, проходящей через точку М0(–1; 2; 3) и через ось Oz.
Решение:
Так как p
проходит через Oz
и начало координат, то в общем уравнении
плоскости (7.1) C
= 0 и D
= 0. Тогда получаем
![]() .
Подставив туда точкуМ0(–1;
2; 3), найдем
.
Подставив туда точкуМ0(–1;
2; 3), найдем
![]() илиA
= 2B
и, следовательно, p:
2Bx
+ By
= 0 или 2x
+ y
= 0.
илиA
= 2B
и, следовательно, p:
2Bx
+ By
= 0 или 2x
+ y
= 0.
3.
Найти уравнение плоскости, проходящей
через три точки М![]() (0;
2; 3), М
(0;
2; 3), М![]() (–1;
0; 1), М
(–1;
0; 1), М![]() (2;
1; –1).
(2;
1; –1).
Решение: Используем формулу (7.3):
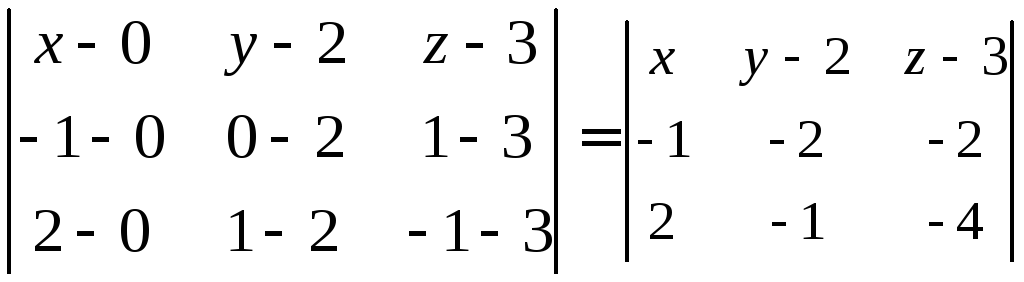 =
=
=
х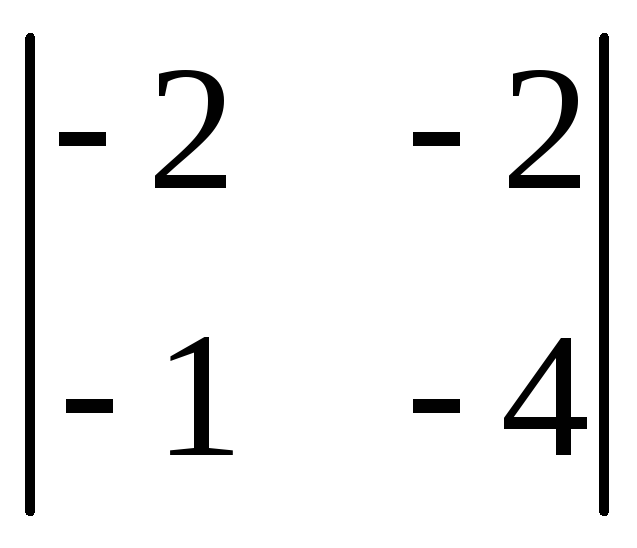 –
(у
– 2)
–
(у
– 2)![]() + (z
– 3)
+ (z
– 3)![]() = 6x
– 8y
+ 5z
+ 1
= 6x
– 8y
+ 5z
+ 1
Следовательно, получаем 6x – 8y + 5z + 1 = 0.
4.
При каких А
и С
плоскости p![]() :
Ax + 2y – z + 3 = 0
и p
:
Ax + 2y – z + 3 = 0
и p![]() :
2x
+ 6y
– Cz
+ 7 = 0 параллельны?
:
2x
+ 6y
– Cz
+ 7 = 0 параллельны?
Решение:
Воспользуемся условием параллельности
плоскостей (7.20):
![]() .
ПолучаемА
=
.
ПолучаемА
=
![]() =
=![]() ,С
= 3.
,С
= 3.
5. Найти
расстояние между параллельными
плоскостями
p![]() :
6х
+ 2у
+ 9z
= 0 и p
:
6х
+ 2у
+ 9z
= 0 и p![]() :
6x
+ 2y
+ 9z
– 11 = 0.
:
6x
+ 2y
+ 9z
– 11 = 0.
Решение:
На плоскости p![]() выберем точку М0.
Пусть x
= y
= 0, тогда z =
выберем точку М0.
Пусть x
= y
= 0, тогда z = ![]() ,
т.е.М0(0;
0;
,
т.е.М0(0;
0;![]() ).
Теперь расстояние между плоскостями
будет совпадать с расстоянием от точкиМ0
до
плоскости
p
).
Теперь расстояние между плоскостями
будет совпадать с расстоянием от точкиМ0
до
плоскости
p![]() .
Для нахождения этого расстояния
используем формулу (7.8):
.
Для нахождения этого расстояния
используем формулу (7.8):
d
=
 .
.
6.
Составить канонические уравнения прямой
по данным общим уравнениям

Решение: Найдем направляющий вектор этой прямой:
![]() =
=
![]() =
=
 = –i
–
j
+ 2k
= (–1; –1; 2).
= –i
–
j
+ 2k
= (–1; –1; 2).
Далее
найдем точку, лежащую на прямой. Пусть
в системе уравнений z
= 0, тогда система упростится:
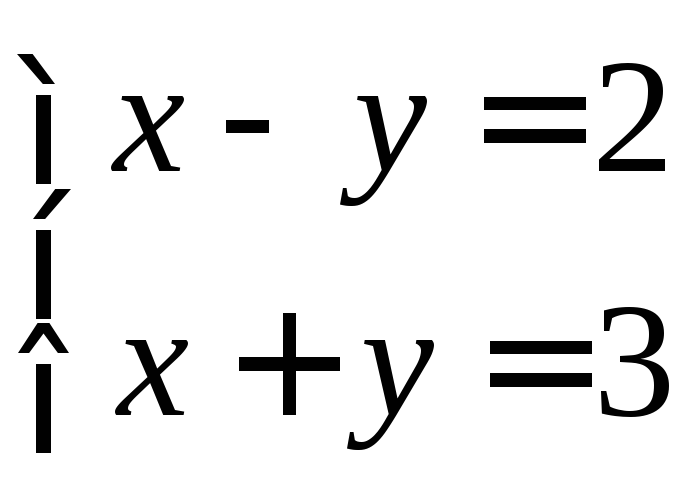 и даст решение:х
= 2,5; у
= 0,5. В результате имеем точку на прямой
M0(2,5;
0,5; 0) и канонические уравнения прямой
(7.10) примут вид
и даст решение:х
= 2,5; у
= 0,5. В результате имеем точку на прямой
M0(2,5;
0,5; 0) и канонические уравнения прямой
(7.10) примут вид
![]() .
.
7.
При каком m
прямые l![]() :
:
![]() иl
иl![]() :
:
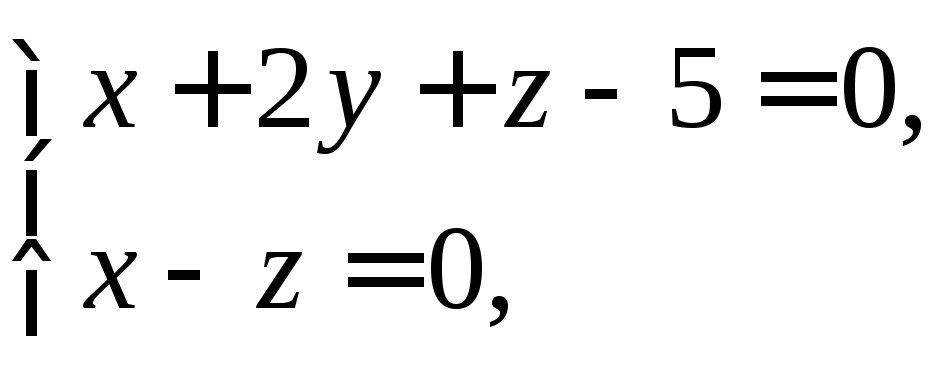 перпендикулярны?
перпендикулярны?
Решение:
Направляющий вектор прямой
![]() есть
есть![]() .
Найдем направляющий вектор прямой
.
Найдем направляющий вектор прямой![]() :
:![]() =
=![]() =
=
 = –2i
+
2j
– 2k.
Т.е.
= –2i
+
2j
– 2k.
Т.е.
![]() .
Далее используем условие перпендикулярности
(7.18) прямых:m·(–2)
+2·2 + 3·(–2) = 0. Отсюда получаем m
= –1.
.
Далее используем условие перпендикулярности
(7.18) прямых:m·(–2)
+2·2 + 3·(–2) = 0. Отсюда получаем m
= –1.
8. Найти параметрические уравнения прямой l, проходящей через точку М0(–1; 2; 3) и перпендикулярной к плоскости p: 3x + y – 5z + 1 = 0.
Решение:
Поскольку l
![]() p,
то вектор нормали
p,
то вектор нормали
![]() к плоскостир
является направляющим вектором прямой
l.
Т.е.
к плоскостир
является направляющим вектором прямой
l.
Т.е.
![]() .
Тогда параметрические уравнения (7.12)
примут вид
.
Тогда параметрические уравнения (7.12)
примут вид
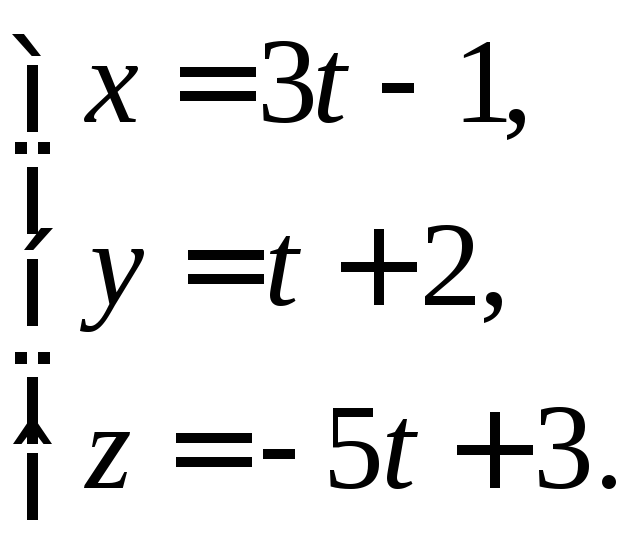
9.
Найти точку пересечения плоскости x
– 2y
+ 3z
+ 5 = 0 и прямой
![]() .
.
Решение: Запишем уравнения прямой в параметрическом виде (7.12):
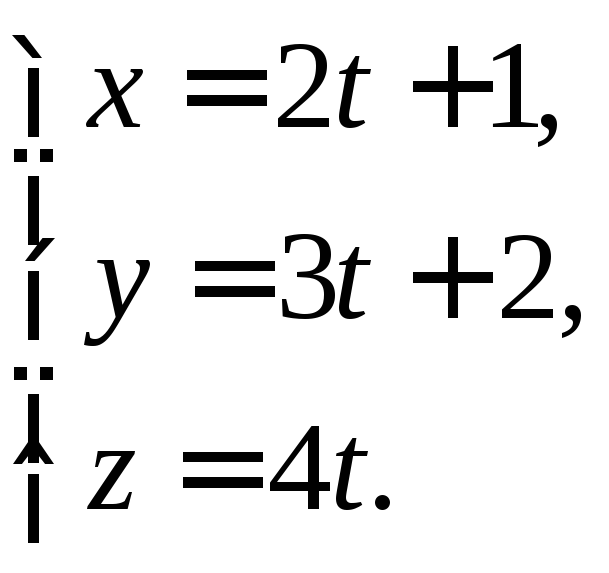
Подставим
полученные равенства в уравнение
плоскости (2t
+ 1) – 2(3t
+ 2) + 3(4t)
+ 5 = 0. Решив полученное уравнение, найдем
t
=
![]() .
Заменив в параметрических уравнениях
параметрt
на
.
Заменив в параметрических уравнениях
параметрt
на
![]() ,
найдем координаты точки пересечения
прямой и плоскости (
,
найдем координаты точки пересечения
прямой и плоскости (![]() ,
,![]() ,
–1).
,
–1).
10.
Найти угол между прямой l:
 и плоскостьюp:
2x
+ y
– z
+ 1 = 0.
и плоскостьюp:
2x
+ y
– z
+ 1 = 0.
Решение: Найдем направляющий вектор прямой l:
![]() =
=
![]() =
=
 = 2i
–
j
+
k.
= 2i
–
j
+
k.
Теперь найдем угол между l и p по формуле (7.16):
sin![]() =
=
 =
=![]() .
.
