Примеры решения задач

1. Расстояние между фокусами равно 8, а малая полуось равна 3. Написать уравнение эллипса.

Решение: Так как 2с = 8 и b = 3, то c = 4, a = = 5, и уравнение эллипса имеет вид:.

2. Даны: вещественная полуось a = 2и эксцентриситет=. Написать уравнение гиперболы.

Решение: Так как с = a, тоb = = a = 2 и уравнение гиперболы имеет вид .

3. Привести уравнение 2x + 3y – 4x + 6y – 7 = 0 к каноническому виду, определить тип кривой.

Решение: Выполним приведение к полным квадратам:

2(x – 1) + 3(y + 1) – 12 = 0.

Приводим уравнение к каноническому виду:

.

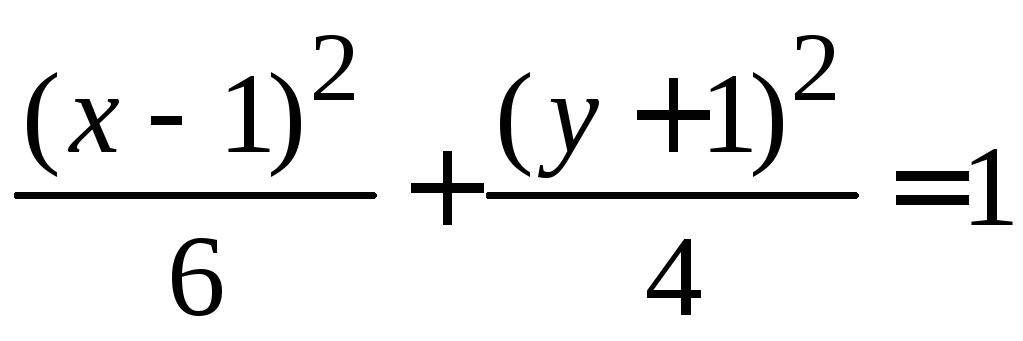Очевидно, это уравнение является уравнением эллипса. Координаты центра кривой (1; –1). Полуоси эллипса .

4. Привести уравнение кривой второго порядка к каноническому виду и построить ее: .

Решение: Выделим полные квадраты с переменными х и у:

.

Перепишем это уравнение в каноническом виде:

.

Полученное уравнение является уравнением смещенной гиперболы, центр которой находится в точке с координатами (1, –2). Полуоси гиперболы а = 5 и b = 3. Для построения гиперболы сначала необходимо отметить центр гиперболы, затем начертить прямоугольник со сторонами 10 и 6, центр которого совпадает с центром гиперболы (см. рис. 8.7). Далее надо провести диагонали в полученном прямоугольнике, которые будут являться асимптотами гиперболы, после этого можно построить ветви гиперболы (см. рис. 8.8).

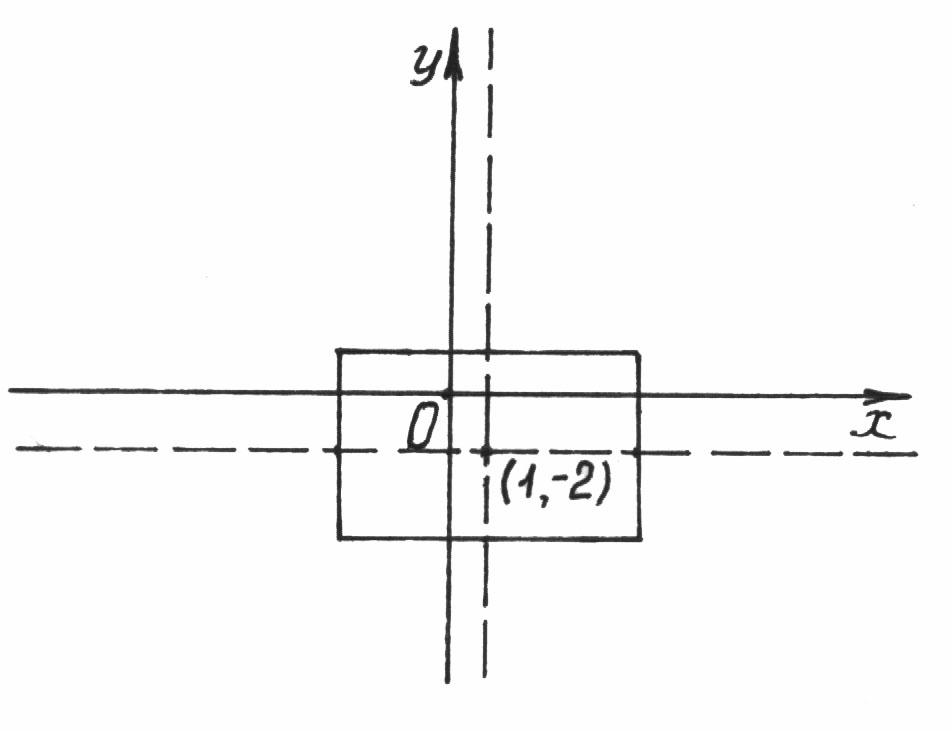
Рис. 8.7 Рис. 8.8

5. Привести уравнение x + 6х + y + 10 = 0 к каноническому виду, определить ее тип и построить кривую.

Решение: Выполним приведение к полному квадрату:

(x + 3) = – (y + 1).

Очевидно, это есть уравнение параболы. Координаты вершины параболы (–3; –1), ветви ее направлены вниз. Фокальный параметр р =. Парабола построена на рис. 8.9.

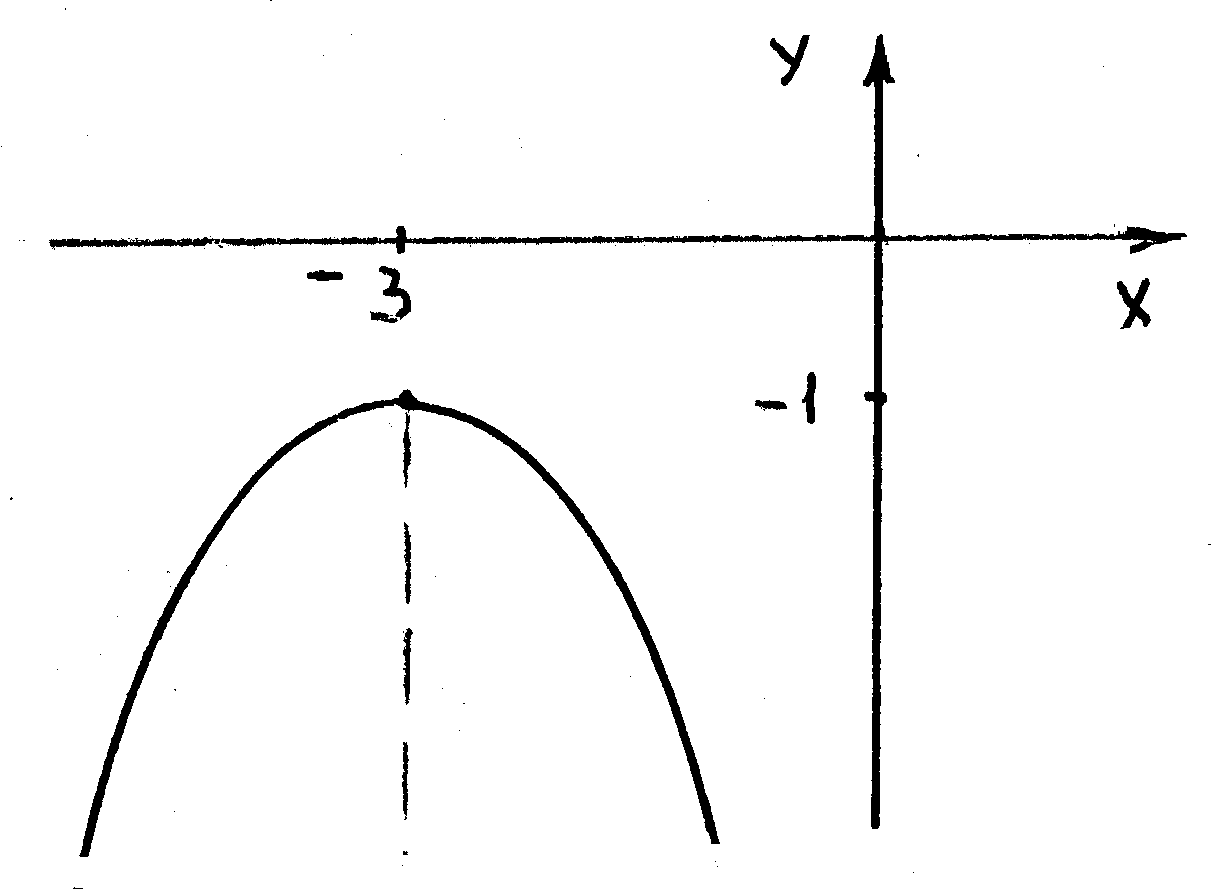
Рис. 8.9

6. Привести уравнение x + y = 4x к каноническому виду. Записать для него полярное уравнение.

Решение: Выполним приведение к полному квадрату: (x – 2) + y = 4. Это уравнение окружности с центром в точке (2; 0), радиуса R = 2. Переходя к полярному уравнению, получим:

rcos + rsin = 4rcos или r = 4cos.

Задачи для самостоятельного решения

1. Привести к каноническому виду следующие уравнения и построить соответствующие кривые:

а) 4x + 9y – 16x – 18y – 11 = 0; б) x+ 2х – y = 0;

в) x – 9y + 6x + 18y – 9 =0; г) 9x + y – 18x + 2y+1 = 0.

2. Построить графики следующих функции в полярной системе координат по точкам. Значение угла менять от 0 с интервалом, указанным в квадратных скобках. Найти уравнения в прямоугольной системе координат.

а) , []; б) , [];

в) , []; г) , [].

3. Написать уравнение касательной к окружности (х + 1) + (у – 3) = 25 в точке (3; 6).

4. Привести к каноническому виду следующие уравнения и построить соответствующие кривые:

а) 36x + 36y– 36х – 24y – 23 = 0; б) x – y – х + y – 1 = 0;

в) x+ 4y– 4x – 8y + 8 = 0; г) x + 4y + 8y + 5 = 0;

д) x – 6ху + y = 8; е) x + ху + y = 1.

5. Известно, что прямая 2х – 5у – 30 = 0 касается эллипса . Найти точку их прикосновения.

6. Дана гипербола . Написать уравнения асимптот.

7. Дана парабола у = – 8х. Через точку (–1; 1) провести такую хорду, которая в этой точке делилась бы пополам.

8. Построить графики следующих функций в полярной системе координат по точкам. Значение угла менять от 0 с интервалом, указанным в квадратных скобках. Найти уравнения в прямоугольной системе координат.

а) , []; б) , [];

в) , []; г) , [].

Ответы:

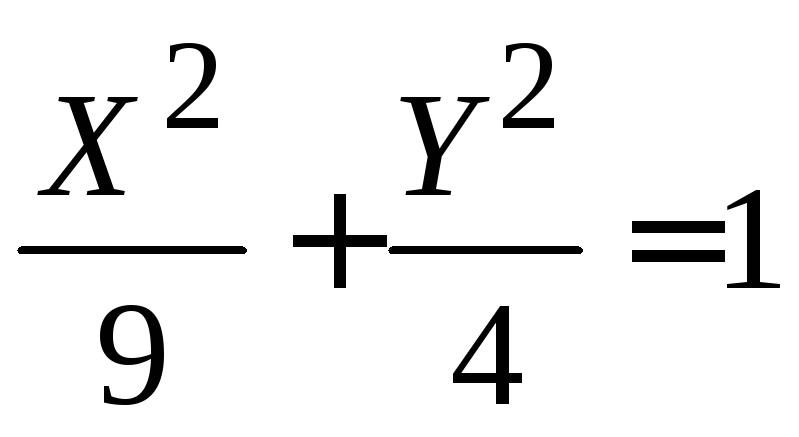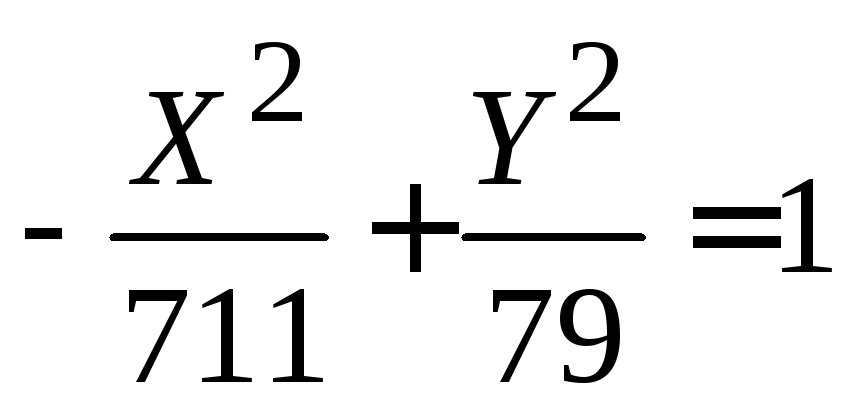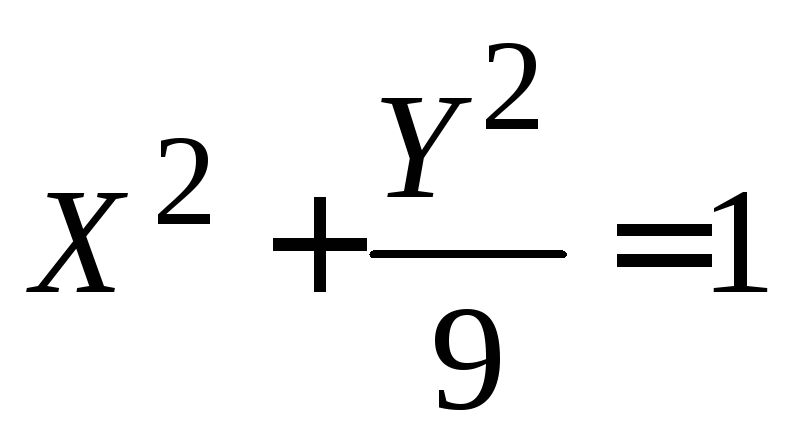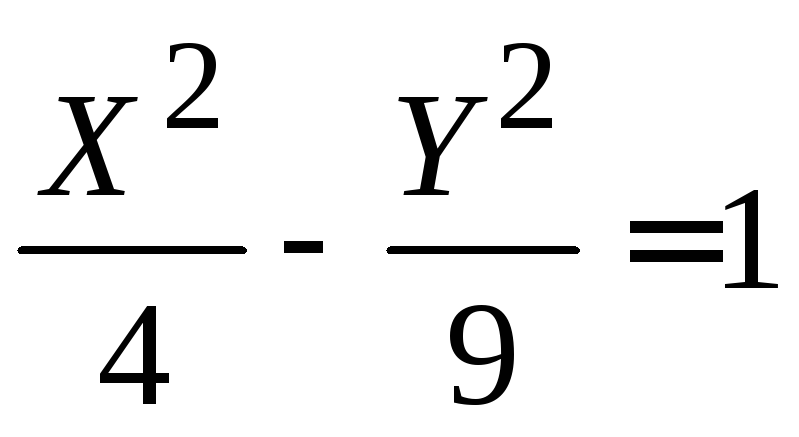1) а) Эллипс , новое начало в точке (2; 1); б) парабола, новое начало в точке (–1; –1); в) гипербола, новое начало в точке (–3; 9); г) эллипс, новое начало в точке (1; –1);3) 4х + 3у – 30 = 0; 4) а) Окружность ; б) гипербола, новое начало в точке (2; 3); в) точка (2; 1); г) мнимый эллипс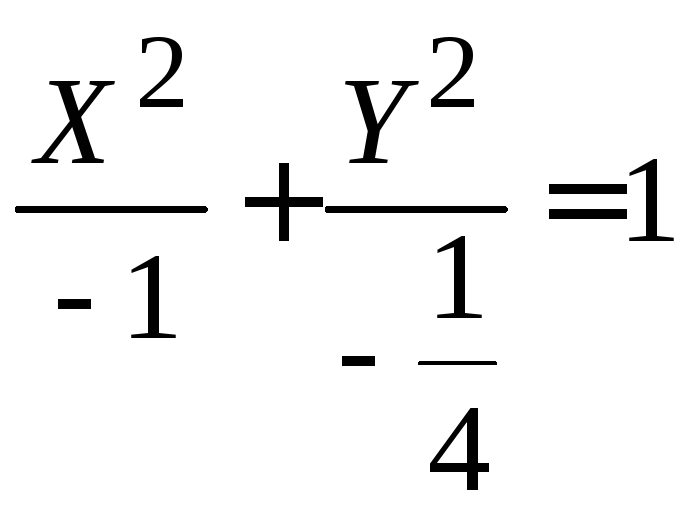,Х = х, Y = у + 1; д) гипербола 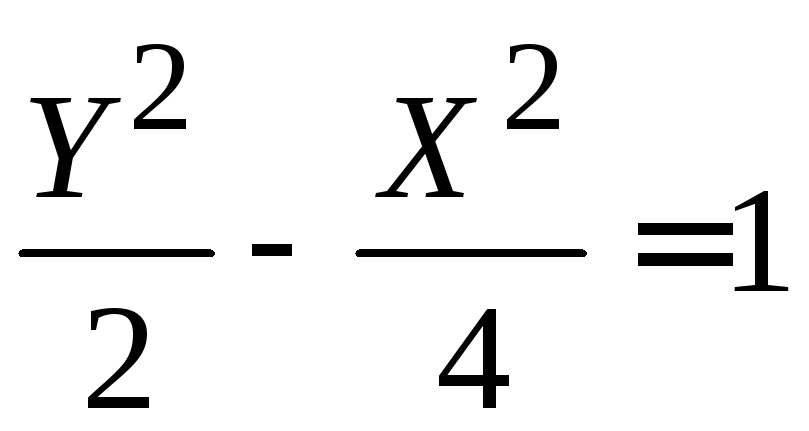, φ = 135º; е) эллипс, φ = 135º;5) (5; –4); 6) у = х; 7) 4х + у +3 = 0.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 9