
- •Вычисление определителей 2-го, 3-го и высших порядков
- •1. Определитель 2-го и 3-го порядков.
- •2. Определитель произвольного порядка.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Действия над матрицами, вычисление обратной матрицы. Решение матричных уравнений
- •1. Алгебра матриц.
- •2. Обратная матрица.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Решение систем линейных уравнений методом Крамера и Гаусса
- •1. Метод Крамера.
- •2. Метод Гаусса.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Векторная алгебра. Вычисление координат, модуля и направляющих косинусов вектора
- •1. Векторная алгебра.
- •2. Деление отрезка в данном отношении.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Скалярное, векторное и смешанное произведения векторов
- •1. Скалярное произведение векторов.
- •2. Векторное произведение векторов.
- •3. Смешанное произведение векторов.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Прямая линия на плоскости
- •1. Общее уравнение прямой.
- •2. Уравнение прямой в отрезках.
- •3. Каноническое уравнение прямой.
- •6. Параметрические уравнения прямой.
- •7. Прямая с угловым коэффициентом.
- •8. Нормальное уравнение прямой.
- •10. Условия параллельности и перпендикулярности прямых. Нахождение угла между прямыми.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Плоскость и прямая в пространстве
- •1. Общее уравнение плоскости.
- •2. Уравнение плоскости в отрезках.
- •3. Уравнение плоскости, проходящей через три точки, не лежащие на одной прямой.
- •5. Уравнение плоскости, параллельной двум неколлинеарным векторам и проходящей через точку.
- •7. Нормальное уравнение плоскости.
- •9. Общие уравнения прямой.
- •10. Канонические уравнения прямой.
- •12. Параметрические уравнения прямой.
- •13. Взаимное расположение прямых и плоскостей.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Кривые второго порядка
- •1. Эллипс.
- •2. Гипербола.
- •3. Парабола.
- •4. Единое определение кривой второго порядка.
- •5. Полярное уравнение кривой второго порядка.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Предел числовой последовательности. Предел функции
- •1. Предел числовой последовательности.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Раскрытие неопределенностей. Замечательные пределы
- •1. Замечательные пределы.
- •2. Сравнение бесконечно малых.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Непрерывность функции. Точки разрыва функции
- •1. Непрерывность функции.
- •2. Точки разрыва.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Вычисление производных
- •1. Производная и ее геометрический и механический смысл.
- •3. Производные основных элементарных функций.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Производная неявной, параметрически заданной и сложно-степенной функции
- •Задачи для самостоятельного решения
- •Производные высших порядков. Дифференциал функции. Приложения дифференциалов
- •1. Производные высших порядков.
- •2. Дифференциал функции.
- •3. Формула приближенного вычисления.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Правило Лопиталя. Точки экстремума функции.
- •1. Правило Лопиталя.
- •2. Возрастание и убывание функции.
- •3. Точки экстремума функции.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Исследование функций и построение графиков
- •1. Выпуклость и вогнутость функции.
- •2. Точки перегиба функции.
- •3. Асимптоты функции.
- •4. Общий план исследования функции и построение графика.
- •Примеры решения задач
- •Задачи для самостоятельного решения
Примеры решения задач
1.
Найти линейную комбинацию матриц
![]() ,
где
,
где![]() ,
,![]() .
.
Решение:
![]()
![]() .
.
2.
Пусть
![]() – матрица размерности 2x
3,
– матрица размерности 2x
3,
 – матрица размерности 3 х 3. Найти
произведения
– матрица размерности 3 х 3. Найти
произведения![]() и
и![]() (если это возможно).
(если это возможно).
Решение: Используем формулу (2.1):
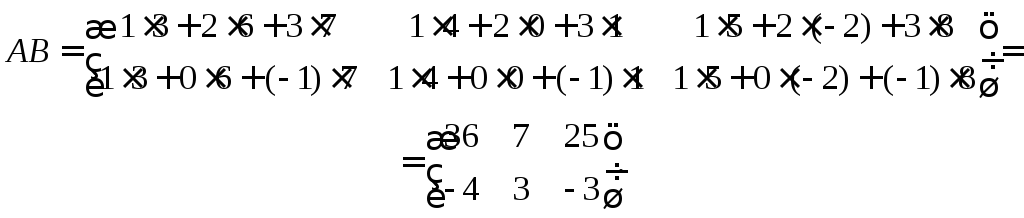
Произведение
![]() не существует, так как число столбцов
матрицыB
не совпадает с числом строк матрицы A:
не существует, так как число столбцов
матрицыB
не совпадает с числом строк матрицы A:
![]() .
.
3.
Найти![]() ,
если
,
если![]() .
.
Решение:
![]() .
.
![]() .
.
4.
Найти значение матричного многочлена
![]() ,
если
,
если
![]() ,
,
![]() .
.
Решение:
![]() .
.
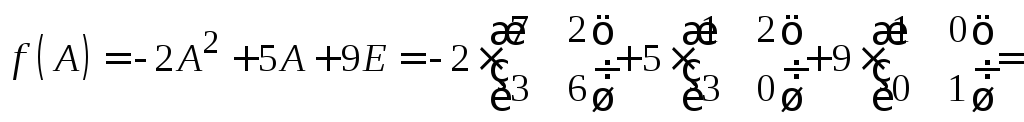
![]() .
.
5.
Транспонировать матрицу
![]() .
.
Решение:
Так как у матрицы A
две строки и три столбца, то у матрицы
![]() будет три строки и два столбца:
будет три строки и два столбца: .
.
6.
Дана матрица
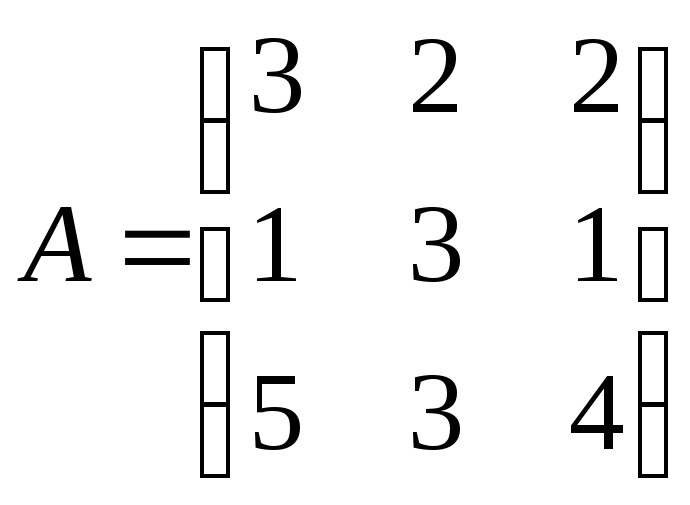 .
Найти обратную матрицу.
.
Найти обратную матрицу.
Решение: Воспользуемся первым способом нахождения обратной матрицы, т.е. формулой (2.2). Вычисляем определитель матрицы A:
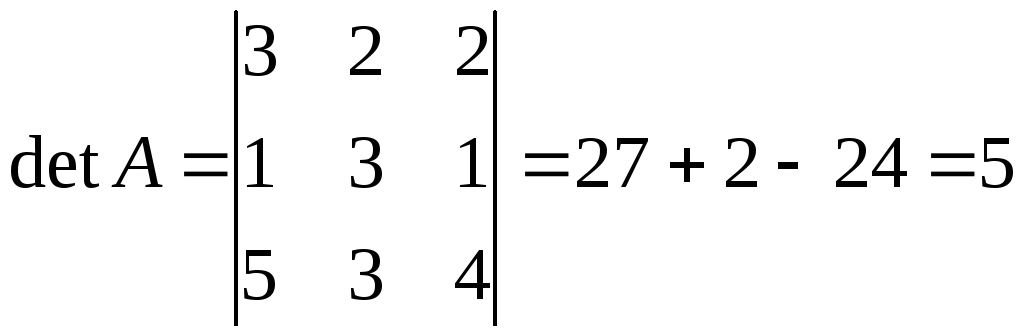 .
.
Так
как
![]() ,
то матрица
,
то матрица![]() существует. Найдем алгебраические
дополнения ко всем элементам матрицыA:
существует. Найдем алгебраические
дополнения ко всем элементам матрицыA:
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Составим
присоединенную матрицу:
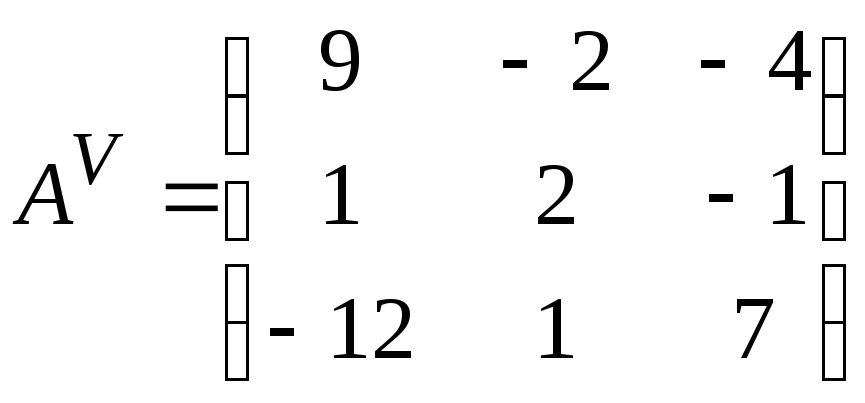 .
Находим обратную матрицу, поделив каждый
элемент присоединенной матрицы на
определитель матрицы A.
Получаем ответ:
.
Находим обратную матрицу, поделив каждый
элемент присоединенной матрицы на
определитель матрицы A.
Получаем ответ:
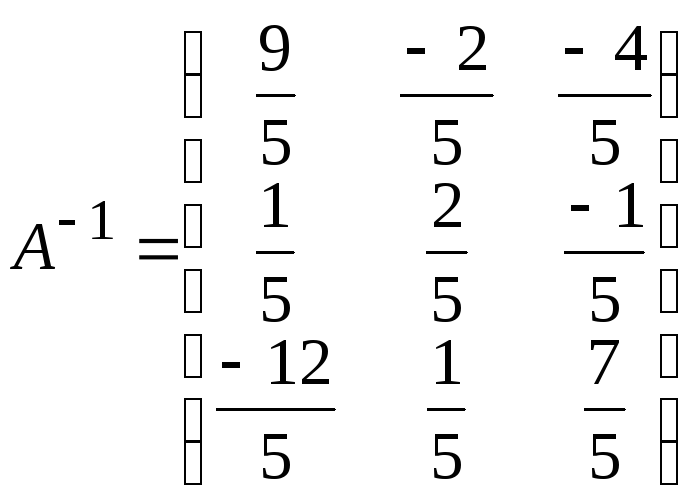 .
.
7.
Решить матричное уравнение:
![]() .
.
Решение:
Запишем данное матричное уравнение в
виде
![]() .
Его решением является матрица
.
Его решением является матрица
![]() (если существует матрица
(если существует матрица![]() ).
Найдем определитель матрицыA:
).
Найдем определитель матрицыA:
![]() .
Значит,
обратная матрица
существует, и исходное уравнение имеет
(единственное) решение. Найдем обратную
матрицу:
.
Значит,
обратная матрица
существует, и исходное уравнение имеет
(единственное) решение. Найдем обратную
матрицу:
![]() ,
,
![]() ;
;
![]() ,
,
![]() .
Найдем
решение матричного уравнения:
.
Найдем
решение матричного уравнения:
![]() .
.
8.
Найти обратную к матрице
![]() ,
используя метод элементарных
преобразований.
,
используя метод элементарных
преобразований.
Решение: Припишем справа единичную матрицу
![]() .
.
Разделив первую строку на три и обнулив элемент в первом столбце ниже тройки, получим
 .
.
Умножив
вторую строку на три и обнулив элемент
во втором столбце выше
![]() ,
получим
,
получим
![]() .
.
Таким
образом,
![]() .
.
Задачи для самостоятельного решения
1.
Найти линейную комбинацию матриц
![]() ,
где
,
где
 .
.
2.
Найти произведения матриц
![]() и
и![]() (если они существуют), где
(если они существуют), где
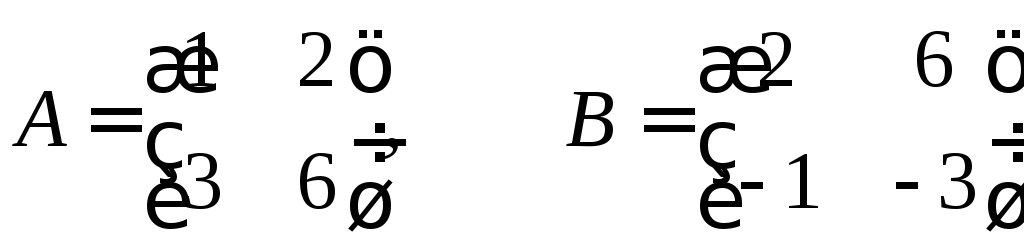 .
.
3. Проверить коммутируют ли матрицы
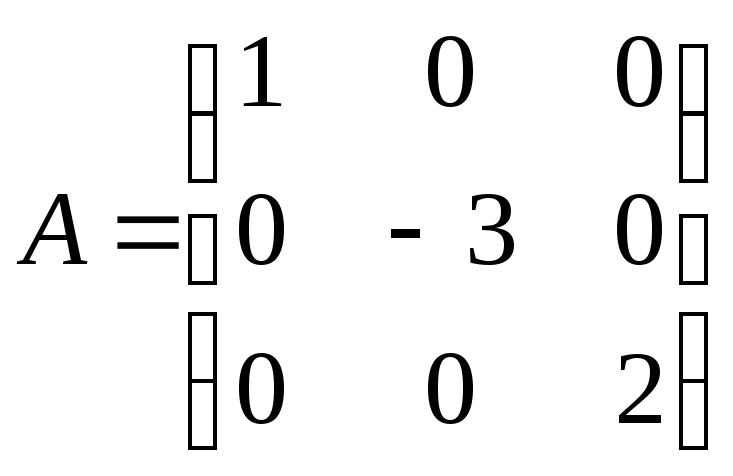 и
и
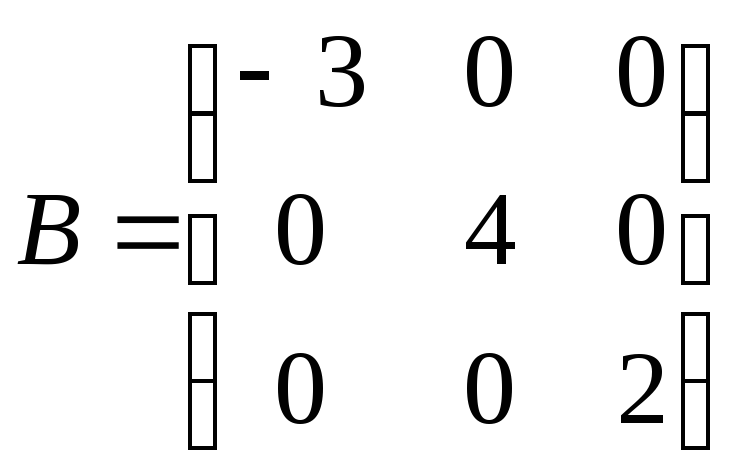 .
.
4.
Найти значение матричного многочлена
![]() ,
если
,
если![]() и
и![]() .
.
5.
Вычислить произведение
![]() при заданной матрице
при заданной матрице
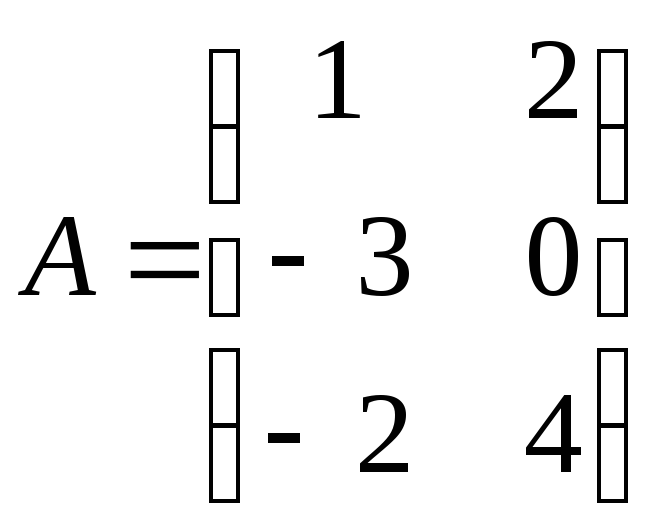 .
.
6.
Привести к ступенчатому виду матрицу
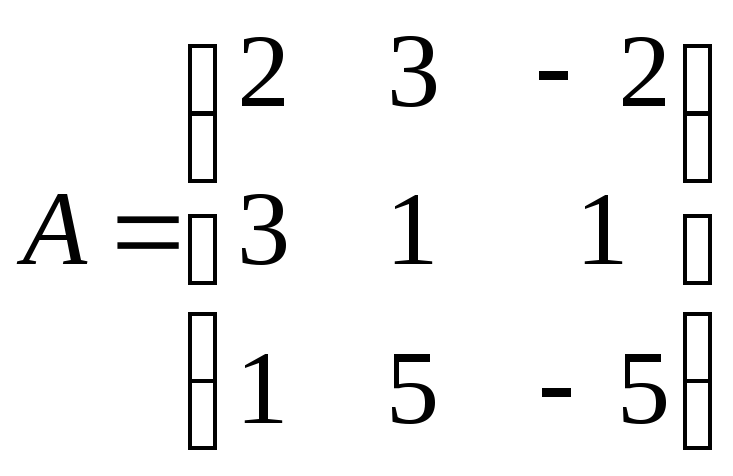 .
.
7.
Найти произведения матриц
![]() и
и![]() ,
где
,
где
![]() .
.
8.
Найти обратную матрицу к матрице
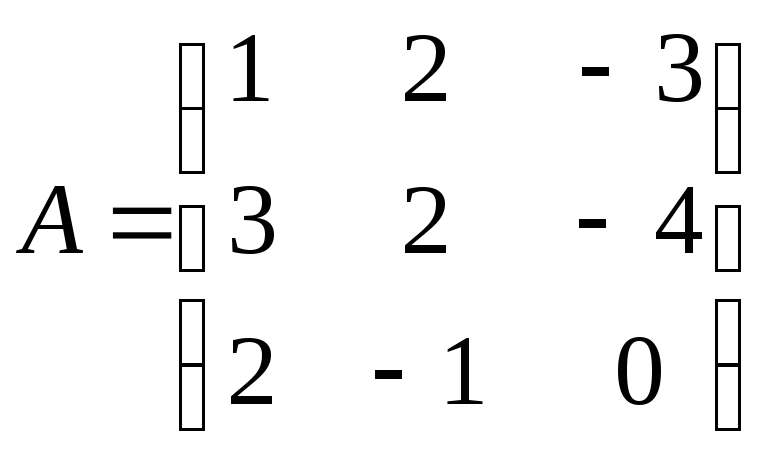 .
.
Решить матричные уравнения:
9.
![]() ;
;
10.
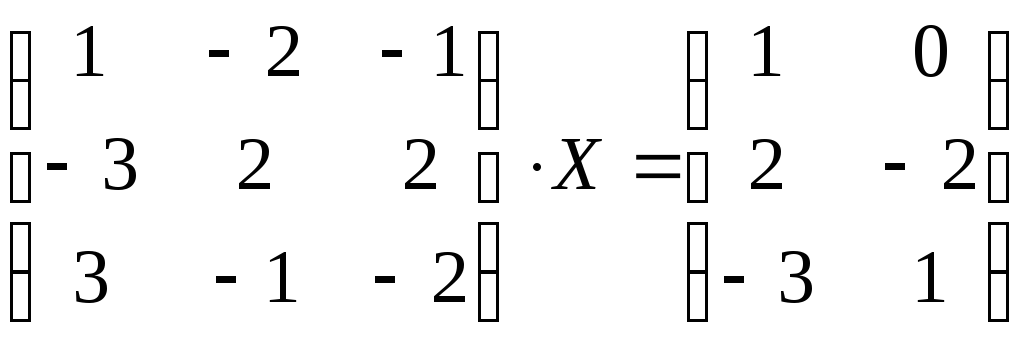 .
.
11.
Найти линейную комбинацию матриц
![]() ,
где
,
где
 .
.
12.
Найти произведения матриц
![]() и
и![]() (если они существуют), где
(если они существуют), где
 .
.
13.
Проверить, коммутируют ли матрицы
 и
и
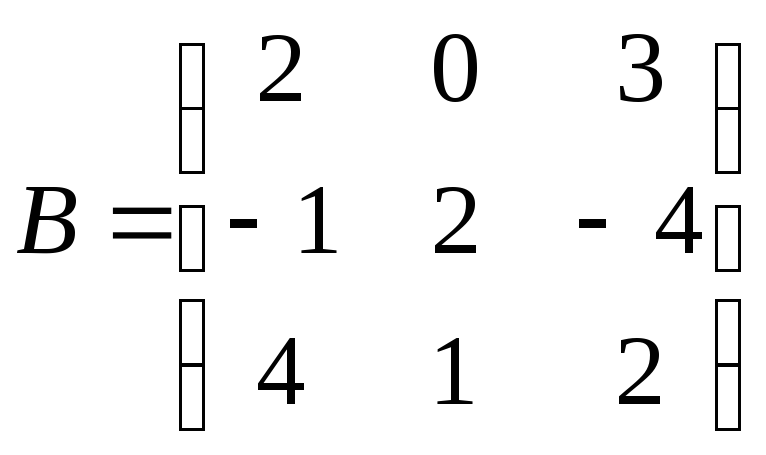 .
.
14.
Найти значение матричного многочлена
![]() ,
если
,
если
![]() .
.
15.
Вычислить произведение
![]() при заданной матрице
при заданной матрице![]() .
.
16.
Привести к ступенчатому виду матрицу
 .
.
17.
Найти произведения матриц
![]() и
и![]() ,
если
,
если
![]() .
.
18.
Найти обратную матрицу к матрице
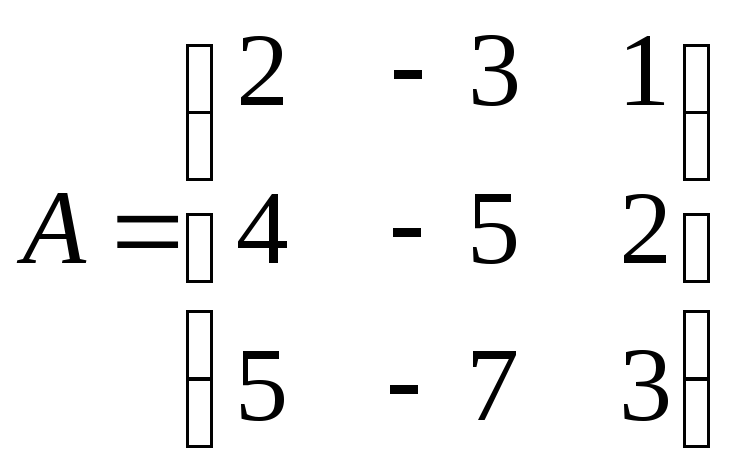 .
.
Решить матричные уравнения:
19.
![]() ;
;
20.
 .
.
Ответы:
1)
 ;
2)
;
2)
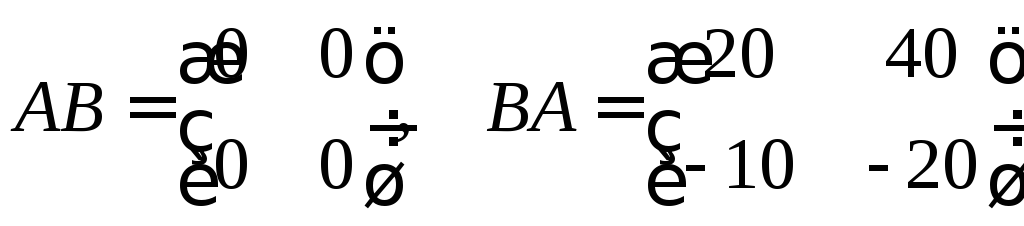 ;3)
Да;
4)
;3)
Да;
4) ![]() ;5)
;5)
 ;
6)
;
6)
 ;7)
;7)
![]() ;8)
;8) 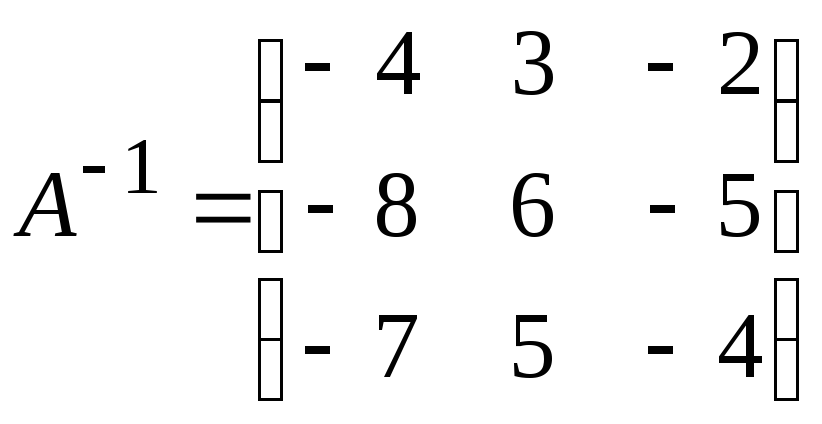 ;9)
;9)
![]() ;10)
;10)
 ;11)
;11)
 ;
12)
;
12)
![]() ;13)
Нет; 14)
;13)
Нет; 14)
![]() ;15)
;15) ![]() ;
16)
;
16)  ;17)
;17)
![]() ;18)
;18)
 ;19)
;19) ![]() ;20)
;20)  .
.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 3
Решение систем линейных уравнений методом Крамера и Гаусса
1. Метод Крамера.
Система уравнений вида
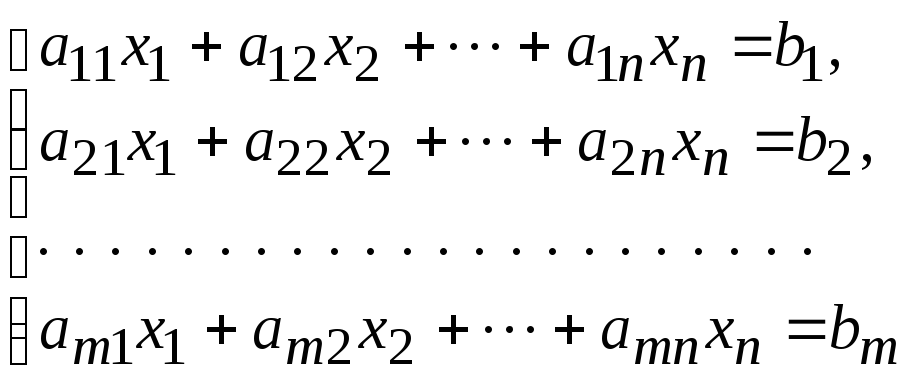 (3.1)
(3.1)
называется системой m линейных уравнений с n неизвестными.
Коэффициенты этих уравнений записываются в виде матрицы А, называемой матрицей системы, а числа, стоящие в правой части системы, образуют столбец В, называемый столбцом свободных членов. Неизвестные системы так же записываются в столбец, называемый столбец неизвестных:
 ,
,
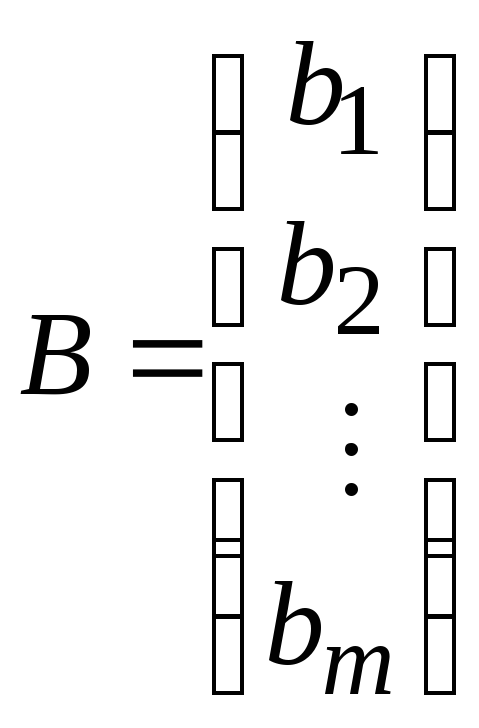 ,
,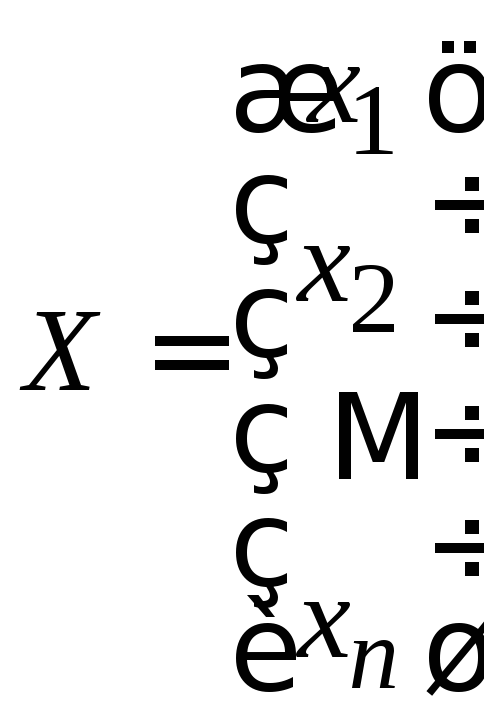
Используя
произведение матриц, можно записать
данную систему в матричном виде:
![]() .
.
Совокупность
чисел
![]() называетсярешением
системы,
если каждое уравнение системы обращается
в равенство после подстановки в него
чисел
называетсярешением
системы,
если каждое уравнение системы обращается
в равенство после подстановки в него
чисел
![]() вместо неизвестных
вместо неизвестных![]() .
.
Системы, не имеющие решения, называются несовместными.
Системы, имеющие решения, называются совместными. Заметим, что система может иметь единственное решение, а может иметь бесконечно много решений.
Для нахождения единственного решения систем с одинаковым количеством уравнений и неизвестных есть метод, называемый метод Крамера.
Система n уравнений с n неизвестными
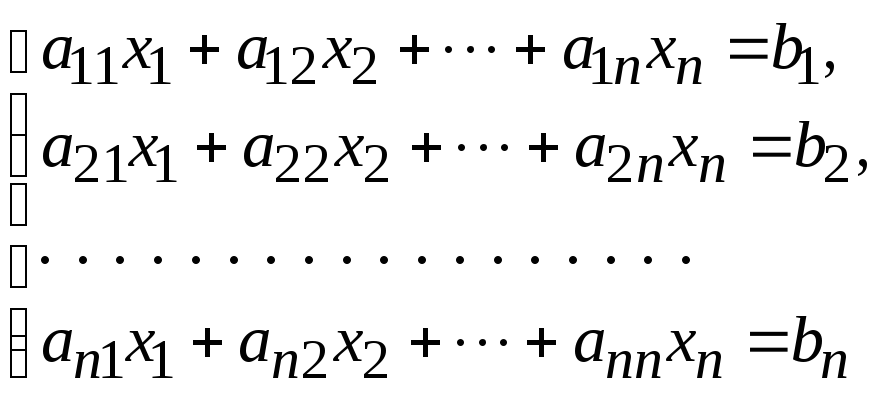
имеет единственное решение, если определитель матрицы системы отличен от нуля. Это решение находится по формулам Крамера:
![]() ,
(3.2)
,
(3.2)
где – определитель матрицы системы, а k – определитель матрицы, полученной из матрицы системы заменой k-го столбца столбцом свободных членов.
