7.6. Эффект Зеебека

Эффект Зеебека относится к термоэлектрическимявлениям. К этой группе относятся также эффекты Пельтье и Томсона.

В 1823 г. Т. Зеебек установил, что в цепи, состоящей из разнородных проводящих материалов, возникает термоэлектрический ток, если контакты материалов имеют различную температуру. Если цепь разорвать в произвольном месте, то на концах разомкнутой цепи появляется разность потенциалов, называемая термоэлектродвижущей силой (термоЭДС). Зеебек доказал, что разность потенциалов в разомкнутой цепи dU зависит от разности температур и вида материала.

, (7.58)

или

, (7.59)

где - термоэлектрический коэффициент Зеебека.

dU(α) принято считать положительной величиной, если потенциал горячего контакта выше, чем потенциал холодного.

Рассмотрим эффект на примере цепи, состоящей из двух разнородных материалов 1 и 2 (рис. 7.11).

а)

б)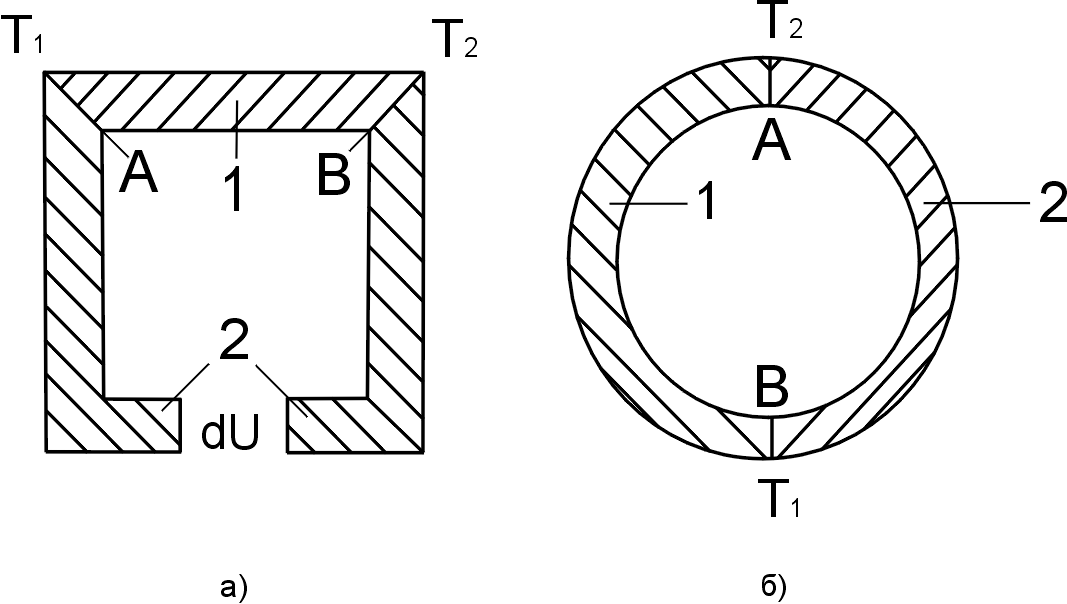

Рис. 7.11. Эффект Зеебека: а– термоЭДС;б– термоток,Т₂>T₁

Существует три источника термоЭДС: образование направленного потока носителей в проводнике при наличии градиента температур (объемнаясоставляющая–U_об), изменение положения уровня Ферми в контакте при изменении температуры контакта (контактнаясоставляющая–U_к) и увлечение электронов фононами.

Рассмотрим физическую природу каждого механизма.

Объемная составляющая термоЭДС.Представим, что на концах однородного проводника 1 возникает разность температурТ₂-Т₁, так что вдоль проводника отBк А существует градиент температуры (см. рис. 7.11). Носители тока, находящиеся в более нагретых областях, обладают большей скоростью и энергией, чем те, которые находятся в менее нагретых областях проводника. Поэтому в проводнике от горячего конца к холодному начинается перемещение зарядов. Если носителями заряда являются электроны, то холодный конец вследствие их избытка заряжается отрицательно, а горячий – положительно.

Приблизительную оценку этой составляющей термоЭДС можно привести следующим образом.

Электронный газ создает в проводнике давление Р, пропорциональное концентрации электроновn

, (7.60)

где Ē –средняя энергия электронов.

Наличие градиента температуры вызывает перепад этого давления, для уравновешивания которого формируется поле с напряженностью Е_об.

Из условия равновесия этих процессов можно вывести выражения для коэффициента объемной термоЭДС

. (7.61)

Эту составляющую термоЭДС называют теромодиффузионной.

Как правило, в электронном проводнике α_обнаправлена от горячего конца к холодному, но для ряда переходных металлов и сплавов имеются исключения [14].

Контактная составляющая термоЭДС.Как известно, в любой области системы, находящейся в состоянии термодинамического равновесия, химический потенциал (уровень Ферми) одинаков. Выше мы рассматривали различные контакты и установили, что это обстоятельствоприводит к формированию разности потенциалов U_к на контакте. В цепи (см. рис. 7.11), разности потенциалов на контактах А и В имеют равные значения и противоположные полярности в случае равенства температур контактов. При изменении температуры контакта там изменяется положение уровня Ферми. Так, в электронных полупроводниках при повышении температуры уровень Ферми смещается вниз и на холодном контакте он будет располагаться выше, чем на горячем. Это приведет к возникновению разности потенциалов.

, (7.62)

где U_кх (U_кг) – контактная разность потенциалов на холодном (горячем) контакте.

Можно записать выражения в дифференциальной форме для контактной составляющей термоЭДС

. (7.63)

Из выражения (7.63) следует, что

. (7.64)

Суммируя контактную и объемную дифференциальную термоЭДС, получим

. (7.65)

В металлах и полупроводниках выражение (7.65) приводит к различным результатам.

ТермоЭДС в металлах. Подставляя среднюю энергию электроновĒи энергию Фермив выражение (7.65), получим формулу для дифференциальной термоЭДС в металлах

, (7.66)

Более строгий расчет приводит к несколько иной форме

, (7.67)

где r– показатель степени в зависимости.

Из последнего выражения следует, что дифференциальный коэффициент термоЭДС растет с температурой. Поскольку kТ<<E_ф, величина термоЭДС в металлах мала. Например, для серебраα_μ≈ 8∙10^-6В/К.

ТермоЭДС в полупроводниках.Ее объемная составляющая много больше, чем в металлах, поскольку там существует сильная зависимость концентрации носителей от температуры. Поэтому кроме процессов, характерных для металлов, в полупроводниках возникает диффузионный ток носителей из горячей области в холодную. На концах однородного полупроводника возникает объемная термоЭДС, которая в свою очередь формирует дрейфовый ток. В условиях термодинамического равновесия дрейфовый и диффузионный токи равны, т. е. для электронного полупроводника можно записать выражение

. (7.68)

Решение этого уравнения приводит к следующему выражению для диффузионной объемной составляющей термоЭДС.

, (7.69)

Найдем объемную термодиффузионную составляющую термоЭДС в полупроводниках. Давление электронного газа в невырожденном полупроводнике составляет

, (7.70)

Подставив (7.70) в (7.61), получим

. (7.71)

Более точный результат дает выражение

, (7.72)

где r– показатель степени в зависимости.

Выражение для уровня Ферми в невырожденном электронном полупроводнике можно записать в виде

. (7.73)

Подставляя (7.73) в (7.64), получим выражение для контактной составляющейтермоЭДС в полупроводниках

. (7.74)

Суммируя диффузионную (7.69), термодиффузионную (7.72) объемную составляющую и контактную составляющего термоЭДС (7.74), получим выражение для полной дифференциальной термоЭДС в электронном полупроводнике

, (7.75)

где знак минус поставлен в соответствии с принятой полярностью.

Для дырочного полупроводника такое выражение имеет вид

, (7.76)

Приведенная оценка дифференциальной термоЭДС для электронного германия с n=10²³м^-3приТ=300К даст величину порядка 10^-3В/к, что на три порядка больше чем, в металлах.

Увлечение электронов фононамипоявляется при низких температурах. Механизм эффекта заключается в следующем. При наличии градиента температуры в проводнике возникает термодиффузионное перемещение фононов от горячего конца к холодному со средней скоростью_ф.Электроны, которые рассеиваются на фононах, получают дополнительный импульс и сами перемещаются от горячего конца проводника к холодному, создавая термоЭДСU_ф. Расчет дифференциальной термоЭДС, обусловленной увлечением электронов фононами показал, что

, (7.77)

где τ_фиτ_е– среднее время релаксации фононов и электронов.

Применение эффекта Зеебека основано на преобразовании тепловой энергии в электрическую. Такое преобразование осуществляется в термоэлектрогенераторах, которые используют тепловую энергию солнечного излучения, радиоактивного распада, химических реакций. Достоинством термогенераторов является простота в эксплуатации, мобильность. Основной их недостаток – низкий КПД (~20%).

Эффект Зеебека широко используется для измерения температур. С помощью различных термопар измеряют температуру в диапазоне от -200°С до 2000°С. Достоинством термопар является относительная линейность их характеристик в рабочем диапазоне.

Кроме того, эффект Зеебека используют в устройствах функциональной теплоэлектроники, для генерации токовых импульсов (носителей информации) под действием тепловых импульсов.