2.2. Уравнение Шредингера. Волновая функция
Из вышеизложенного с очевидностью следует, что в микромире классическая механика неприменима. Ее место занимает квантовая механика – раздел теоретической физики, описывающий поведение микрочастиц.
Аналогом основного уравнения динамики для микромира является уравнение, постулированное Шредингером и носящее его имя. Для микрочастицы, находящейся в силовом поле и обладающей потенциальной энергией U(x,y,z,t), уравнение имеет следующий вид:
, (2.7)
где Ψ – волновая функция, в общем случае зависящая от координат и времени;
i– мнимая единица.
Волновая функция описывает поведение микрочастицы. Она является комплексной функцией, и физический смысл имеет не сама функция, а ее произведение на комплексно сопряженную функцию Ψ*. Такое произведение действительно и пропорционально вероятности того, что в моментtчастица находится в элементе объемаdV. Эта вероятностьω(x,y,z,t) определяется из выражения
w(x,y,z,t)dV= Ψ(x,y,z,t) Ψ*(x,y,z,t)dV. (2.8)
В соответствии со смыслом волновой функции, она должна быть непрерывной, однозначнойиконечнойво всех точках пространства, а также иметь непрерывную первую производную.
Для волновой функции справедливо условие нормировки
,
(2.9)
которое свидетельствует, что нахождение частицы в объеме V, если она находится в элементе этого объема, событие достоверное.
В общем случае потенциальная энергия микрочастицы зависит от координат и времени. Однако существует ряд задач для полей стационарного характера. В этих практически важных случаях потенциальная энергия не зависит от времени. Тогда выражение для волновой функции можно представить в виде произведения
Ψ(x,y,z,t) =ψ(x,y,z)φ(t). (2.10)
Для простоты выберем одномерный случай. Тогда можно записать
,
(2.11)
Ψ(x,t) =ψ(x)φ(t). (2.12)
Подставив (2.12) в (2.11) и разделив переменные, получим
,
(2.13)
Левая часть равенства является функцией только x, правая часть зависит только отt. Это возможно только тогда, когда каждая часть равна одной и той же постоянной величине. Можно показать, что эта постоянная есть полная энергия частицыE. Приравняем левую и правую части кEи преобразуем их. Тогда получим два уравнения для одномерного стационарного случая
,
(2.14)
.
(2.15)
Последнее уравнение легко интегрируется и дает решение в виде
,
(2.16)
где En– одно из собственных значений энергии частицы.
Из формулы (2.16) видно, что функция φn(t) являетсягармоническойс частотойνn=En/ћ.
Для того чтобы решить уравнение (2.14), необходимо определить вид функции потенциального поля U(x) и подставить его в (2.14). Тогда решение (2.13) будет иметь вид
Ψ(x,t)=
.
(2.17)
В данной главе приведены решения уравнения Шредингера для некоторых стационарных полей.
2.3. Свободный электрон. Фазовая и групповая скорости
Если считать частицу свободной и движущейся по оси x, тоU(x) = 0, уравнение Шредингера (2.14) примет вид
,
(2.18)
где k= 2π/λ– волновой вектор электрона;
E=p2/2m=ћ2k2 /2m– его энергия.
Решением уравнения (2.18) будет функция
ψ=ψ1+ψ2=Aexp(ikx) +Bexp(-ikx), (2.19)
где АиВ– постоянные коэффициенты.
С учетом (2.17) общее решение уравнения Шредингера будет иметь вид
Ψ(x,t) = A exp[i(kx-ωt)] + B exp[-i(kx+ωt)]. (2.20)
Последнее уравнение выражает суперпозицию двух плоских волн, распространяющихся в противоположных направлениях. Для частицы, движущейся по осиx,B=0. Для частицы, движущейся в противоположном направлении,A=0.
Для трехмерного случая решением уравнения Шредингера будет являться выражение
Ψ =
,
(2.21)
где
– радиус-вектор точки фронта волны.
Энергия свободной частицы будет равняться
,
(2.22)
для трехмерного случая
,
(2.23)
где kx,ky,kz– проекции волнового вектора на оси координат.
Выражения (2.22) и (2.23) показывают, что функция E(k) является непрерывной, т.е.энергетический спектр свободного электрона сплошной (рис. 2.1,а).
Поскольку микрочастица связана с плоской волной, имеет смысл рассмотреть вопрос о ее фазовой и групповой скоростях (п. 1.3).
В уравнении плоской волны, распространяющейся вдоль оси x, величинаφпредставляет собой фазу волны.
φ=k∙x-ω∙t, (2.24)
Напомним, что фазовая скорость υф– это скорость участка волны с постоянной фазой. Дифференцируя (2.24) с учетом постоянства фазы получим
.
(2.25)
Подставляя в (2.25) значения ωиk, можно записать
.
(2.26)
Анализ последнего выражения показывает, что фазовая скорость волн де Бройля зависит от их длины, т.е. имеет место эффект дисперсии.
Как отмечалось выше, в реальном случае частица представляет собой не монохроматическую волну, а волновой пакет, образованный двумя или более волнами, имеющими близкие значения длин и волновых векторов. Скорость этого пакета, групповая скорость гр
.
(2.27)
Подставив в последнее выражение значение k =m/ћи производнойdω/dk=ħk/m, получим:
гр =.
Последнее выражение показывает, что групповая скорость волн де Бройля равна скорости движения частицы.
В заключение рассмотрим вероятность нахождения свободного электрона в пространстве. Подставим в (2.8) выражение для плоской волны и получим w=const(рис. 2.1,б).
Это означает, что вероятность нахождения свободного электрона не зависит от координаты.
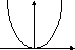
E
0k0х
a) б)
Рис. 2.1. Свободный электрон: а– энергетический спектр;б– вероятность нахождения